Vi ønsker, at denne maskine skal generere hele træningsdatasættet på egen hånd eller generere hele træningsdatasættet på baggrund af et stikord fra de oprindelige data. Hvis den f.eks. får et bitmap-billede med “SCI” som cue, vil den selv generere “ENCE” ud fra de vægte, den har lært.

For at få et billede af systemet for vores indre øje kan vi se på figur 5.

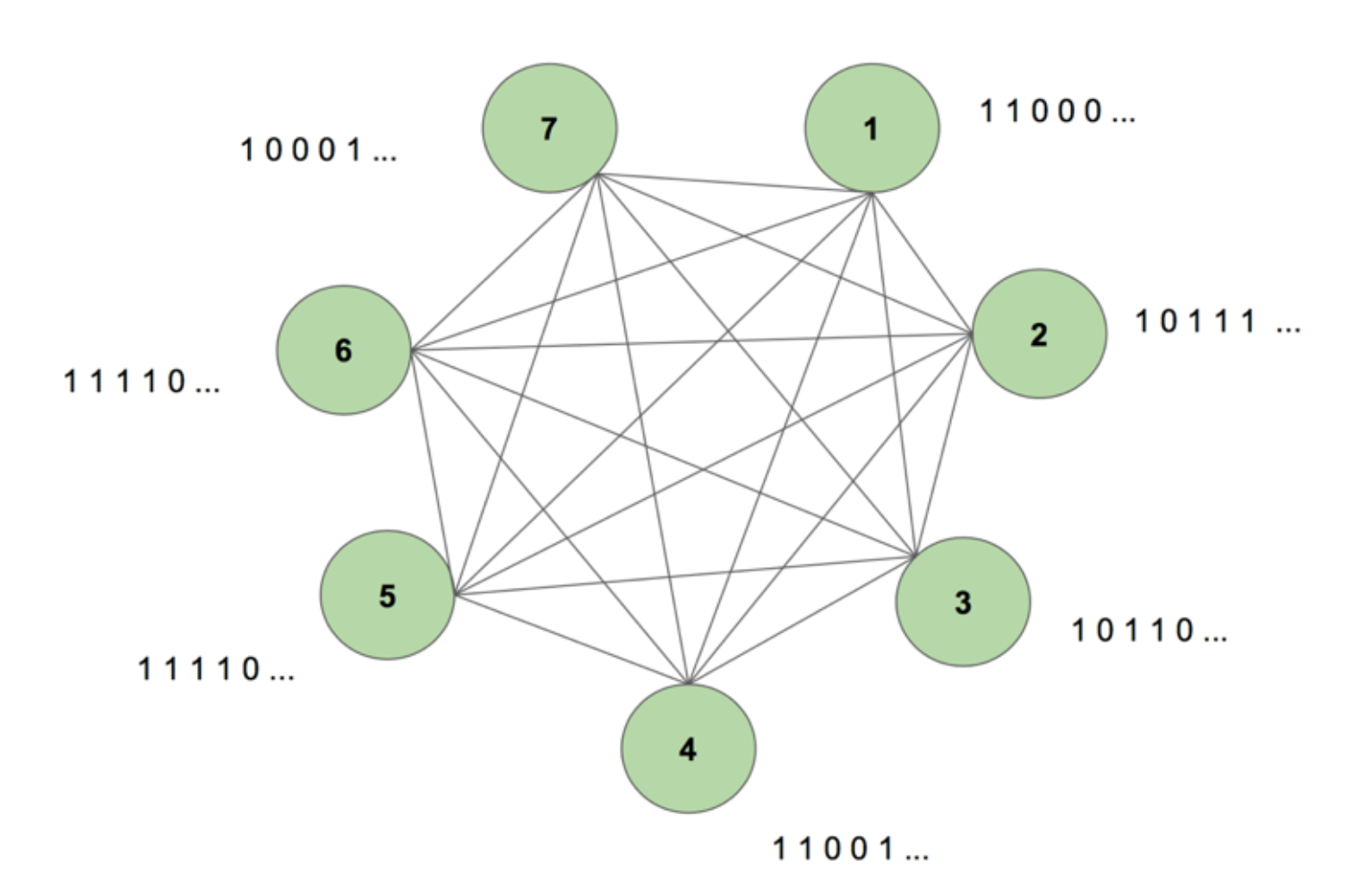
Maskinen indeholder syv knudepunkter. Et bitmap-billede på 7 x 35, der repræsenterer ordet SCIENCE, er målsekvensen. En træningsperiode består i at vise maskinen denne målsekvens én gang. Målet opdeles i 35 strimler med 7 værdier og føres ind i maskinen i samme rækkefølge som dets udseende i målet. Figur 5 viser, hvordan fem sådanne indtastningsstrimler ville se ud. Vi ser, at den første strimmel af vores bitmap, der består af alle 1’er, afspejles i den første værdi af indgangene i knudepunkterne. Det er sådan, vi indtaster værdier i maskinen under træningen.

Når vi først initialiserer maskinen med vilkårlige vægte og beder den om at generere en sekvens, skaber den noget helt tilfældigt. Efter at vi har trænet maskinen i 130.000 træningsperioder, er den i stand til at generere hele sekvensen af sig selv. Det betyder, at den under træningen optimerer sine vægte til at lære ikke blot biternes samtidige forekomst i et tidspas, men i hele sekvensen.

Magisk, ikke sandt? Men der er en solid logik bag dette magiske trick. Lad os løse mysteriet og se, hvorfor denne “Boltzmann-maskine med hukommelse” fungerer.

Dette er strukturen af en dynamisk Boltzmann-maskine (DyBM). I en Boltzmann-maskine indeholder en knude oplysninger om, hvilke knuder der aktiverer den på et bestemt tidspunkt. Dette gør den opmærksom på begivenheder, der forekommer sammen, men giver den ikke mulighed for at se tilbage og opbygge associationer på tværs af forskellige tidsskridt. Men i en DyBM repræsenterer forbindelserne mellem knuderne, hvordan knuderne interagerer over tid og ikke kun på et bestemt tidstrin. De DyBM letter dette ved at tilføje en ledningsforsinkelse mellem knuderne.

Med denne nye arkitektur har en knude oplysninger om, hvilke andre knuder der har katalyseret dens aktivering på et bestemt tidsskridt T = t gennem deres egne aktiviteter i de tidligere tidsskridt T = t – 1, T = t – 2 osv. Denne “hukommelse” tilføjes til en knude i form af en hukommelsesenhed. Denne enhed ændrer sandsynligheden for, at en knude er aktiveret på et hvilket som helst tidspunkt, afhængigt af de tidligere værdier af andre knuder og dens egne tilknyttede vægte.

Lad os antage, at vi har 2 knuder A og B. På et højt niveau udvider vi forestillingen om, at “neuroner, der skyder sammen, kobler sig sammen” på tværs af tidsdimensionen. For eksempel kan vi forestille os, at aktivering af A konsekvent fører til aktivering af B efter to tidsskridt. En ikke-dynamisk Boltzmann-maskine kan ikke opfange dette mønster, men med en DyBM kan jeg, eftersom værdien af A overføres til B efter en vis forsinkelse, opfange det mønster, at B = 1 på et tidspunkt efter A = 1. Nu vil sandsynligheden for, at B = 1 ved tidsskridt T = t variere ikke kun på grundlag af værdien af A ved T = t, men også på grundlag af værdierne af A ved T = t – 1, T = t – 2 osv. afhængigt af størrelsen af ledningsforsinkelsen mellem A og B.

Maskinen lagrer værdierne således, at nyere værdier tillægges større vægt, hvilket giver mening, da de nyeste dele af en tidsserie generelt er de mest informative om den seneste tendens. En DyBM lagrer disse oplysninger i de berettigede spor. Synaptic Eligibility Trace for B indeholder den vægtede sum af de værdier, der er nået frem til B fra A efter en vis ledningsforsinkelse. B’s neurale berettigelsesspor indeholder den vægtede sum af dets tidligere værdier.

I lighed med standard recurrent neural networks kan vi udfolde DyBM gennem tiden. Den udfoldede DyBM er en Boltzmann-maskine med et uendeligt antal enheder, der hver repræsenterer værdien af en knude på et bestemt tidspunkt.

Det er altså den dynamiske Boltzmann-maskine: en arkitektur, der har mulighed for at genskabe træningsdataene ikke blot på et tidspunkt, men på tværs af en sekvens af disse data.

DyBM’er er fascinerende, og den del, der følger, driver pointen videre.

Del 4: Faceoff mellem RNN-Gaussian-DyBM og LSTM

Alle de eksempler, vi har set indtil nu, har handlet om binære data (Bernoulli-fordeling). IBM-forskere gik et skridt videre og skabte et DyBM, der kunne modellere Gauss-fordelinger og gjorde det muligt for brugere som os at modellere tidsseriedata ved hjælp af DyBM og dets variationer.

For at kontrollere effektiviteten af et DyBM kørte jeg nogle tests, hvor jeg sammenlignede et RNN-Gaussian-DyBM (et DyBM med RNN-lag) og det nuværende state-of-the-art, Long Short-Term Memory Neural Network. Resultaterne var spændende. Du er velkommen til at køre disse tests på egen hånd, baseret på det script, der er tilgængeligt her.

Lad os se, hvordan et DyBMM sammenligner sig med et LSTM på en tidsserie-brugstilfælde.

Brugstilfælde:

Vi vil bruge data, der indeholder det månedlige solpletnummer beregnet i et laboratorium i Zürich fra år 1749 til 1983. Dataene er open source og tilgængelige fra Datamarket – Monthly sunspot number, Zurich, 1749-1983.

Først skal vi se, hvordan LSTM’en klarede sig.

LSTM

• Arkitektur: LSTM

  LSTM

  • Arkitektur: LSTM Dimension = 10.
  • Præstation over 10 epoker: Gennemsnitlig testscore LSTM = 0,08877 RMSE
  • Per epok tid til at lære: 8.689403 sek.

  

  Nu vil vi se, hvordan en RNN-Gaussian-DyBM klarede sig på de samme data.

  Borg dig selv, dette bliver en meget interessant opdagelsesrejse … Klar?

  RNNN-Gaussian-DyBM

  • Arkitektur: RNN Dimension = 10 og inputdimension = 1
  • Præstation over 10 epoker: Gennemsnitlig testscore LSTM = 0,07848 RMSE
  • Per epok tid til at lære: 0,90547 sek.

  

  I dette tilfælde kører RNN-Gaussian-DyBM ikke blot 10 gange hurtigere, den giver også en bedre ydeevne.

  Når vi skalerer antallet af epokeringer for de to modeller, øges tidsforskellen mellem træningen af disse to modeller drastisk. DyBM-reaktionstiden er meget hurtigere, så træne – teste – implementere cyklusen skrumper, og du kan forbedre modellerne meget hurtigere.

  Men vi har endnu ikke diskuteret den bedste del af DyBM’erne: Du kan fremskynde dem med GPU-acceleration. En DyBM, der kører på en GPU på IBM Watson Studio Local med Power AI IBM Cloud Service, kan lave forudsigelser for over 2.000 tidsserier, hver med en længde på mere end 500, på mindre end 10 sekunder pr. epoch. I modsætning hertil vil det tage lidt over 30 minutter for en DyBM, der kører på CPU, at udføre den samme opgave. Sammenlign dette resultat med ydelsen for en LSTM på CPU fra det foregående eksempel. Forestil dig blot den beregningskraft, som dette giver. Se her for at få flere oplysninger om acceleration af DyBM’er med GPU’er. Det er værd at bemærke, at du også kan accelerere LSTM’er med GPU’er, og sammenligningen af ydeevnen mellem en accelereret DyBM og en accelereret LSTM vil variere.

  Næste gang du vil løse et tidsserieproblem, så giv Dynamic Boltzmann Machines en chance. Overvej at starte med IBM Research Tokyo GitHub-repositoriet for Dynamic Boltzmann Machines, som du kan finde her.

  Se nedenfor for yderligere dybdegående forskning om energibaserede modeller, Boltzmann-maskiner og dynamiske Boltzmann-maskiner:

  • A Tutorial on Energy-Based Learning – Yann LeCun, Sumit Chopra, Sumit Chopra, Raia Hadsell, Marc’Aurelio Ranzato, og Fu Jie Huang
  • Boltzmann-maskiner – Geoffrey Hinton
  • Boltzmann-maskiner og energibaserede modeller – Takayuki Osogami (IBM Research – Tokyo)
  • Syv neuroner, der husker sekvenser af alfabetiske billeder via spike-timing-afhængig plasticitet – Takayuki Osogami og Makoto Otsuka
  • Non-lineære dynamiske Boltzmann-maskiner til forudsigelse af tidsserier – Sakyasingha Dasgupta og Takayuki Osogami (IBM Research – Tokyo)