Nous voulons que cette machine génère l’ensemble des données d’entraînement par elle-même ou qu’elle génère l’ensemble des données d’entraînement en fonction d’un indice provenant des données originales. Par exemple, étant donné une image bitmap cue contenant « SCI », elle générerait « ENCE » par elle-même à partir des poids qu’elle a appris.

Pour avoir une image du système dans notre esprit, considérons la figure 5.

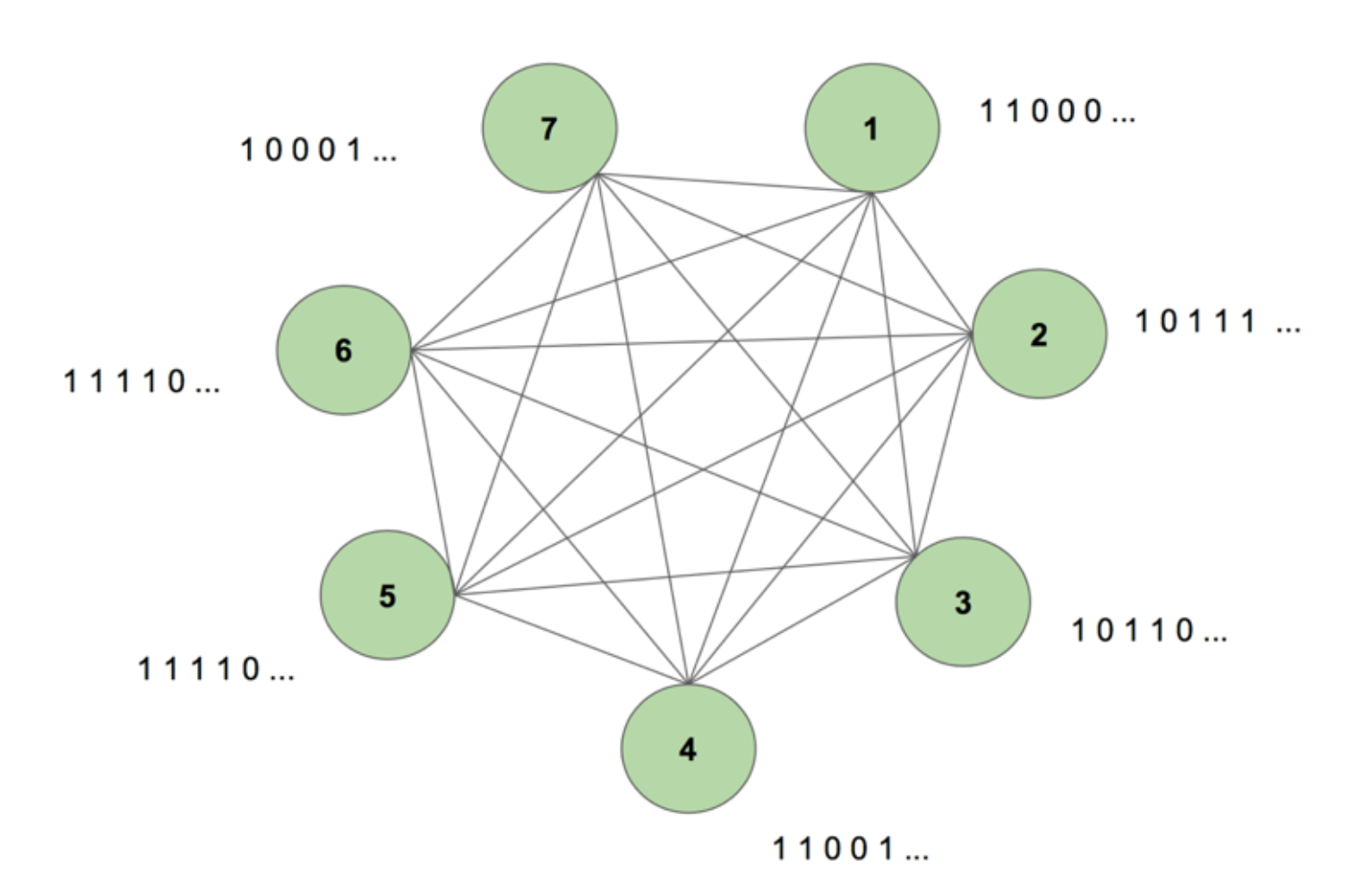
La machine contient sept nœuds. Une image bitmap de 7 par 35 représentant le mot SCIENCE est la séquence cible. Une période d’entraînement consiste à montrer une fois à la machine cette séquence cible. La cible est décomposée en 35 bandes de 7 valeurs et introduite dans la machine dans le même ordre que son apparition dans la cible. La figure 5 montre à quoi ressembleraient cinq de ces bandes d’entrée. Nous voyons que la première bande de notre bitmap, composée de tous les 1, se reflète dans la première valeur des entrées des nœuds. C’est ainsi que nous entrons des valeurs dans la machine pendant l’entraînement.

Lorsque nous initialisons d’abord la machine avec des poids arbitraires et que nous lui demandons de générer une séquence, elle crée quelque chose de complètement aléatoire. Après avoir entraîné la machine pendant 130 000 périodes d’entraînement, elle est capable de générer la séquence entière par elle-même. Cela signifie que, pendant l’entraînement, elle optimise ses poids pour apprendre non seulement la cooccurrence des bits à un moment donné, mais sur l’ensemble d’une séquence.

Magique, n’est-ce pas ? Mais il y a une logique solide derrière ce tour de magie. Déchiffrons le mystère et voyons pourquoi cette « machine de Boltzmann avec mémoire » fonctionne.

Voici la structure d’une machine de Boltzmann dynamique (DyBM). Dans une machine de Boltzmann, un nœud contient des informations sur les nœuds qui l’activent à un moment donné. Cela lui permet d’être conscient des événements qui se produisent ensemble, mais ne lui donne pas la possibilité de regarder en arrière et de construire des associations à travers différents pas de temps. Mais dans un DyBM, les connexions entre les nœuds représentent la manière dont les nœuds interagissent dans le temps, et pas seulement à un moment donné. Le DyBM facilite cela en ajoutant un délai de conduction entre les nœuds.

Avec cette nouvelle architecture, un nœud possède des informations sur les autres nœuds qui ont catalysé son activation à un certain pas de temps T = t grâce à leurs propres activités dans les pas de temps passés T = t – 1, T = t – 2, et ainsi de suite. Cette « mémoire » est ajoutée à un nœud sous la forme d’une unité de mémoire. Cette unité modifie la probabilité qu’un nœud soit activé à tout moment, en fonction des valeurs précédentes des autres nœuds et de ses propres poids associés.

Considérons que nous avons 2 nœuds A et B. A un haut niveau, nous étendons la notion que « les neurones qui tirent ensemble, se connectent ensemble » à travers la dimension du temps. Par exemple, imaginons que l’activation de A entraîne systématiquement l’activation de B après deux pas de temps. Une machine de Boltzmann non dynamique ne peut pas capturer ce modèle, mais avec une machine de DyBM, puisque la valeur de A se déplace vers B après un certain délai, je peux capturer le modèle selon lequel B = 1 quelque temps après A = 1. Maintenant, la probabilité que B = 1 au pas de temps T = t variera en fonction non seulement de la valeur de A à T = t, mais aussi des valeurs de A à T = t – 1, T = t – 2, et ainsi de suite, selon la quantité de retard de conduction entre A et B.

La machine stocke les valeurs de sorte que les valeurs récentes ont un poids plus élevé, ce qui est logique puisqu’en général les parties les plus récentes d’une série chronologique sont les plus informatives sur la dernière tendance. Un DyBM stocke ces informations dans les traces d’éligibilité. La trace d’admissibilité synaptique de B contient la somme pondérée des valeurs qui ont atteint B depuis A après un certain délai de conduction. La trace d’admissibilité neuronale de B contient la somme pondérée de ses valeurs passées.

Similairement aux réseaux neuronaux récurrents standard, nous pouvons déplier le DyBM dans le temps. La DyBM dépliée est une machine de Boltzmann ayant un nombre infini d’unités, chacune représentant la valeur d’un nœud à un moment particulier.

C’est donc la machine de Boltzmann dynamique : une architecture qui a le pouvoir de recréer les données d’entraînement non seulement à un moment donné, mais à travers une séquence de ces données.

Les DyBM sont fascinantes, et la partie qui suit enfonce le clou.

Partie 4 : Face-à-face entre RNN-Gaussien-DyBM et LSTM

Tous les exemples que nous avons vus jusqu’à présent portaient sur des données binaires (distribution de Bernoulli). Les chercheurs d’IBM sont allés un peu plus loin et ont créé un DyBM capable de modéliser des distributions gaussiennes et ont permis à des utilisateurs comme nous de modéliser des données de séries temporelles à l’aide du DyBM et de ses variantes.

Pour vérifier l’efficacité d’un DyBM, j’ai effectué des tests comparant un RNN-Gaussien-DyBM (un DyBM avec une couche RNN) et l’état actuel de la technique, le réseau neuronal à mémoire à long court terme. Les résultats sont passionnants. N’hésitez pas à exécuter ces tests sur votre propre, sur la base du script disponible ici.

Voyons comment un DyBM se compare à un LSTM sur un cas d’utilisation de séries temporelles.

Cas d’utilisation : Prédire la valeur du prochain nombre de taches solaires.

Nous allons utiliser des données contenant le nombre mensuel de taches solaires calculé dans un laboratoire à Zurich de l’année 1749 à 1983. Les données sont open source et disponibles sur Datamarket – Monthly sunspot number, Zurich, 1749-1983.

D’abord, voyons comment le LSTM s’est comporté.

LSTM

• Architecture : LSTM Dimension = 10,
• Performances sur 10 époques : Moyenne des résultats du test LSTM = 0,08877 RMSE
• Par époque temps d’apprentissage : 8,689403 sec.

Nous allons maintenant voir comment un RNN-Gaussien-DyBM s’est comporté sur les mêmes données.

Attachez-vous, cela va être un voyage de découverte très intéressant… Prêt ?

RNN-Gaussien-DyBM

• Architecture : RNN Dimension = 10 et Dimension d’entrée = 1
• Performances sur 10 époques : Moyenne des résultats du test LSTM = 0,07848 RMSE
• Temps d’apprentissage par époque : 0,90547 sec.

Non seulement le RNN-Gaussien-DyBM s’exécute 10 fois plus vite dans ce cas, mais il offre également de meilleures performances.

A mesure que nous mettons à l’échelle le nombre d’époques pour les deux modèles, la différence de temps entre l’entraînement de ces deux modèles augmente drastiquement. Le temps de réponse du DyBM est beaucoup plus rapide, donc le cycle former – tester – déployer se réduit et vous pouvez améliorer les modèles beaucoup plus rapidement.

Mais nous n’avons pas encore abordé la meilleure partie des DyBM : Vous pouvez les accélérer avec l’accélération GPU. Un DyBM exécuté sur un GPU sur IBM Watson Studio Local avec Power AI IBM Cloud Service peut faire des prédictions pour plus de 2000 séries temporelles, chacune d’une longueur supérieure à 500, en moins de 10 secondes par époque. En revanche, un DyBM fonctionnant sur le CPU mettra un peu plus de 30 minutes pour effectuer la même tâche. Comparez ce résultat avec les performances d’un LSTM sur le CPU dans l’exemple précédent. Imaginez la puissance de calcul que cela procure. Voir ici pour plus d’informations sur l’accélération des DyBMs avec les GPUs. Il convient de noter que vous pouvez également accélérer les LSTM avec les GPU, et la comparaison des performances entre une DyBM accélérée et un LSTM accéléré variera.

La prochaine fois que vous voudrez résoudre un problème de séries temporelles, essayez les machines de Boltzmann dynamiques. Envisagez de commencer par le dépôt GitHub d’IBM Research Tokyo pour les machines de Boltzmann dynamiques, que vous pouvez trouver ici.

Voir ci-dessous pour des recherches approfondies supplémentaires sur les modèles basés sur l’énergie, les machines de Boltzmann et les machines de Boltzmann dynamiques :

• Un tutoriel sur l’apprentissage basé sur l’énergie – Yann LeCun, Sumit Chopra, Raia Hadsell, Marc’Aurelio Ranzato, et Fu Jie Huang
• Machines de Boltzmann – Geoffrey Hinton
• Machines de Boltzmann et modèles basés sur l’énergie – Takayuki Osogami (IBM Research – Tokyo)
• Sept neurones mémorisant des séquences d’images alphabétiques via une plasticité dépendante du timing des spikes-.timing dependent plasticity – Takayuki Osogami and Makoto Otsuka
• Nonlinear Dynamic Boltzmann Machines for Time-Series Prediction – Sakyasingha Dasgupta and Takayuki Osogami (IBM Research – Tokyo)

.