Vi vill att maskinen ska generera hela träningsdatasetet på egen hand eller generera hela träningsdatasetetet baserat på en ledtråd från de ursprungliga uppgifterna. Till exempel, om den får en bitmappbild som innehåller ”SCI” skulle den generera ”ENCE” på egen hand utifrån de vikter som den har lärt sig.

För att få en bild av systemet i vårt sinne kan vi betrakta figur 5.

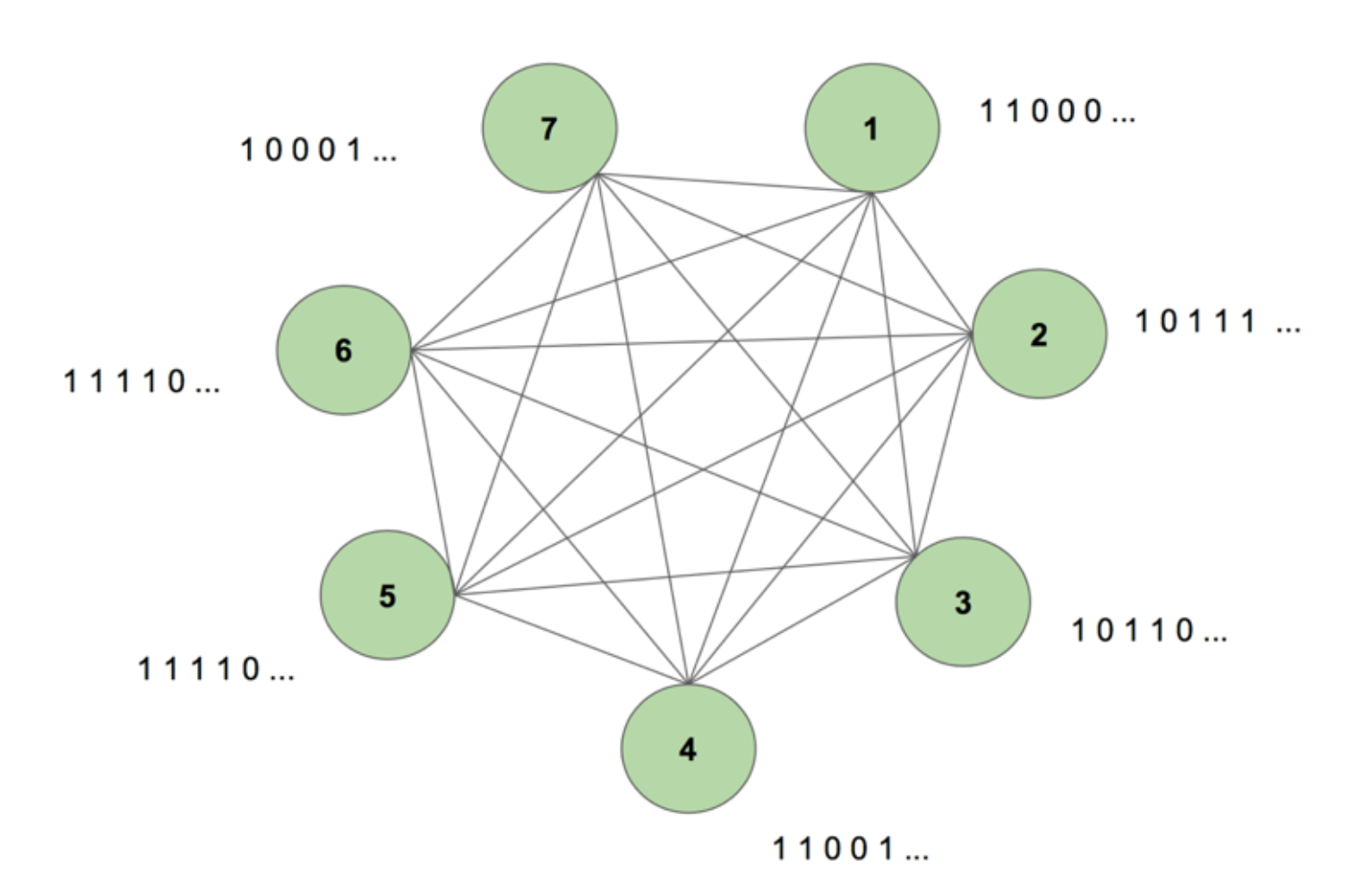
Maskinen innehåller sju noder. En bitmappbild på 7 x 35 som representerar ordet SCIENCE är målsekvensen. En träningsperiod består av att visa maskinen denna målsekvens en gång. Målet delas upp i 35 remsor med 7 värden och matas in i maskinen i samma ordning som dess utseende i målet. Figur 5 visar hur fem sådana inmatningsremsor skulle se ut. Vi ser att den första remsan i vår bitmapp, som består av alla 1:or, återspeglas i det första värdet i nodernas ingångar. Detta är hur vi matar in värden i maskinen under träningen.

När vi först initialiserar maskinen med godtyckliga vikter och ber den generera en sekvens skapar den något helt slumpmässigt. Efter att vi tränat maskinen i 130 000 träningsperioder kan den generera hela sekvensen på egen hand. Detta innebär att den under träningen optimerar sina vikter för att lära sig inte bara bitarnas samtidiga förekomst i en tidsperiod, utan över en hel sekvens.

Magiskt, eller hur? Men det finns solid logik bakom detta magiska trick. Låt oss avslöja mysteriet och se varför denna ”Boltzmannmaskin med minne” fungerar.

Detta är strukturen hos en dynamisk Boltzmannmaskin (DyBM). I en Boltzmannmaskin innehåller en nod information om vilka noder som aktiverar den vid en viss tidpunkt. Detta gör den medveten om händelser som inträffar tillsammans, men ger den inte möjlighet att se tillbaka och bygga upp associationer över olika tidsperioder. Men i en DyBM representerar kopplingarna mellan noderna hur noderna interagerar över tiden, inte bara vid ett visst tidsintervall. De DyBM underlättar detta genom att lägga till en ledningsfördröjning mellan noderna.

Med denna nya arkitektur har en nod information om vilka andra noder som katalyserat dess aktivering vid ett visst tidssteg T = t genom deras egna aktiviteter i de tidigare tidsstegen T = t – 1, T = t – 2 och så vidare. Detta ”minne” läggs till en nod i form av en minnesenhet. Denna enhet ändrar sannolikheten för att en nod aktiveras vid varje ögonblick, beroende på tidigare värden för andra noder och dess egna associerade vikter.

Låt oss betrakta att vi har två noder A och B. På en hög nivå utvidgar vi föreställningen om att ”neuroner som skjuter tillsammans, kopplar ihop” över tidsdimensionen. Tänk dig till exempel att aktivering av A konsekvent leder till aktivering av B efter två tidssteg. En icke-dynamisk Boltzmann-maskin kan inte fånga detta mönster, men med en DyBM kan jag fånga mönstret att B = 1 någon gång efter att A = 1, eftersom värdet av A överförs till B efter en viss fördröjning. Nu kommer sannolikheten att B = 1 vid tidssteget T = t att variera inte bara baserat på värdet av A vid T = t, utan också på värdena av A vid T = t – 1, T = t – 2 och så vidare, beroende på hur stor ledningsfördröjningen mellan A och B är.

Maskinen lagrar värdena så att de senaste värdena ges högre vikt, vilket är vettigt eftersom de senaste delarna av en tidsserie generellt sett är de mest informativa om den senaste trenden. En DyBM lagrar denna information i de stödberättigande spåren. Synaptic Eligibility Trace of B innehåller den viktade summan av de värden som har nått B från A efter en viss ledningsfördröjning. Det neurala spåret för B:s berättigande innehåller den viktade summan av dess tidigare värden.

I likhet med vanliga återkommande neurala nätverk kan vi veckla ut DyBM genom tiden. Den utvikta DyBM är en Boltzmann-maskin med ett oändligt antal enheter, som var och en representerar värdet av en nod vid en viss tidpunkt.

Det här är alltså den dynamiska Boltzmann-maskinen: en arkitektur som har förmågan att återskapa träningsdata, inte bara vid en tidpunkt, utan över en sekvens av dessa data.

DyBMs är fascinerande, och delen som följer driver poängen hem.

Del 4: Faceoff mellan RNN-Gaussian-DyBM och LSTM

Alla exempel som vi har sett hittills har handlat om binära data (Bernoulli-fördelning). IBM:s forskare gick ett steg längre och skapade ett DyBM som kunde modellera Gaussiska fördelningar och gjorde det möjligt för användare som oss att modellera tidsseriedata med hjälp av DyBM och dess varianter.

För att kontrollera effektiviteten hos ett DyBM utförde jag några tester där jag jämförde ett RNN-Gaussian-DyBM (ett DyBM med RNN-skikt) och den nuvarande toppmoderna tekniken, Long Short-Term Memory Neural Network. Resultaten var spännande. Kör gärna dessa tester på egen hand, baserat på det skript som finns här.

Låt oss se hur ett DyBM jämför sig med ett LSTM på ett användningsfall för tidsserier.

Användningsfall:

Vi kommer att använda data som innehåller det månatliga solfläcksantalet beräknat i ett labb i Zürich från år 1749 till 1983. Datan är öppen källkod och tillgänglig från Datamarket – Monthly sunspot number, Zurich, 1749-1983.

Först ska vi se hur LSTM presterade.

LSTM

• Arkitektur: LSTM Dimension = 10.
• Prestanda över 10 epoker: Medelvärde för testresultat LSTM = 0,08877 RMSE
• Per epok tid för inlärning: LSTM = 0,08877 RMSE
• Per epok tid för inlärning: 8.689403 sek.

Nu ska vi se hur en RNN-Gaussian-DyBM presterade på samma data.

Var beredd, detta kommer att bli en mycket intressant upptäcktsresa… Redo?

RNNN-Gaussian-DyBM

• Arkitektur: RNN-dimension = 10 och indata-dimension = 1
• Prestanda över 10 epoker: Medelvärde för testresultat LSTM = 0,07848 RMSE
• Tid för inlärning per epok: 1,07848 RMSE
• Per epok:

RN-Na RNN-Gaussian-DyBM körs inte bara tio gånger snabbare i det här fallet, utan ger också bättre prestanda.

När vi skalar antalet epoker för de två modellerna ökar tidsskillnaden mellan träningen av dessa två modeller drastiskt. DyBM:s svarstid är mycket snabbare, så cykeln träna – testa – distribuera krymper och du kan förbättra modellerna mycket snabbare.

Men vi har ännu inte diskuterat det bästa med DyBM: Du kan snabba upp dem med GPU-acceleration. En DyBM som körs på en GPU på IBM Watson Studio Local med Power AI IBM Cloud Service kan göra förutsägelser för över 2 000 tidsserier, var och en med en längd på mer än 500, på mindre än 10 sekunder per epok. En DyBM som körs på CPU tar däremot lite mer än 30 minuter för att göra samma uppgift. Jämför det här resultatet med prestandan för en LSTM på CPU från föregående exempel. Föreställ dig bara vilken beräkningskraft detta ger. Se här för mer information om att accelerera DyBMs med GPU:er. Det är värt att notera att du också kan accelerera LSTMs med GPU:er, och prestandavärderingen mellan en accelererad DyBM och en accelererad LSTM kommer att variera.

Nästa gång du vill lösa ett tidsserieproblem kan du ge Dynamic Boltzmann Machines ett försök. Överväg att börja med IBM Research Tokyos GitHub-arkiv för Dynamic Boltzmann Machines, som du hittar här.

Se nedan för ytterligare fördjupad forskning om energibaserade modeller, Boltzmannmaskiner och dynamiska Boltzmannmaskiner:

• A Tutorial on Energy-Based Learning – Yann LeCun, Sumit Chopra, Raia Hadsell, Marc’Aurelio Ranzato, och Fu Jie Huang
• Boltzmannmaskiner – Geoffrey Hinton
• Boltzmannmaskiner och energibaserade modeller – Takayuki Osogami (IBM Research – Tokyo)
• Sju neuroner som memorerar sekvenser av alfabetiska bilder via spike-timing dependent plasticity – Takayuki Osogami and Makoto Otsuka
• Nonlinear Dynamic Boltzmann Machines for Time-Series Prediction – Sakyasingha Dasgupta and Takayuki Osogami (IBM Research – Tokyo)

>