Queremos que esta máquina gere todo o conjunto de dados de treinamento por si só ou que gere todo o conjunto de dados de treinamento com base em um taco dos dados originais. Por exemplo, dada uma imagem de bitmap de taco contendo “SCI”, ela geraria “ENCE” por si só a partir dos pesos que aprendeu.
Para obter uma imagem do sistema no olho da nossa mente, considere a Figura 5.
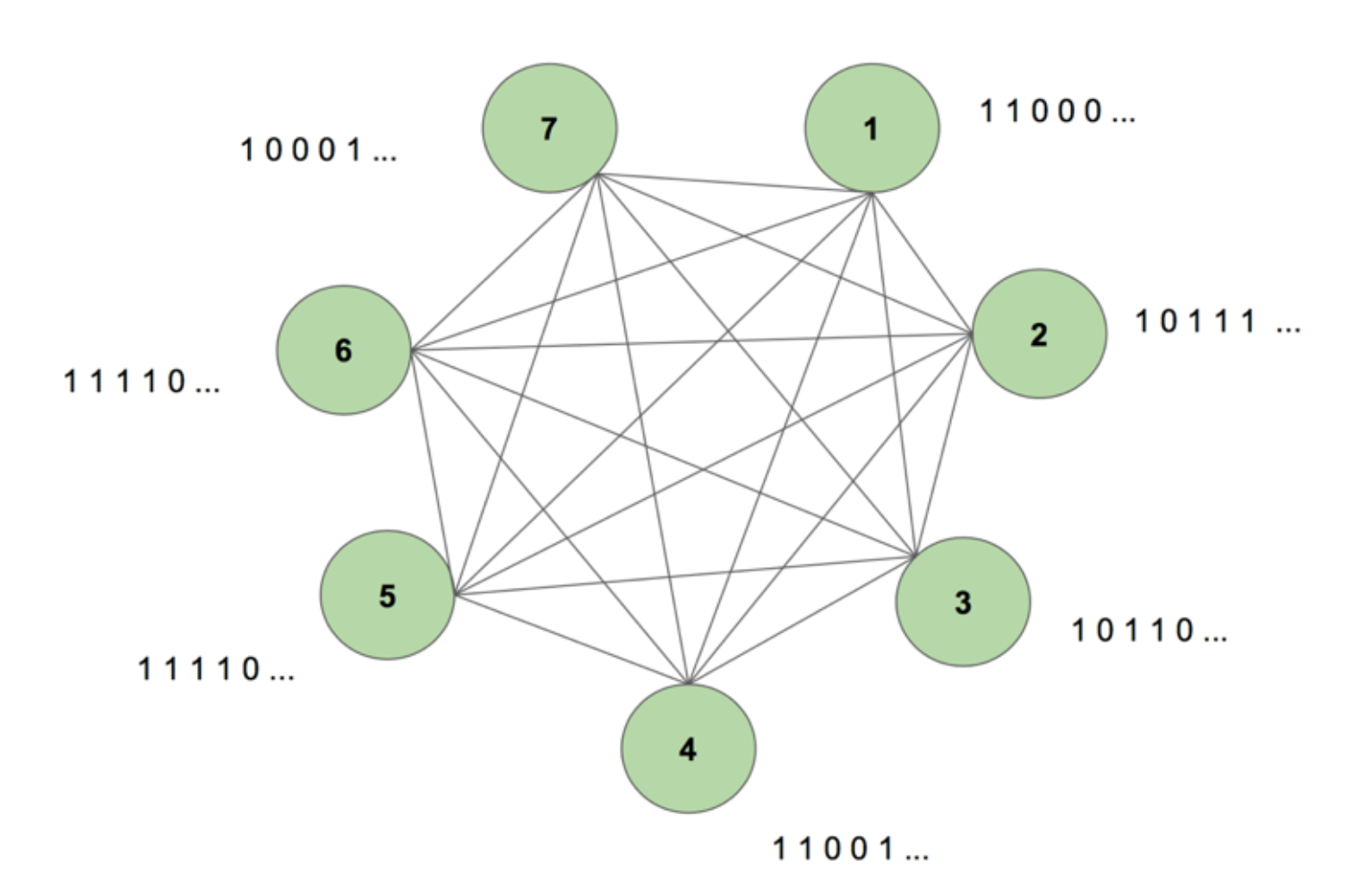
A máquina contém sete nós. Uma imagem 7 por 35 bitmap representando a palavra CIÊNCIA é a sequência alvo. Um período de treinamento consiste em mostrar à máquina esta seqüência alvo uma vez. O alvo é decomposto em 35 tiras de 7 valores e introduzido na máquina na mesma sequência que a sua aparência no alvo. A Figura 5 mostra como seriam cinco dessas tiras de entrada. Vemos que a primeira tira do nosso bitmap, composta por todos os 1s, é refletida no primeiro valor das entradas dos nós. Isto é como nós inserimos valores na máquina durante o treinamento.
Quando inicializamos a máquina com pesos arbitrários e pedimos a ela para gerar uma seqüência, ela cria algo completamente aleatório. Depois de treinarmos a máquina durante 130.000 períodos de treino, ela é capaz de gerar a sequência inteira por si mesma. Isto significa que durante o treinamento, ele otimiza seus pesos para aprender não apenas a co-ocorrência de bits em uma única etapa de tempo, mas em toda uma seqüência.
Magical, não é? Mas há uma lógica sólida por detrás deste truque de magia. Vamos desvendar o mistério e ver porque esta “Máquina Boltzmann com Memória” funciona.
>

>
Esta é a estrutura de uma Máquina Boltzmann Dinâmica (DyBM). Em uma Máquina Boltzmann, um nó contém informações sobre quais nós a ativam em um determinado momento. Isto torna-o consciente dos eventos que ocorrem em conjunto, mas não lhe dá a capacidade de olhar para trás e construir associações através de diferentes períodos de tempo. Mas em um DyBM as conexões entre os nós representam como os nós interagem ao longo do tempo, e não apenas em uma determinada faixa de tempo. O DyBM facilita isso ao adicionar um atraso de condução entre os nós.
Com essa nova arquitetura, um nó tem informações sobre quais outros nós catalisaram sua ativação em alguma hora T = t através de suas próprias atividades em temporizações anteriores T = t – 1, T = t – 2, e assim por diante. Esta “memória” é adicionada a um nó sob a forma de uma unidade de memória. Esta unidade altera a probabilidade de um nó ser ativado a qualquer momento, dependendo dos valores anteriores de outros nós e seus próprios pesos associados.
Consideremos que temos 2 nós A e B. Em um nível alto, estamos estendendo a noção de que “neurônios que disparam juntos, conectam-se” através da dimensão do tempo. Por exemplo, imagine que a ativação de A leva consistentemente à ativação de B após duas etapas de tempo. Uma Máquina Boltzmann não dinâmica não captura este padrão, mas com um DyBM, já que o valor de A viaja para B após algum atraso, posso capturar o padrão que B = 1 algum tempo depois de A = 1. Agora a probabilidade de que B = 1 no tempo T = t irá variar com base não só no valor de A em T = t, mas também nos valores de A em T = t – 1, T = t – 2, e assim por diante, dependendo da quantidade de atraso de condução entre A e B.
A máquina armazena os valores para que os valores recentes recebam maior peso, o que faz sentido já que em geral as partes mais recentes de uma série temporal são as mais informativas sobre a última tendência. A DyBM armazena esta informação nos traços de elegibilidade. O traço de elegibilidade sináptico de B contém a soma ponderada dos valores que chegaram a B de A após algum atraso na condução. O Rastro de Elegibilidade Neural de B contém a soma ponderada de seus valores passados.
Similar às redes neurais recorrentes padrão, podemos desdobrar o DyBM ao longo do tempo. O DyBM desdobrado é uma Máquina Boltzmann com um número infinito de unidades, cada uma representando o valor de um nó em um determinado momento.
Então, esta é a Máquina Boltzmann Dinâmica: uma arquitetura que tem o poder de recriar os dados de treinamento não apenas em um ponto no tempo, mas através de uma seqüência desses dados.
DyBMs são fascinantes, e a parte que se segue conduz o ponto para casa.
Parte 4: Faceoff Between RNNN-Gaussian-DyBM and LSTM
Todos os exemplos que vimos até agora lidaram com dados binários (Distribuição Bernoulli). Os pesquisadores da IBM foram um passo além e criaram um DyBM que podia modelar distribuições Gaussianas e possibilitou que usuários como nós modelassem dados da série temporal usando o DyBM e suas variações.
Para verificar a eficiência de um DyBM, fiz alguns testes comparando um RNNN-Gaussian-DyBM (um DyBM com camada RNN) e a rede neural de memória de curto prazo de última geração. Os resultados foram empolgantes. Sinta-se livre para executar esses testes por conta própria, baseado no script disponível aqui.
Vejamos como um DyBM se compara a um LSTM em um caso de uso de série temporal.
Use Case: Preveja o valor do próximo número de mancha solar.
Usaremos dados contendo o Número Mensal de Mancha Solar calculado num laboratório em Zurique do ano de 1749 a 1983. Os dados são de código aberto e estão disponíveis no Datamarket – Número mensal de manchas solares, Zurique, 1749-1983.
Primeiro, vamos ver como o LSTM funcionava.
LSTM
- Arquitectura: LSTM Dimensão = 10,
- Desempenho durante 10 épocas: Pontuação média do teste LSTM = 0,08877 RMSE
- Por época para aprender: 8,689403 seg.

>
Agora veremos como um RNNN-Gaussiano-DyBM se comportou com os mesmos dados.
Brace-se, esta vai ser uma viagem de descoberta muito interessante… Pronto?
RNN-Gaussie-DyBM
- Arquitectura: Dimensão RNN = 10 e Dimensão de Entrada = 1
- Desempenho em 10 épocas: Pontuação Média do Teste LSTM = 0,07848 RMSE
- Por época para aprender: 0,90547 seg.

Não só o RNNN-Gaussio-DyBM funciona 10 vezes mais rápido neste caso, como também oferece um melhor desempenho.
Como escalamos o número de épocas para os dois modelos, a diferença de tempo entre os treinos destes dois modelos aumenta drasticamente. O tempo de resposta do DyBM é muito mais rápido, então o trem – teste – implantar ciclo encolhe e você pode melhorar os modelos muito mais rápido.
Mas ainda não discutimos a melhor parte sobre os DyBMs: Você pode acelerá-los com a aceleração da GPU. Um DyBM rodando em uma GPU no IBM Watson Studio Local com Power AI IBM Cloud Service pode fazer previsões para mais de 2000 séries temporais, cada uma com mais de 500, em menos de 10 segundos por época. Em contraste, um DyBM rodando em um CPU levará um pouco mais de 30 minutos para fazer a mesma tarefa. Compare este resultado com o desempenho de um LSTM na CPU do exemplo anterior. Imagine só a potência computacional que isso proporciona. Veja aqui para mais informações sobre como acelerar DyBMs com GPUs. Vale notar que você também pode acelerar LSTMs com GPUs, e a comparação de performance entre um DyBM acelerado e um LSTM acelerado irá variar.
Próxima vez que você quiser resolver um problema de série de tempo, dê uma tentativa às Máquinas Dinâmicas Boltzmann. Considere começar com o repositório IBM Research Tokyo GitHub para Dynamic Boltzmann Machines, que você pode encontrar aqui.
Veja abaixo para uma pesquisa adicional aprofundada sobre Modelos Baseados em Energia, Máquinas Boltzmann e Máquinas Boltzmann Dinâmicas:
- A Tutorial sobre Aprendizagem Baseada em Energia – Yann LeCun, Sumit Chopra, Raia Hadsell, Marc’Aurelio Ranzato, e Fu Jie Huang
- Boltzmann Machines – Geoffrey Hinton
- Boltzmann Machines and Energy-Based Models – Takayuki Osogami (IBM Research – Tokyo)
- Seven neurons memorizing sequences of alfabetical images via spike-plasticidade dependente do tempo – Takayuki Osogami e Makoto Otsuka
- Nonlinear Dynamic Boltzmann Machines for Time-Series Prediction – Sakyasingha Dasgupta e Takayuki Osogami (IBM Research – Tokyo)