We willen dat deze machine de hele trainingsdataset zelf genereert of de hele trainingsdataset genereert op basis van een cue uit de originele data. Bijvoorbeeld, gegeven een cue bitmap beeld dat “SCI” bevat, zou het zelf “ENCE” genereren op basis van de gewichten die het heeft geleerd.

Om een beeld te krijgen van het systeem in ons geestesoog, bekijk figuur 5.

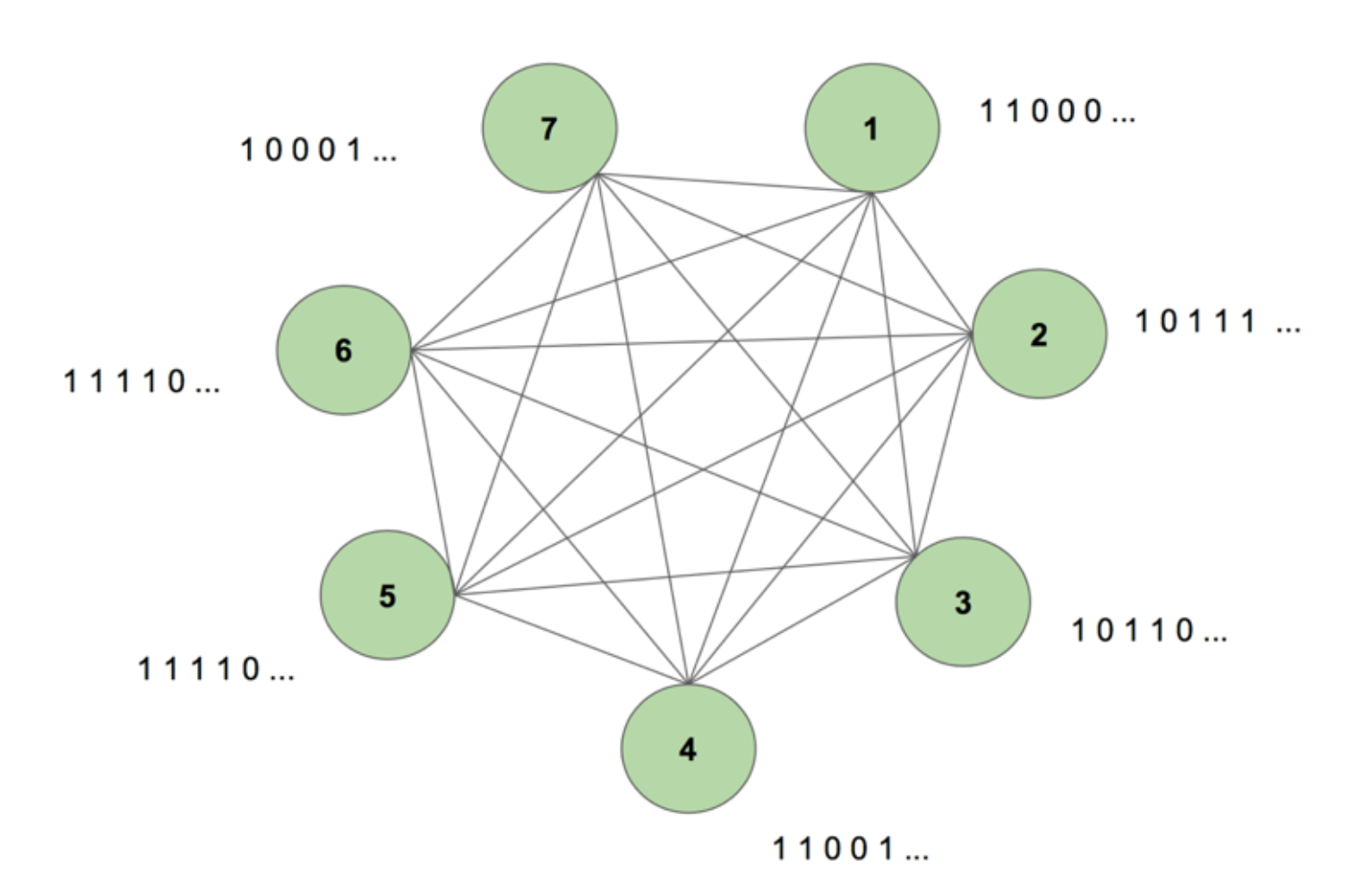
De machine bevat zeven knooppunten. De doelsequentie is een bitmap-afbeelding van 7 bij 35 die het woord SCIENCE weergeeft. Een trainingsperiode bestaat uit het eenmaal tonen van deze doelsequentie aan de machine. Het doel wordt opgesplitst in 35 stroken van 7 waarden en aan de machine ingevoerd in dezelfde volgorde als waarin ze in het doel voorkomen. Figuur 5 toont hoe vijf van dergelijke inputstroken eruit zouden zien. We zien dat de eerste strook van onze bitmap, bestaande uit alle 1-en, wordt weerspiegeld in de eerste waarde van de ingangen van de nodes. Op deze manier voeren we tijdens de training waarden in de machine in.

Wanneer we de machine voor het eerst initialiseren met willekeurige gewichten en haar vragen een reeks te genereren, creëert zij iets volkomen willekeurigs. Nadat we de machine gedurende 130.000 trainingsperioden hebben getraind, is hij in staat de hele reeks zelf te genereren. Dit betekent dat hij tijdens de training zijn gewichten optimaliseert om niet alleen het samen voorkomen van bits in één tijdstap te leren, maar in een hele reeks.

Magisch, nietwaar? Maar er zit een solide logica achter deze goocheltruc. Laten we het mysterie ontrafelen en kijken waarom deze “Boltzmann Machine met geheugen” werkt.

Dit is de structuur van een Dynamische Boltzmann Machine (DyBM). In een Boltzmann-machine bevat een knooppunt informatie over welke knooppunten het op een bepaald tijdstip activeert. Hierdoor is hij zich bewust van gebeurtenissen die zich samen voordoen, maar heeft hij niet de mogelijkheid om terug te kijken en associaties op te bouwen over verschillende tijdstappen heen. In een DyBM geven de verbindingen tussen de knooppunten echter weer hoe de interactie tussen de knooppunten in de tijd verloopt, en niet alleen in een bepaalde tijdspanne. Het DyBM vergemakkelijkt dit door een geleidingsvertraging tussen de knooppunten toe te voegen.

Met deze nieuwe architectuur heeft een knooppunt informatie over welke andere knooppunten zijn activering in een bepaalde tijdstap T = t hebben gekatalyseerd door hun eigen activiteiten in de afgelopen tijdstappen T = t – 1, T = t – 2, enzovoort. Dit “geheugen” wordt aan een knooppunt toegevoegd in de vorm van een geheugeneenheid. Deze eenheid verandert de waarschijnlijkheid dat een knooppunt op een bepaald moment wordt geactiveerd, afhankelijk van de eerdere waarden van andere knooppunten en de eigen bijbehorende gewichten.

Stellen we ons voor dat we 2 knooppunten A en B hebben. Op een hoog niveau breiden we de notie dat “neuronen die samen vuren, samen bedraden” uit over de tijdsdimensie. Bijvoorbeeld, stel dat de activering van A consequent leidt tot activering van B na twee tijdstappen. Een niet-dynamische Boltzmann machine kan dit patroon niet vastleggen, maar met een DyBM, aangezien de waarde van A met enige vertraging naar B gaat, kan ik het patroon vastleggen dat B = 1 ergens na A = 1. Nu zal de kans dat B = 1 op tijdstap T = t varieren, niet alleen op basis van de waarde van A op T = t, maar ook op basis van de waarden van A op T = t – 1, T = t – 2, enzovoort, afhankelijk van de geleidingsvertraging tussen A en B.

De machine slaat de waarden zo op dat aan recente waarden een groter gewicht wordt toegekend, hetgeen logisch is omdat in het algemeen de meest recente delen van een tijdreeks het meest informatief zijn over de laatste trend. Een DyBM slaat deze informatie op in de geschiktheidsporen. Het Synaptic Eligibility Trace van B bevat de gewogen som van de waarden die B hebben bereikt vanuit A na enige geleidingsvertraging. Het neurale geschiktheidspoor van B bevat de gewogen som van zijn waarden in het verleden.

Gelijk aan standaard recurrente neurale netwerken, kunnen we de DyBM ontvouwen door de tijd heen. De opengevouwen DyBM is een Boltzmann-machine met een oneindig aantal eenheden, die elk de waarde van een knooppunt op een bepaald tijdstip vertegenwoordigen.

Dit is dus de Dynamische Boltzmann-machine: een architectuur die het vermogen heeft de trainingsgegevens niet slechts op één tijdstip opnieuw te genereren, maar in een reeks van die gegevens.

DyBM’s zijn fascinerend, en het volgende deel maakt dat duidelijk.

Deel 4: Confrontatie tussen RNN-Gaussian-DyBM en LSTM

Alle voorbeelden die we tot nu toe hebben gezien, gingen over binaire data (Bernoulli Distributie). Onderzoekers van IBM gingen een stap verder en creëerden een DyBM die Gaussische verdelingen kon modelleren en het voor gebruikers als wij mogelijk maakte om tijdreeksgegevens te modelleren met behulp van DyBM en zijn variaties.

Om de efficiency van een DyBM te controleren, heb ik een aantal tests gedaan waarbij een RNN-Gaussian-DyBM (een DyBM met RNN-laag) werd vergeleken met het huidige state-of-the-art, Long Short-Term Memory Neural Network. De resultaten waren opwindend. Voel je vrij om deze tests zelf uit te voeren, op basis van het script dat hier beschikbaar is.

Laten we eens kijken hoe een DyBM zich verhoudt tot een LSTM in een time-series use case.

Use Case: Voorspel de waarde van het volgende zonnevlekkengetal.

We gebruiken gegevens die het maandelijkse zonnevlekkengetal bevatten dat in een lab in Zürich is berekend van het jaar 1749 tot 1983. De gegevens zijn open source en beschikbaar bij Datamarket – Monthly sunspot number, Zurich, 1749-1983.

Laten we eerst eens kijken hoe de LSTM presteerde.

LSTM

• Architectuur: LSTM Dimensie = 10.
• Prestaties over 10 epochs: Gemiddelde Testscore LSTM = 0.08877 RMSE
• Per epoch tijd om te leren: 8.689403 sec.

Nu zullen we zien hoe een RNN-Gaussian-DyBM het deed op dezelfde gegevens.

Brace yourself, dit wordt een zeer interessante ontdekkingsreis… Klaar?

RNN-Gaussian-DyBM

• Architectuur: RNN Dimensie = 10 en Invoerdimensie = 1
• Prestaties over 10 epochs: Gemiddelde Testscore LSTM = 0.07848 RMSE
• Per epoch tijd om te leren: 0.90547 sec.

Niet alleen loopt het RNN-Gaussian-DyBM in dit geval 10 keer sneller, het levert ook betere prestaties.

Naarmate we het aantal epochs voor de twee modellen opschalen, neemt het tijdsverschil tussen de training van deze twee modellen drastisch toe. De DyBM-responstijd is veel sneller, dus de train – test – deploy-cyclus krimpt en je kunt modellen veel sneller verbeteren.

Maar we hebben het nog niet gehad over het beste deel van DyBM’s: Je kunt ze versnellen met GPU-versnelling. Een DyBM die draait op een GPU op IBM Watson Studio Local met Power AI IBM Cloud Service kan voorspellingen doen voor meer dan 2000 tijdreeksen, elk met een lengte van meer dan 500, in minder dan 10 seconden per epoch. Daarentegen heeft een DyBM die op CPU draait iets meer dan 30 minuten nodig om dezelfde taak uit te voeren. Vergelijk dit resultaat eens met de prestaties van een LSTM op CPU uit het vorige voorbeeld. Stel je de rekenkracht eens voor die dit oplevert. Zie hier voor meer informatie over het versnellen van DyBM’s met GPU’s. Merk op dat je ook LSTM’s kunt versnellen met GPU’s, en dat de prestatievergelijking tussen een versnelde DyBM en een versnelde LSTM zal verschillen.

De volgende keer dat je een tijdreeksprobleem wilt oplossen, probeer Dynamic Boltzmann Machines eens uit. Overweeg om te beginnen met de IBM Research Tokyo GitHub repository voor Dynamic Boltzmann Machines, die je hier kunt vinden.

Zie hieronder voor aanvullend diepgaand onderzoek over Energy-Based Models, Boltzmann Machines en Dynamic Boltzmann Machines:

• A Tutorial on Energy-Based Learning – Yann LeCun, Sumit Chopra, Raia Hadsell, Marc’Aurelio Ranzato, and Fu Jie Huang
• Boltzmann Machines – Geoffrey Hinton
• Boltzmann Machines and Energy-Based Models – Takayuki Osogami (IBM Research – Tokyo)
• Zeven neuronen onthouden sequenties van alfabetische beelden via spike-timing afhankelijke plasticiteit – Takayuki Osogami en Makoto Otsuka
• Nonlineaire Dynamische Boltzmann Machines voor Tijdreeksvoorspelling – Sakyasingha Dasgupta en Takayuki Osogami (IBM Research – Tokio)