Vogliamo che questa macchina generi l’intero set di dati di addestramento da sola o che generi l’intero set di dati di addestramento sulla base di una traccia dai dati originali. Per esempio, data un’immagine bitmap contenente “SCI”, genererebbe “ENCE” da sola dai pesi che ha imparato.
Per avere un’immagine del sistema nella nostra mente, consideriamo la Figura 5.
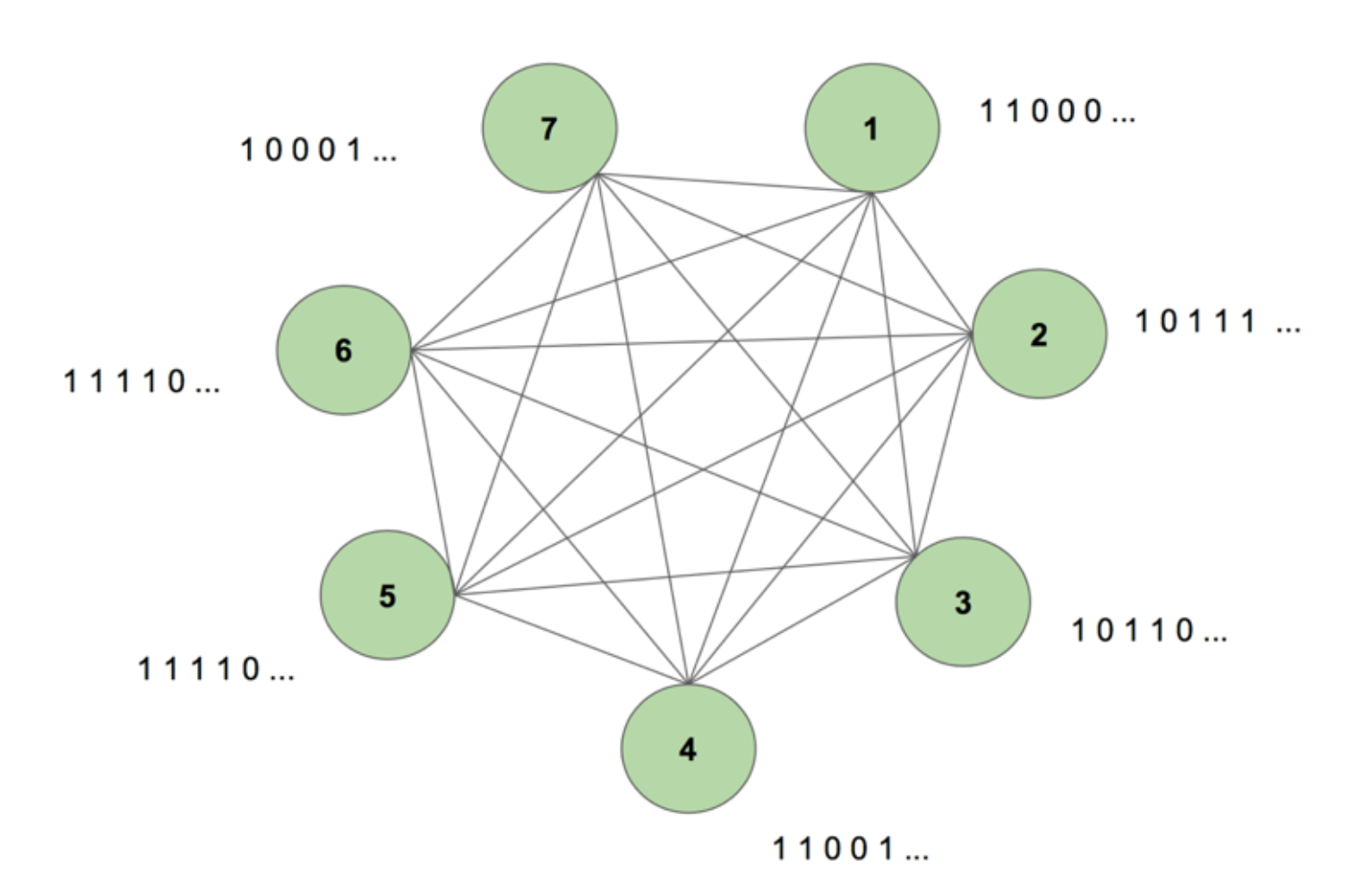
La macchina contiene sette nodi. Un’immagine bitmap 7×35 che rappresenta la parola SCIENZA è la sequenza di destinazione. Un periodo di addestramento consiste nel mostrare alla macchina questa sequenza target una volta. L’obiettivo è suddiviso in 35 strisce di 7 valori e alimentato nella macchina nella stessa sequenza della sua apparizione nell’obiettivo. La figura 5 mostra come sarebbero cinque di queste strisce di input. Vediamo che la prima striscia della nostra bitmap, composta da tutti gli 1, si riflette nel primo valore degli ingressi dei nodi. Questo è il modo in cui inseriamo i valori nella macchina durante l’addestramento.
Quando inizializziamo la macchina con pesi arbitrari e le chiediamo di generare una sequenza, essa crea qualcosa di completamente casuale. Dopo aver addestrato la macchina per 130.000 periodi di allenamento, è in grado di generare l’intera sequenza da sola. Questo significa che durante l’addestramento, ottimizza i suoi pesi per imparare non solo la co-occorrenza dei bit in un tempo, ma in un’intera sequenza.
Magico, vero? Ma c’è una solida logica dietro questo trucco magico. Sveliamo il mistero e vediamo perché questa “macchina di Boltzmann con memoria” funziona.

Questa è la struttura di una macchina di Boltzmann dinamica (DyBM). In una macchina di Boltzmann, un nodo contiene informazioni su quali nodi lo attivano in un certo momento. Questo la rende consapevole degli eventi che si stanno verificando insieme, ma non le dà la capacità di guardare indietro e costruire associazioni attraverso diversi timeteps. Ma in un DyBM le connessioni tra i nodi rappresentano come i nodi interagiscono nel tempo, non solo in un particolare momento. La DyBM facilita questo aggiungendo un ritardo di conduzione tra i nodi.
Con questa nuova architettura, un nodo ha informazioni su quali altri nodi hanno catalizzato la sua attivazione in un certo timestep T = t attraverso le loro attività nei timestep passati T = t – 1, T = t – 2, e così via. Questa “memoria” è aggiunta a un nodo sotto forma di un’unità di memoria. Questa unità modifica la probabilità che un nodo sia attivato in qualsiasi momento, a seconda dei valori precedenti degli altri nodi e dei suoi pesi associati.
Consideriamo di avere 2 nodi A e B. Ad un livello alto, stiamo estendendo la nozione che “i neuroni che sparano insieme, cablano insieme” attraverso la dimensione del tempo. Per esempio, immaginiamo che l’attivazione di A porti coerentemente all’attivazione di B dopo due tempi. Una macchina di Boltzmann non dinamica non cattura questo modello, ma con una DyBM, poiché il valore di A viaggia verso B dopo un certo ritardo, posso catturare il modello che B = 1 qualche volta dopo A = 1. Ora la probabilità che B = 1 al tempo T = t varierà in base non solo al valore di A a T = t, ma anche ai valori di A a T = t – 1, T = t – 2, e così via, a seconda della quantità di ritardo di conduzione tra A e B.
La macchina memorizza i valori in modo che i valori recenti abbiano un peso maggiore, il che ha senso poiché in generale le parti più recenti di una serie temporale sono le più informative sull’ultima tendenza. Una DyBM memorizza queste informazioni nelle tracce di eleggibilità. La traccia di eleggibilità sinaptica di B contiene la somma ponderata dei valori che hanno raggiunto B da A dopo un certo ritardo di conduzione. La traccia di eleggibilità neurale di B contiene la somma ponderata dei suoi valori passati.
Similmente alle reti neurali ricorrenti standard, possiamo spiegare la DyBM attraverso il tempo. La DyBM dispiegata è una macchina di Boltzmann che ha un numero infinito di unità, ognuna delle quali rappresenta il valore di un nodo in un particolare momento.
Quindi, questa è la Dynamic Boltzmann Machine: un’architettura che ha il potere di ricreare i dati di allenamento non solo in un punto nel tempo, ma attraverso una sequenza di quei dati.
Le DyBM sono affascinanti, e la parte che segue porta a casa il punto.
Parte 4: confronto tra RNN-Gaussian-DyBM e LSTM
Tutti gli esempi che abbiamo visto finora hanno avuto a che fare con dati binari (distribuzione Bernoulli). I ricercatori IBM hanno fatto un passo avanti e hanno creato una DyBM che può modellare le distribuzioni gaussiane e ha reso possibile agli utenti come noi di modellare i dati delle serie temporali usando DyBM e le sue varianti.
Per verificare l’efficienza di una DyBM, ho eseguito alcuni test confrontando una RNN-Gaussian-DyBM (una DyBM con strato RNN) e l’attuale stato dell’arte, la rete neurale a memoria lunga e breve termine. I risultati sono stati entusiasmanti. Sentitevi liberi di eseguire questi test per conto vostro, sulla base dello script disponibile qui.
Vediamo come una DyBM si confronta con una LSTM su un caso d’uso di serie temporali.
Caso d’uso: Prevedere il valore del prossimo numero di macchie solari.
Utilizzeremo dati contenenti il Monthly Sunspot Number calcolato in un laboratorio di Zurigo dall’anno 1749 al 1983. I dati sono open source e disponibili da Datamarket – Monthly sunspot number, Zurich, 1749-1983.
Primo, vediamo come si è comportato il LSTM.
LSTM
- Architettura: LSTM Dimensione = 10.
- Performance su 10 epoche: Punteggio medio del test LSTM = 0.08877 RMSE
- Per epoca tempo di apprendimento: 8.689403 sec.

Ora vedremo come una RNN-Gaussiana-DyBM si è comportata sugli stessi dati.
Bracciatevi, questo sarà un viaggio di scoperta molto interessante… Pronti?
RNN-Gaussian-DyBM
- Architettura: RNN Dimensione = 10 e Dimensione di ingresso = 1
- Performance su 10 epoche: Punteggio medio di prova LSTM = 0,07848 RMSE
- Per epoca tempo di apprendimento: 0.90547 sec.

Non solo la RNN-Gaussiana-DyBM è 10 volte più veloce in questo caso, ma offre anche prestazioni migliori.
Come si scala il numero di epoche per i due modelli, la differenza di tempo tra l’addestramento di questi due modelli aumenta drasticamente. Il tempo di risposta dei DyBM è molto più veloce, quindi il ciclo di addestramento – test – distribuzione si riduce ed è possibile migliorare i modelli molto più velocemente.
Ma non abbiamo ancora discusso la parte migliore dei DyBM: È possibile velocizzarli con l’accelerazione della GPU. Un DyBM eseguito su una GPU su IBM Watson Studio Local con Power AI IBM Cloud Service può fare previsioni per oltre 2000 serie temporali, ciascuna di lunghezza superiore a 500, in meno di 10 secondi per epoca. Al contrario, un DyBM in esecuzione su CPU impiegherà poco più di 30 minuti per svolgere lo stesso compito. Confrontate questo risultato con le prestazioni di un LSTM su CPU dell’esempio precedente. Immaginate la potenza di calcolo che questo fornisce. Vedere qui per ulteriori informazioni sull’accelerazione delle DyBM con le GPU. Vale la pena notare che è anche possibile accelerare le LSTM con le GPU, e il confronto delle prestazioni tra una DyBM accelerata e una LSTM accelerata varia.
La prossima volta che volete risolvere un problema di serie temporali, provate le Dynamic Boltzmann Machines. Considerate di iniziare con il repository GitHub di IBM Research Tokyo per le Dynamic Boltzmann Machines, che potete trovare qui.
Vedi sotto per ulteriori ricerche approfondite su modelli basati sull’energia, macchine di Boltzmann e macchine di Boltzmann dinamiche:
- A Tutorial on Energy-Based Learning – Yann LeCun, Sumit Chopra, Raia Hadsell, Marc’Aurelio Ranzato, e Fu Jie Huang
- Macchine di Boltzmann – Geoffrey Hinton
- Macchine di Boltzmann e modelli basati sull’energia – Takayuki Osogami (IBM Research – Tokyo)
- Sette neuroni che memorizzano sequenze di immagini alfabetiche attraverso la plasticità spike-spike- timing dependent plasticity – Takayuki Osogami and Makoto Otsuka
- Nonlinear Dynamic Boltzmann Machines for Time-Series Prediction – Sakyasingha Dasgupta and Takayuki Osogami (IBM Research – Tokyo)