Queremos que esta máquina genere todo el conjunto de datos de entrenamiento por sí misma o que genere todo el conjunto de datos de entrenamiento basándose en una pista de los datos originales. Por ejemplo, dada una imagen de mapa de bits que contenga «SCI», generaría «ENCE» por sí misma a partir de los pesos que ha aprendido.

Para obtener una imagen del sistema en nuestra mente, considere la Figura 5.

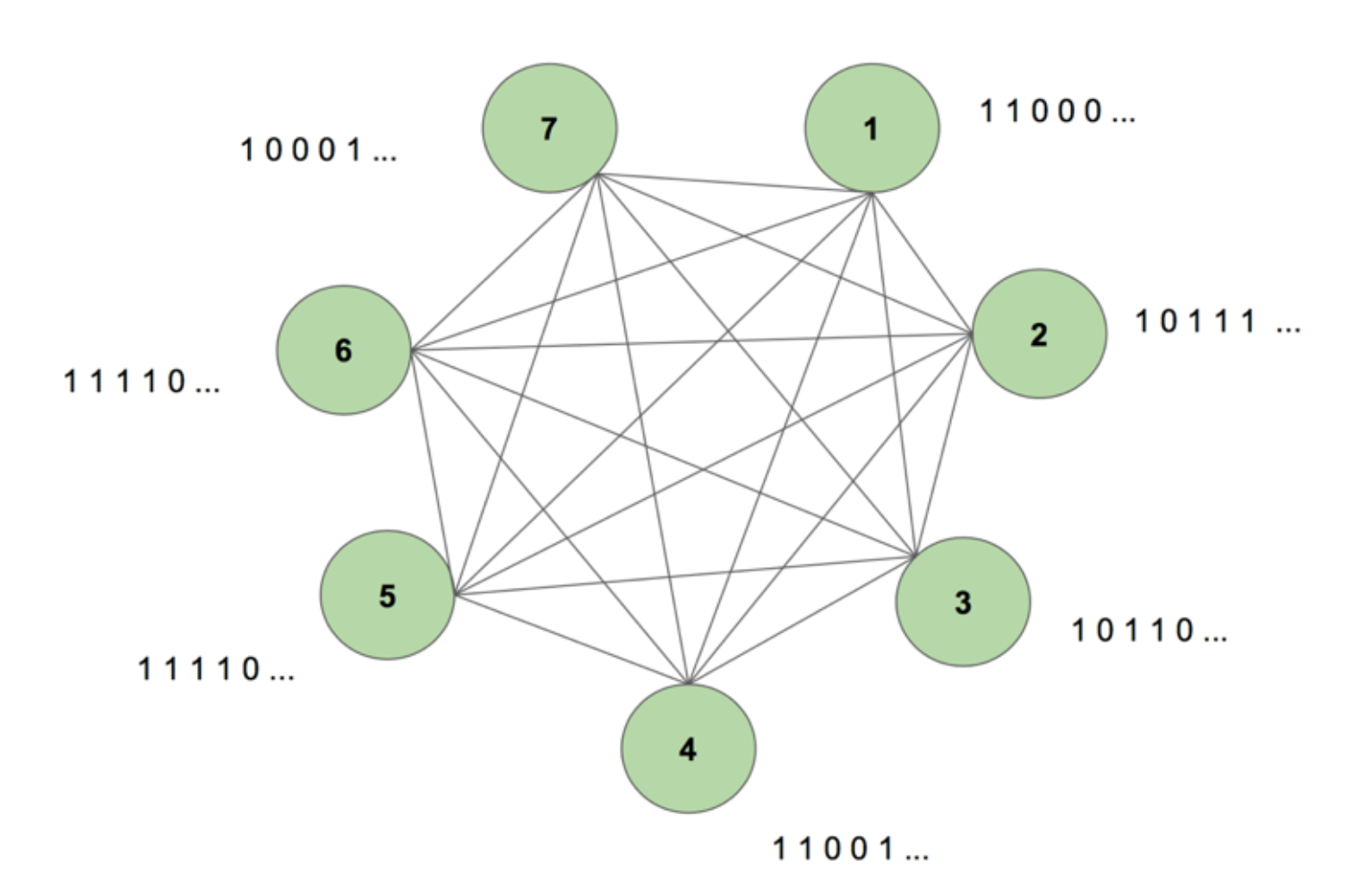
La máquina contiene siete nodos. Una imagen de mapa de bits de 7 por 35 que representa la palabra CIENCIA es la secuencia objetivo. Un periodo de entrenamiento consiste en mostrar a la máquina esta secuencia objetivo una vez. El objetivo se descompone en 35 tiras de 7 valores y se introduce en la máquina en la misma secuencia que su aparición en el objetivo. La figura 5 muestra el aspecto de cinco de estas tiras de entrada. Vemos que la primera tira de nuestro mapa de bits, formada por todos los 1s, se refleja en el primer valor de las entradas de los nodos. Así es como introducimos los valores en la máquina durante el entrenamiento.

Cuando inicializamos por primera vez la máquina con pesos arbitrarios y le pedimos que genere una secuencia, crea algo completamente aleatorio. Después de entrenar la máquina durante 130.000 periodos de entrenamiento, es capaz de generar toda la secuencia por sí misma. Esto significa que durante el entrenamiento, optimiza sus pesos para aprender no sólo la co-ocurrencia de bits en un paso de tiempo, sino a través de toda una secuencia.

Mágico, ¿no? Pero hay una lógica sólida detrás de este truco de magia. Desvelemos el misterio y veamos por qué funciona esta «Máquina de Boltzmann con memoria».

Esta es la estructura de una Máquina Dinámica de Boltzmann (DyBM). En una máquina de Boltzmann, un nodo contiene información sobre los nodos que lo activan en un momento determinado. Esto hace que sea consciente de los eventos que están ocurriendo juntos, pero no le da la capacidad de mirar hacia atrás y construir asociaciones a través de diferentes pasos de tiempo. Sin embargo, en un DyBM las conexiones entre los nodos representan la forma en que éstos interactúan a lo largo del tiempo, no sólo en un paso temporal concreto. El DyBM facilita esto añadiendo un retraso de conducción entre los nodos.

Con esta nueva arquitectura, un nodo tiene información sobre qué otros nodos catalizaron su activación en algún paso de tiempo T = t a través de sus propias actividades en los pasados pasos de tiempo T = t – 1, T = t – 2, y así sucesivamente. Esta «memoria» se añade a un nodo en forma de unidad de memoria. Esta unidad altera la probabilidad de que un nodo se active en cualquier momento, dependiendo de los valores anteriores de otros nodos y de sus propios pesos asociados.

Consideremos que tenemos 2 nodos A y B. En un nivel alto, estamos extendiendo la noción de que «las neuronas que se disparan juntas, se conectan juntas» a través de la dimensión del tiempo. Por ejemplo, imaginemos que la activación de A conduce sistemáticamente a la activación de B después de dos pasos de tiempo. Una máquina de Boltzmann no dinámica no puede capturar este patrón, pero con una DyBM, ya que el valor de A viaja a B después de un cierto retraso, puedo capturar el patrón de que B = 1 en algún momento después de A = 1. Ahora la probabilidad de que B = 1 en el paso de tiempo T = t variará basándose no sólo en el valor de A en T = t, sino también en los valores de A en T = t – 1, T = t – 2, y así sucesivamente, dependiendo de la cantidad de retardo de conducción entre A y B.

La máquina almacena los valores de manera que los valores recientes tienen mayor peso, lo que tiene sentido ya que en general las partes más recientes de una serie de tiempo son las más informativas sobre la última tendencia. Un DyBM almacena esta información en las trazas de elegibilidad. La traza de elegibilidad sináptica de B contiene la suma ponderada de los valores que han llegado a B desde A después de un cierto retraso en la conducción. La traza de elegibilidad neuronal de B contiene la suma ponderada de sus valores pasados.

De forma similar a las redes neuronales recurrentes estándar, podemos desplegar el DyBM a través del tiempo. La DyBM desplegada es una Máquina de Boltzmann que tiene un número infinito de unidades, cada una de las cuales representa el valor de un nodo en un momento determinado.

Así pues, ésta es la Máquina de Boltzmann Dinámica: una arquitectura que tiene el poder de recrear los datos de entrenamiento no sólo en un punto del tiempo, sino a través de una secuencia de esos datos.

Las DyBMs son fascinantes, y la parte que sigue nos lleva al punto de partida.

Parte 4: Enfrentamiento entre RNN-Gaussian-DyBM y LSTM

Todos los ejemplos que hemos visto hasta ahora han tratado con datos binarios (Distribución Bernoulli). Los investigadores de IBM fueron un paso más allá y crearon una DyBM que podía modelar distribuciones gaussianas e hicieron posible que usuarios como nosotros pudiéramos modelar datos de series temporales utilizando DyBM y sus variaciones.

Para comprobar la eficiencia de una DyBM, realicé algunas pruebas comparando una RNN-Gaussian-DyBM (una DyBM con una capa de RNN) y el estado actual de la técnica, la red neuronal de memoria a corto plazo. Los resultados fueron emocionantes. Siéntase libre de ejecutar estas pruebas por su cuenta, sobre la base de la secuencia de comandos disponibles aquí.

Veamos cómo un DyBM se compara con un LSTM en un caso de uso de series de tiempo.

Caso de uso: Predecir el valor del próximo número de manchas solares.

Utilizaremos datos que contengan el número mensual de manchas solares calculado en un laboratorio de Zúrich desde el año 1749 hasta 1983. Los datos son de código abierto y están disponibles en Datamarket – Monthly sunspot number, Zurich, 1749-1983.

Primero, veamos cómo se comportó el LSTM.

LSTM

• Arquitectura: LSTM Dimensión = 10.
• Rendimiento sobre 10 epochs: Puntuación media de la prueba LSTM = 0.08877 RMSE
• Tiempo de aprendizaje por epoch: 8,689403 seg.

Ahora veremos cómo se comportó una RNN-Gaussiana-DyBM con los mismos datos.

Abrázate, este va a ser un viaje de descubrimiento muy interesante… ¿Listo?

RNN-Gaussiana-DyBM

• Arquitectura: RNN Dimensión = 10 y Dimensión de entrada = 1
• Rendimiento en 10 épocas: Puntuación media de la prueba LSTM = 0,07848 RMSE
• Tiempo de aprendizaje por época: 0,90547 seg.

La RNN-Gaussiana-DyBM no sólo se ejecuta 10 veces más rápido en este caso, sino que también ofrece un mejor rendimiento.

A medida que escalamos el número de épocas para los dos modelos, la diferencia de tiempo entre el entrenamiento de estos dos modelos aumenta drásticamente. El tiempo de respuesta de los DyBM es mucho más rápido, por lo que el ciclo de entrenamiento – prueba – despliegue se reduce y puedes mejorar los modelos mucho más rápido.

Pero aún no hemos hablado de la mejor parte de los DyBM: Puedes acelerarlos con la aceleración de la GPU. Un DyBM que se ejecuta en una GPU en IBM Watson Studio Local con Power AI IBM Cloud Service puede hacer predicciones para más de 2000 series temporales, cada una de ellas de más de 500, en menos de 10 segundos por época. En cambio, un DyBM que se ejecute en la CPU tardará algo más de 30 minutos en realizar la misma tarea. Compare este resultado con el rendimiento de un LSTM en la CPU del ejemplo anterior. Imagínate la potencia de cálculo que esto proporciona. Consulta aquí para obtener más información sobre la aceleración de los DyBM con las GPU. Vale la pena señalar que también se pueden acelerar las LSTM con las GPU, y la comparación del rendimiento entre una DyBM acelerada y una LSTM acelerada variará.

La próxima vez que quieras resolver un problema de series temporales, prueba las Máquinas Dinámicas de Boltzmann. Considera comenzar con el repositorio GitHub de IBM Research Tokyo para las Máquinas Dinámicas de Boltzmann, que puedes encontrar aquí.

Vea a continuación la investigación adicional en profundidad sobre los modelos basados en la energía, las máquinas de Boltzmann y las máquinas dinámicas de Boltzmann:

• Un tutorial sobre el aprendizaje basado en la energía – Yann LeCun, Sumit Chopra, Raia Hadsell, Marc’Aurelio Ranzato, y Fu Jie Huang
• Máquinas de Boltzmann – Geoffrey Hinton
• Máquinas de Boltzmann y modelos basados en la energía – Takayuki Osogami (IBM Research – Tokio)
• Siete neuronas que memorizan secuencias de imágenes alfabéticas a través de la plasticidad dependiente de los picos.plasticidad dependiente del tiempo – Takayuki Osogami y Makoto Otsuka
• Máquinas de Boltzmann dinámicas no lineales para la predicción de series temporales – Sakyasingha Dasgupta y Takayuki Osogami (IBM Research – Tokio)