A variancia egy olyan szám, amely azt jelzi, hogy egy számhalmaz milyen messze van egymástól.A variancia megegyezik a négyzetes szórással, tehát “ugyanazt a dolgot” fejezi ki (de erősebben).
Variancia – Példa
Egy vizsgálatban 100 ember 80 próba során egy egyszerű gyorsasági feladatot hajt végre. Minden egyes résztvevő esetében így 80 reakcióidőt (másodpercben) rögzítenek. Ezen adatok egy része az alábbiakban látható.

Az ehhez hasonló vizsgálatokban jellemzően azt látjuk, hogy az emberek egyre gyorsabbak lesznek, minél gyakrabban hajtják végre a sebességfeladatot. Vagyis az átlagos reakcióidő a próbák során általában csökken.
Az egyes emberek között is jellemzően kisebb lesz a reakcióidő eltérése, amennyiben gyakrabban hajtják végre a feladatot. Technikailag azt mondjuk, hogy a variancia csökken a próbák során. Az alábbi táblázat ezt szemlélteti az 1.,4.,7. és 10. próbákra vonatkozóan.
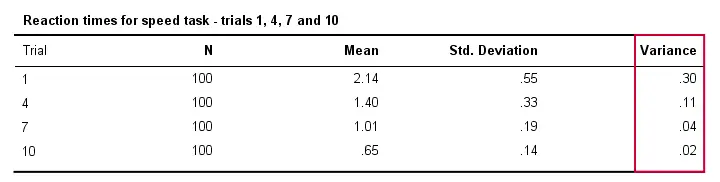
Variancia és hisztogram
Az előző táblázatunk adatainak szemléltetésére kiválóan alkalmas az egyes próbákra vonatkozó hisztogram. Az alábbi ábra így szemlélteti, hogy a résztvevők a próbák során egyre gyorsabbak lettek; az 1. próbától a 10. próba felé haladva a hisztogram sávjai balra, a 0 másodperc felé mozognak.
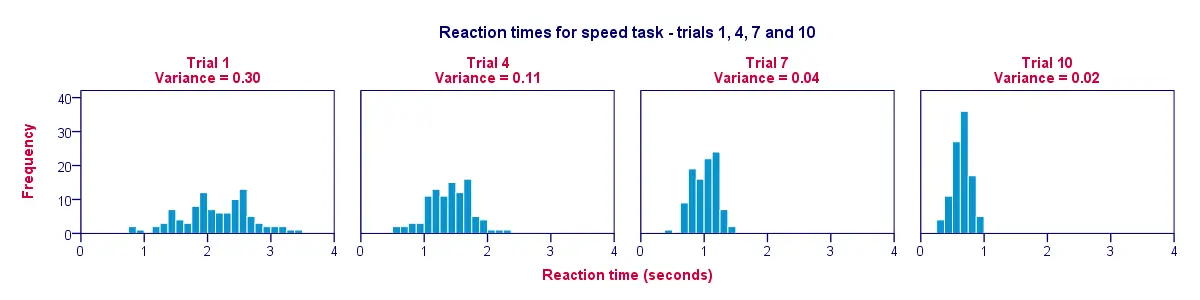
A másik megállapítás, hogy a hisztogramok keskenyebbek (és ezért magasabbak) lesznek, ahogy az 1. próbától a 10. próba felé haladunk; ez azt mutatja, hogy a kísérlet előrehaladtával egyre kevésbé változik a reakcióidő a résztvevőink között. A variancia csökken a próbák során.
Variancia – populációs képlet
A variancia kiszámításának alapvető képlete a következő
$$S^2 = \frac{\sum(X – \overline{X})^2}{n}$$
Azt javasoljuk, hogy próbálja megérteni, mit jelent ez a képlet, mert ez sokat segít az ANOVA (= varianciaanalízis) megértésében. Ezért egy maréknyi adaton fogjuk bemutatni.
Variancia – GoogleSheets
Az egyszerűség kedvéért az adatainkat az első 5 résztvevő első kísérletére szűkítjük le. Ez az 5 reakcióidő -és a varianciájuk manuális kiszámítása- ebben a GoogleSheetben található.
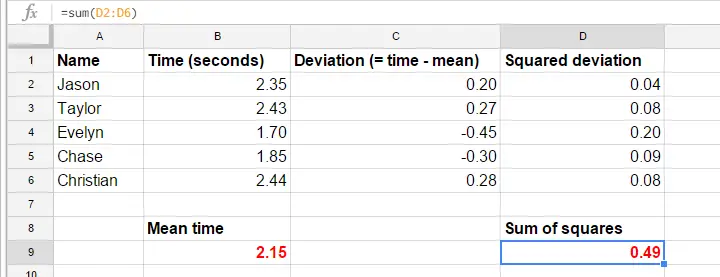
Variancia – Számítási lépések
A GoogleSheetben található képletek pontosan megmutatják, hogyan kell kiszámítani a varianciát. Az alapvető lépések a következők:
- számítsuk ki az átlagos reakcióidőt (2,15);
- számítsuk ki az eltérési pontszámokat (reakcióidő mínusz átlagos reakcióidő);
- számítsuk ki a négyzetes eltérési pontszámokat;
- adjuk össze a négyzetes eltérési pontszámokat. Az eredmény (0,49) a négyzetek összege, az ANOVA fő építőeleme;
- osszuk el a négyzetek összegét a megfigyelések számával (5 reakcióidő).
Alternatívaként kiszámíthatjuk a varianciát, ha valamelyik cellába beírjuk a =VARP(B2:B6) értéket (a B2:B6 cellák tartalmazzák az 5 reakcióidőnket). A VARP a “varianciapopuláció” rövidítése. Az OpenOffice és az MS Excel is tartalmaz hasonló képleteket.
Variancia – minta képlet
A szóráshoz hasonlóan, ha adataink egy egyszerű véletlen minta egy sokkal nagyobb populációból, a fent említett képlet szisztematikusan alábecsüli a populáció varianciáját. Ebben az esetben egy kissé más képletet fogunk használni:
$$S^2 = \frac{\sum(X_i – \overline{X})^2}{n – 1}$$
Az, hogy melyik képletet használjuk, tehát az adatainktól függ: tartalmazzák-e a teljes populációt, amelyet vizsgálni szeretnénk, vagy csak egy egyszerű minta ebből a populációból?
Mivel a 100 résztvevőnk egyértelműen egy minta, a minta képletét fogjuk használni. A GoogleSheetsben a =VAR(B2:B6) beírása valamelyik cellába a minta varianciáját adja vissza.
Variancia az SPSS-ben
Mennyire tudjuk, a populációs variancia képlete teljesen hiányzik az SPSS-ből, és ezt súlyos hibának tartjuk. Ehelyett az SPSS mindig a minta képletét használja. ez vonatkozik mind az alanyok közötti varianciára (amelyet ebben a bemutatóban tárgyalunk), mind az alanyokon belüli varianciára. A vonatkozó kimenet az alábbiakban látható:

Ezzel a kimeneti táblázattal kapcsolatban azt is vegye figyelembe, hogy a variancia valóban a standard eltérés négyzete (a kerekítéstől eltekintve).
A varianciával kapcsolatban ennyi. Reméljük, hogy ez a bemutató hasznosnak bizonyult annak megértésében, hogy mi is az a variancia.