A nemkívánatos konvolúció az analóg információátvitel velejáró problémája. Például a következők mindegyike modellezhető konvolúcióként: a kép elmosódása egy remegő kamerában, visszhangok a távolsági telefonhívásokban, az analóg érzékelők és elektronika véges sávszélessége stb. A dekonvolúció a jel szűrésének folyamata a nemkívánatos konvolúció kompenzálására. A dekonvolúció célja, hogy a jelet úgy állítsa vissza, ahogy az a konvolúció előtt volt. Ehhez általában ismertnek kell lennie a konvolúció jellemzőinek (azaz az impulzus- vagy frekvenciaválasznak). Ez megkülönböztethető a vak dekonvolúciótól, ahol a parazita konvolúció jellemzői nem ismertek. A vak dekonvolúció sokkal nehezebb probléma, amelynek nincs általános megoldása, és a megközelítést az adott alkalmazáshoz kell igazítani.

A dekonvolúciót az időtartományban szinte lehetetlen megérteni, de a frekvenciatartományban eléggé egyszerű. Az eredeti jelet alkotó minden egyes szinuszoid amplitúdóját és/vagy fázisát meg lehet változtatni, miközben áthalad a nemkívánatos konvolúción. Az eredeti jel kinyeréséhez a dekonvolúciós szűrőnek vissza kell vonnia ezeket az amplitúdó- és fázisváltozásokat. Például

ha a konvolúció egy szinuszoid amplitúdóját 0,5-el változtatja meg 30 fokos fáziseltolódással, akkor a dekonvolúciós szűrőnek a szinuszoidot 2,0-val kell felerősítenie -30 fokos fáziseltolódással.

A dekonvolúció bemutatására egy gammasugár-detektor példáját fogjuk használni. Amint a 17-3. ábrán látható, ez a készülék két részből, egy szcintillátorbólés egy fénydetektorból áll. A szcintillátor egy speciális típusú átlátszó anyag, például nátrium-jodid vagy bizmut-germanát. Ezek a vegyületek az egyes gammasugarakban lévő energiát rövid ideig látható fénysugárzássá változtatják. Ezt a fényt

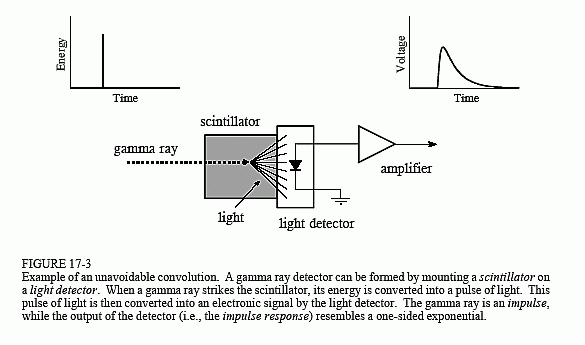
egy fényérzékelő, például egy fotodióda vagy fotomultiplier cső elektronikus jellé alakítja át. A detektor által előállított minden egyes impulzus egy egyoldalú exponenciálishoz hasonlít, a sarkok némi lekerekítésével. Ezt az alakot a használt szcintillátor jellemzői határozzák meg. Amikor az agamma-sugárzás energiáját a szcintillátorba juttatja, a közeli atomok magasabb energiaszintre gerjesztődnek. Ezek az atomok véletlenszerűen deexcitálnak, és egy-egy látható fényfoton keletkezik. A végeredmény egy fényimpulzus, amelynek amplitúdója néhány száz nanoszekundum alatt csökken (nátrium-jodid esetében). Mivel minden egyes gammasugár érkezése impulzus, a detektor kimeneti impulzusa (azaz az egyoldalas exponenciális) a rendszer impulzusválasza.

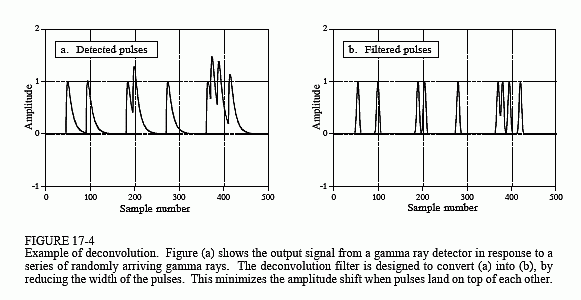
A 17-4a. ábra a detektor által a véletlenszerűen érkező gammasugarakra adott válaszként létrehozott impulzusokat mutatja. Az információ, amit ebből a kimenő jelből szeretnénk kinyerni, az az egyes impulzusok amplitúdója, amely arányos az őket létrehozó gammasugár energiájával. Ez hasznos információ, mert az energia érdekes dolgokat árulhat el arról, hogy a gammasugár hol járt. Például orvosi információkat szolgáltathat egy betegről, megmondhatja egy távoli galaxis korát, felderíthet egy bombát a repülőgépek poggyászában stb.

Minden rendben lenne, ha csak alkalmanként észlelnének gammasugárzást, de ez általában nem így van. Ahogy az (a) ábrán látható, két vagy több impulzus átfedheti egymást,eltolva a mért amplitúdót. Az egyik megoldás erre a problémára a detektor kimeneti jelének dekonvolválása, ami keskenyebbé teszi az impulzusokat, így kevesebb halmozódás következik be. Ideális esetben azt szeretnénk, ha minden egyes impulzus hasonlítana az eredeti impulzushoz. Amint azt gyaníthatjuk, ez nem lehetséges, és meg kell elégednünk egy véges hosszúságú, de a detektált impulzusnál lényegesen rövidebb impulzussal. Ezt a célt szemlélteti a 17-4b. ábra.

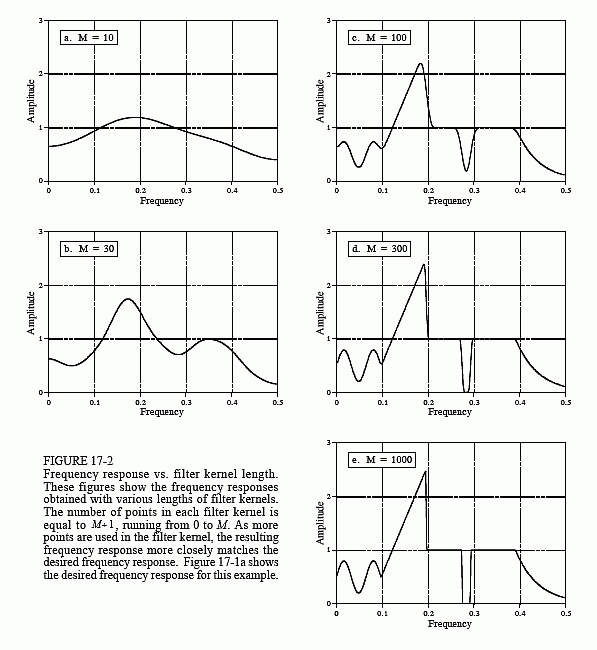
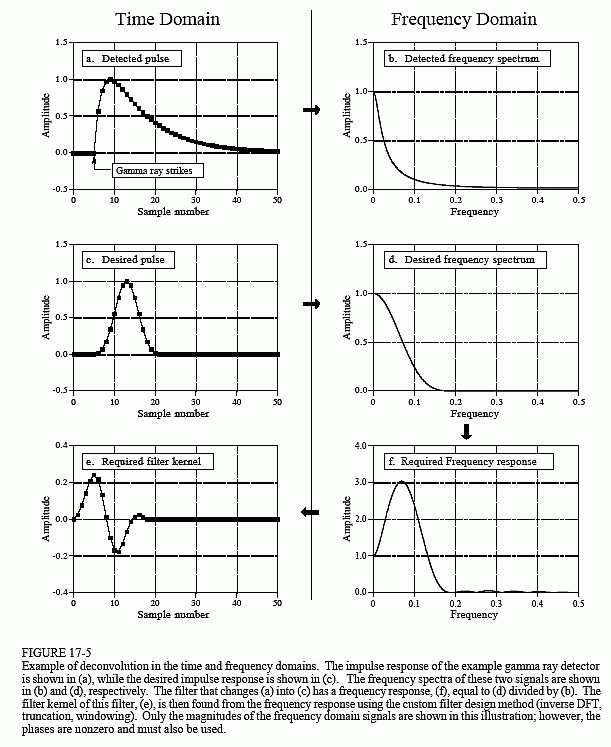
Még ha a detektorjel információi az időtartományban vannak kódolva,elemzésünk nagy részét a frekvenciatartományban kell elvégeznünk, ahol a probléma könnyebben érthető. A 17-5a. ábra a detektor által előállított jelet mutatja(amit ismerünk). A c) ábra az a jel, amelyet szeretnénk, hogy legyen (szintén valami, amit tudunk). Ezt a kívánt impulzust önkényesen úgy választottuk ki, hogy ugyanolyan alakú legyen, mint egy Blackman-ablak, amelynek hossza körülbelül egyharmada az eredeti impulzus hosszának. A célunk az, hogy megtaláljuk azt a szűrőmagot (e), amely az (a) jelével konvolválva a (c) jelet eredményezi. Egyenlet formájában: ha a * e = c, és adott a és c, találjuk meg.

Ha ezeket a jeleket összeadással vagy szorzással kombinálnánk a konvolúció helyett, a megoldás egyszerű lenne: a kivonással “de-addáljuk”, az osztással pedig “de-multiplikáljuk”. A konvolúció más; nincs egyszerűinverz művelet, amelyet “dekonvolúciónak” nevezhetünk. A konvolúció túl rendetlen ahhoz, hogy az időtartománybeli jelek közvetlen manipulálásával vissza lehessen csinálni.

Szerencsére ez a probléma egyszerűbb a frekvenciatartományban. Ne feledjük,a konvolúció az egyik tartományban megfelel a szorzásnak a másik tartományban. Ismét a 17-5. ábrán látható jelekre utalva: ha b × f = d, és adott b és d, találjuk meg f-et. Ezt a problémát könnyű megoldani: a szűrő frekvenciaválasza (f) a kívánt impulzus (d) frekvenciaspektruma osztva a detektált impulzus (b) frekvenciaspektrumával. Mivel az érzékelt impulzus aszimmetrikus, nem nulla fázisú lesz. Ez azt jelenti, hogy komplex osztást kell alkalmazni (azaz egy & nagyságú fázist kell osztani egy másik & nagyságú fázissal). Ha elfelejtette volna, a 9. fejezet meghatározza, hogyan kell elvégezni egy spektrum komplex osztását egy másikkal. A szükséges szűrőmagot, (e), ezután az egyéni szűrőmódszerrel (IDFT, shift, truncate, &multiply by a window) találjuk meg a frekvenciaválaszból.

A dekonvolúció által elérhető javulásnak vannak határai. Más szóval, ha mohó leszel, a dolgok szétesnek. A mohóvá válás ebben a példában azt jelenti, hogy megpróbáljuk a kívánt impulzust túlságosan szűkre szabni. Nézzük meg, mi történik. Ha a kívánt impulzust keskenyebbé tesszük, a frekvencia spektrumának több magas frekvenciájú komponenst kell tartalmaznia. Mivel ezek a nagyfrekvenciás komponensek nagyon alacsony amplitúdójúak az érzékelt impulzusban, a szűrőnek nagyon nagy erősítéssel kell rendelkeznie ezeken a frekvenciákon. Például az (f) mutatja, hogy néhány frekvenciát háromszorosára kell szorozni ahhoz, hogy a kívánt impulzust elérjük (c) pontban. Ha a kívánt impulzust keskenyebbé tesszük, a dekonvolúciós szűrő erősítése még nagyobb lesz a magas frekvenciákon.

A probléma az, hogy a kis hibák ebben a helyzetben nagyon megbocsáthatatlanok. Például,ha valamilyen frekvenciát 30-zal erősítenek, amikor csak 28-ra van szükség, a dekonvolváltjel valószínűleg egy káosz lesz. Amikor a dekonvolúciót nagyobb teljesítményszintre tolják, a nem kívánt konvolúció jellemzőit nagyobb pontossággal és precizitással kell megérteni. A valós alkalmazásokban mindig vannak ismeretlenek, amelyeket olyan gonosztevők okoznak, mint: elektronikus zaj, hőmérsékleti drift, az eszközök közötti eltérések stb. Ezek az ismeretlenek korlátot szabnak annak, hogy a dekonvolúció milyen jól fog működni.

Még ha a nem kívánt konvolúciót tökéletesen megértjük, akkor is van egy tény, amely korlátozza a dekonvolúció teljesítményét: a zaj. Például a legtöbb nemkívánatos konvolúció aluláteresztő szűrő formájában valósul meg, csökkentve a jel magas frekvenciájú összetevőinek amplitúdóját. A dekonvolúció ezt úgy korrigálja, hogy felerősíti ezeket a frekvenciákat. Ha azonban ezeknek a komponenseknek az amplitúdója a rendszer saját zaja alá esik, az ezekben a frekvenciákban rejlő információ elvész. Ezt semmilyen jelfeldolgozással nem lehet visszanyerni. Örökre elveszett. Adios! Viszlát! Sayonara! Ha megpróbáljuk visszaszerezni ezt az adatot, az csak felerősíti a zajt. Szélsőséges esetben egyes frekvenciák amplitúdója teljesen nullára csökkenhet. Ez nem csak eltörli az információt, hanem megpróbálja elérni, hogy a dekonvolúciós szűrő végtelen erősítést kapjon ezeken a frekvenciákon. A megoldás: tervezzen kevésbé agresszív dekonvolúciós szűrőt és/vagy szabjon korlátokat arra, hogy mekkora erősítés megengedett bármelyik frekvencián.

Milyen messzire lehet elmenni? Mennyire mohó a túl mohó? Ez teljesen attól függ, hogy milyen problémát támadsz. Ha a jel jól viselkedik és alacsony a zajszintje, akkor valószínűleg jelentős javulás érhető el (gondoljunk az 5-10-szeresére). Ha a jel idővel változik, nem különösebben jól érthető vagy zajos, akkor közel sem lesz ilyen jó (gondoljunk 1-2 faktorosra). A sikeres dekonvolúcióhoz rengeteg tesztelésre van szükség. Ha valamilyen szinten működik, próbáljon tovább menni; tudni fogja, ha szétesik. Semmilyen mennyiségű elméleti munka nem teszi lehetővé, hogy megkerülje ezt aziteratív folyamatot.

A dekonvolúció frekvenciatartományban kódolt jelekre is alkalmazható. Klasszikus példa erre a híres operaénekes, Enrico Caruso (1873-1921) régi felvételeinek helyreállítása. Ezek a felvételek modern mércével mérve nagyon kezdetleges berendezésekkel készültek. A legjelentősebb problémát a hangfelvételhez használt hosszú csöves felvevőkürt rezonanciái jelentik. Amikor az énekes véletlenül elér egy ilyen rezonanciafrekvenciát, a felvétel hangereje hirtelen megnő. A digitális dekonvolúció javította e felvételek szubjektív minőségét azáltal, hogy

csökkentette a hangos foltokat a zenében. Mi csak az általános módszert ismertetjük;a részletes leírásért lásd az eredeti cikket: T. Stockham, T. Cannon, andR. Ingebretsen, “Blind Deconvolution Through Digital Signal Processing”,Proc. IEEE, vol. 63, Apr. 1975, pp. 678-692.

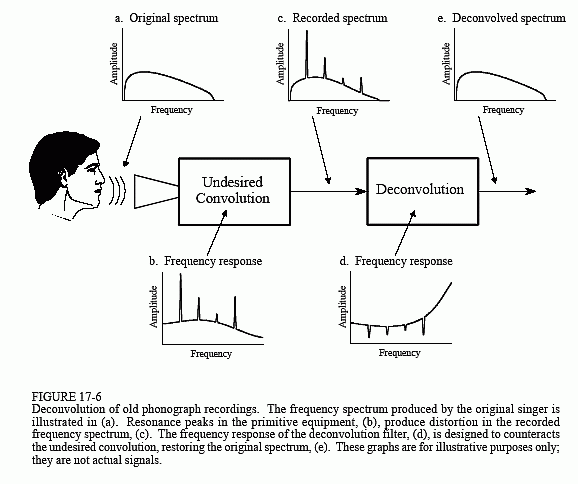
A 17-6. ábra mutatja az általános megközelítést. Az eredeti hangjel frekvenciaspektrumát az a) pont szemlélteti. A (b) ábra a hangrögzítő berendezés frekvenciaválaszát mutatja, egy viszonylag sima görbét, leszámítva néhány éles rezonanciacsúcsot. A rögzített jel spektruma, amelyet a(c) ábrázol, megegyezik az (a) valódi spektrummal, megszorozva a (b) egyenetlen frekvenciaválasz-szal. A dekonvolúció célja a nemkívánatos konvolúció ellensúlyozása. Más szóval, a dekonvolúciós szűrő frekvenciaválaszának,(d), a (b) fordítottjának kell lennie. Ez azt jelenti, hogy a (b) minden csúcsát a (d) megfelelő mélyedésével kell megszüntetni. Ha ez a szűrő tökéletesen lenne kialakítva, akkor a kapott jel spektruma, (e), megegyezne az eredetivel.

Itt a bökkenő: az eredeti felvevőkészüléket már régen kidobták, és a frekvenciaválasza, (b), rejtély. Más szóval, ez egy vakdekonvolúciós probléma; ha csak (c) van, hogyan tudjuk meghatározni (d)?

A vak dekonvolúciós problémákat általában úgy támadják meg, hogy becslést vagy feltételezést tesznek az ismeretlen paraméterekre vonatkozóan. Ennek a példának a kezeléséhez feltételezzük, hogy az eredeti zene átlagspektruma megegyezik ugyanannak a zenének az átlagspektrumával, amelyet egy mai énekes ad elő modern berendezéssel. Az átlagos spektrumot a 9. fejezetben leírt technikákkal találjuk meg: a jelet nagyszámú szegmensre bontjuk, minden egyes szegmens DFT-jét vesszük, poláris formára alakítjuk, majd a nagyságokat együttesen átlagoljuk. A legegyszerűbb esetben az ismeretlen frekvenciaválasz a régi felvétel átlagos spektrumának és a modern felvétel átlagos spektrumának hányadosa. (A Stockham et al. által használt módszer egy kifinomultabb technikán, az úgynevezett homomorfikus feldolgozáson alapul, amely jobb becslést ad a felvételi rendszer jellemzőiről).