Amint a fény visszaverődik vagy átereszt egy anyagi szerkezetről, a polarizáció megváltozik. Az ellipszometria ezt a választ méri, amely az egyes anyagok optikai tulajdonságaitól és vastagságától függ. Az ellipszometriát elsősorban az optikai állandók és a filmvastagság meghatározására használják, de az összetétel, a kristályosság, az érdesség, az adalékkoncentráció és más, az optikai válasz változásával összefüggő anyagi tulajdonságok jellemzésére is.
Az alkalmazási területek a fizikai tudományok alapkutatása, a félvezető- és adattárolási megoldások, a síkképernyők, a kommunikáció, a bioérzékelők és az optikai bevonatipar. Az ellipszometria emellett rugalmasan alkalmazható a legtöbb anyagtípus mérésére: dielektrikumok, félvezetők, fémek, szupravezetők, szerves anyagok, biológiai bevonatok és kompozitok.
Polarizált fény meghatározása
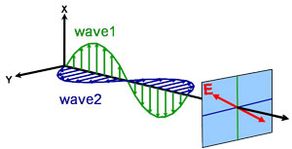
A fényt a térben terjedő elektromágneses hullámként írhatjuk le. Azt, ahogyan egy elektromágneses hullám mezeje a tér és az idő függvényében viselkedik, polarizációnak nevezzük. A fény akkor tekinthető polarálatlannak, ha irányultsága és fázisa teljesen tetszőleges. Az ellipszometria azonban polarizált fényt mér – olyan elektromos mezőt, amely egy meghatározott útvonalat követ, és bármely adott ponton határozott alakkal rendelkezik. A z irányban terjedő elektromágneses hullámot az x- és y-komponensével lehet leírni, mivel az elektromos mezője mindig merőleges a terjedési irányra. Ha két ortogonális fényhullám fázisban van, a keletkező fény lineárisan polarizált. Az orientációját a relatív amplitúdók határozzák meg. A fény akkor tekinthető cirkulárisan polarizáltnak, ha az ortogonális hullámok 90°-kal fázison kívül vannak, és azonos amplitúdóval rendelkeznek. A leggyakoribb polarizáció elliptikus, amely tetszőleges amplitúdójú és fázisú ortogonális hullámokat kombinál. Innen kapta a nevét az ellipszometria.
A polarizáció különböző típusai:
Lineáris
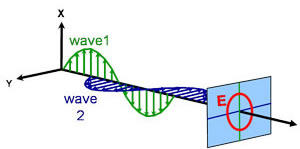
Cirkuláris
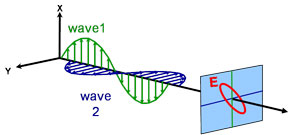
Elliptikus
Optikai tulajdonságok
A fény anyaggal való kölcsönhatását meghatározó optikai tulajdonságokat két értékkel írjuk le. Ezeket általában komplex számként ábrázolják. A komplex törésmutató (ñ) az indexből (n) és egy kioltási együtthatóból (k) áll:
![]()
Az optikai tulajdonságok komplex dielektromos függvényként is ábrázolhatók:
![]()
a konvenciók közötti következő összefüggéssel:
![]()
A mutató az anyagban haladó fény fázissebességét ábrázolja a vákuumban haladó fény sebességéhez, c:
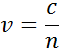
A magasabb indexű anyagba belépve a fény lelassul. Mivel a fényhullámok frekvenciája nem változik, a hullámhossz lerövidül. A hullámok energiaveszteségét az anyagban az extinkciós együtthatóval írjuk le, amely az abszorpciós együtthatóval a következőképpen függ össze:
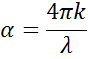
A Beer-törvény szerint a fény elnyelő anyagban veszít intenzitásából. Az extinkciós együttható mutatja, hogy milyen gyorsan tűnik el a fény egy anyagban.
![]()
A 4. ábra egy fényhullámot mutat, amely két különböző tulajdonságú anyagon halad át, mielőtt visszatér a környezetbe.
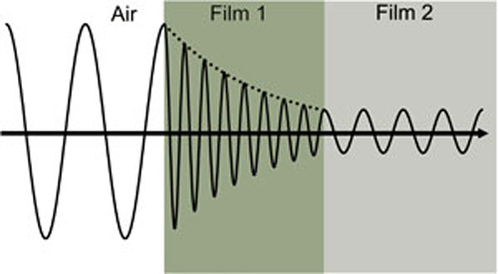
4. ábra: A fényhullám a levegőből az elnyelő Film 1, majd az átlátszó Film 2 anyagba halad. A fázissebesség és a hullámhossz mindkét anyagban változik a törésmutató függvényében (Film 1: n=4, Film 2: n=2).
A hullámhossz határozza meg az optikai állandókat. Az 5. ábra a TiO2 optikai állandókat mutatja az UV-tól az IR-ig. A különböző folyamatok miatt, amelyek energiát vonnak el a fényhullámból, az abszorpció (k>0) mind az UV, mind az IR tartományban bekövetkezik. Az IR-abszorpciót általában molekula- vagy fononrezgés vagy szabad hordozók okozzák. Az UV-abszorpció általában elektronátmenetek miatt következik be, ahol a fényenergia elektronokat gerjeszt magasabb állapotokba. Az 5. ábra mutatja, hogy a feltételezett vagy valós optikai állandók nem függetlenek, hanem matematikailag összekapcsolódnak a Kramers-Kronig-összefüggéseken keresztül.
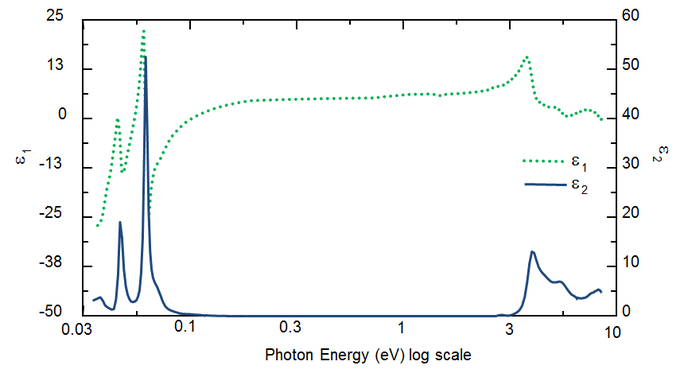
5. ábra: Komplex dielektromos függvény TiO2 filmre az IR (kis eV) és az UV (nagy eV) hullámhosszok között.
Fény és anyagok kölcsönhatása
Amikor a fény kölcsönhatásba lép egy anyaggal, ez határfeltételekhez vezet a határfelületen. Ennek során a Maxwell-egyenleteknek mindig teljesülniük kell. Az alábbi ábra azt mutatja, hogy a beeső fény hogyan verődik vissza és hogyan törik meg a határfelületen. A beeső sugár és a minta normálisa közötti szög (θi) megegyezik a visszavert szöggel (θr). Az anyagba belépő fény θt szögben törik meg, amelyet a következő szög ad:
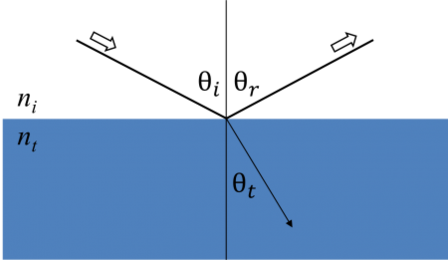
6. ábra: A fény visszaverődik és megtörik a Snell-törvény szerint.
Minden határfelületen a fény egy része visszaverődik, míg a többi a megtörési szögben átereszt. A peremfeltételektől függően különböző megoldások érvényesek a minta felületével párhuzamos és arra merőleges elektromos mezőkre. A fény így a beesési síkhoz képest ortogonális komponensekre osztható (p- és s-polarizált). Mindkét komponens külön-külön számítható. Fresnel így írta le az anyagok közötti határfelületen visszavert és áteresztett fény mennyiségét:
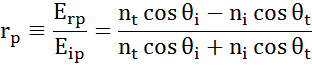
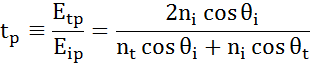
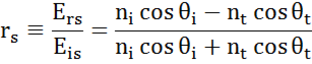
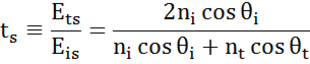
Vékonyfilmes és többrétegű szerkezeteknél több határfelület fordul elő megfelelő Fresnel-féle reflexiós és transzmissziós együtthatóval. A visszavert vagy áteresztett sugár helyes meghatározásához az egyes fénykomponensek relatív fázisát kell követni. A film fázisvastagságát így a következőképpen határozzuk meg:
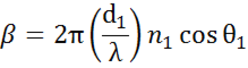
Mikor több fényhullám egymásra helyeződik, interferencia lép fel, amely az egyes fényhullámok relatív fázisától függ. Az alábbi ábra a visszavert fényhullámok kombinációját és a hozzájuk tartozó Fresnel-számításokat mutatja.
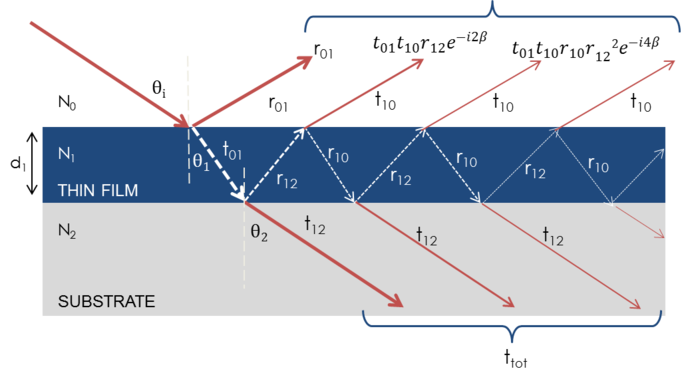
7. ábra: A fény minden egyes határfelületen visszaverődik és megtörik, ami egy vékony filmben több sugárnyalábot eredményez. A sugárinterferencia az elektromos mezők relatív fázisától és amplitúdójától függ. A sugárreakciót a Fresnel-féle reflexiós és transzmissziós együtthatókkal lehet kiszámítani.
Mérések
Az ellipszometria elsősorban azt méri, hogy a p- és s-komponensek hogyan reagálnak egymáshoz képest a reflexió vagy transzmisszió során. Tehát egy referenciasugár mindig része a kísérletnek. Egy ismert polarizációt reflektálnak vagy sugároznak a mintáról, és a kimeneti polarizációt mérik. A polarizáció változása az ellipszometriás mérés:
![]()
A 6. ábrán egy tipikus minta ellipszometriás mérése látható. A lineárisan beeső fénynek p- és s-komponensei is vannak. A visszavert fény amplitúdó- és fázisváltozást mutat mind a p-, mind az s-polarizált fény esetében. Ezeket a változásokat ellipszometriával mérjük.

Az ellipszometriai adatok gyűjtéséhez a következőkre van szükség: fényforrás, polarizációs generátor, minta, polarizációs analizátor és detektor. Mind a polarizációs generátor, mind az analizátor olyan optikai alkatrészekből áll, amelyek a polarizációt manipulálják: kompenzátorok, polarizátorok és fázismodulátorok. A tipikus ellipszométer-konfigurációk forgó analizátort (RAE), forgó polarizátort (RPE), forgó kompenzátort (RCE) és fázismodulátort (PME) tartalmaznak. Az alábbi ábra egy RAE konfigurációt mutat.
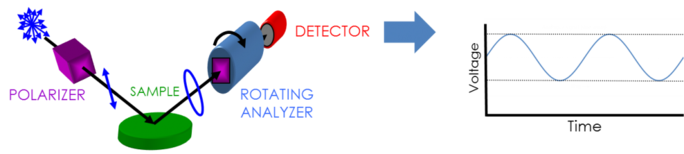
A polarizálatlan fényt egy fényforrás állítja elő, majd átküldi egy polarizátoron. A polarizátor úgy van beállítva, hogy csak egy bizonyos elektromos mezőorientációjú fényt engedjen át. Mivel a polarizátor tengelye a p- és s-s síkok közé van igazítva, mindkettő eléri a minta felületét. Az immár lineárisan polarizált fény visszaverődik a minta felületéről, így elliptikusan polarizált lesz, majd egy folyamatosan forgó polarizátoron (az “analizátoron”) keresztül küldik. Az áthaladó fény mennyisége a polarizátornak a minta elektromos mezejének ellipsziséhez viszonyított orientációjától függ. A visszavert polarizáció meghatározásához a fényt a detektorban elektronikus jellé alakítják át. Ennek az adatnak a megállapított bemeneti polarizációval való összehasonlítása információt szolgáltat a minta visszaverődése által okozott változásról: a Psi és a Delta ellipszometriai mérése.
Adatelemzés
Az ellipszometriát a fény polarizációjában bekövetkező változások mérésével az anyagfilm vastagságának vagy az optikai állandók meghatározására használják. Az ellipszometriás mérésből “pszeudo” optikai állandók származtathatók az egyetlen visszaverődésre meghatározott adatok megfordításával. Ez hasznos ömlesztett anyag esetén.
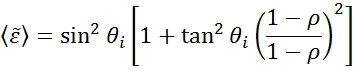
A fenti egyenlet nem számol semmilyen felületi réteggel. Mindazonáltal az ömlesztett anyagokban általában van felületi oxid vagy érdesség. A közvetlen inverzió ezeket az adatokat az ömlesztett optikai állandók részeként tartalmazza. Az ellipszometriai méréseknél alkalmazott tipikus adatelemzési folyamat áttekintését lásd a 10. ábrán. Mivel pontos egyenlet nem írható fel, regresszióelemzésre van szükség. A válasz gyakran túlhatározott, mindössze néhány ismeretlen és több száz kísérleti adatpont esetén. A regresszióelemzés lehetővé teszi, hogy az összes mért adatot bevonjuk a megoldás meghatározásába.
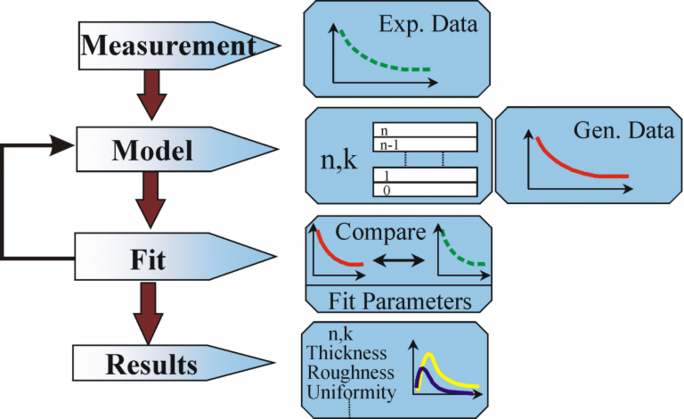
10. ábra: Folyamatdiagram az ellipszometriás adatelemzéshez.
Az adatelemzéshez a következő eljárást alkalmazzuk: a mintát megmérjük, és a mintáról modellt készítünk. E modell segítségével kiszámítják a Fresnel-egyenletekből feltételezett eredményeket, amelyek leírják az egyes anyagok vastagságát és optikai állandóit. Ha ezek az értékek ismeretlenek, akkor az előzetes számítás értékelésére kerül sor. A számított értékeket összehasonlítjuk a kísérleti adatokkal. A kísérleti és a számítási adatok jobb egyezése érdekében az ismeretlen anyagadatok változtathatók. A kísérleti adatpontoknak azonban mindig többnek kell lenniük, mint az ismeretlen paramétereknek. Például egy egyhullámú ellipszométerrel legfeljebb két anyagtulajdonság határozható meg, mivel az pontosan két adatpontot eredményez: Ψ, Δ (Psi és Delta). A regressziót a modell és a kísérlet közötti legjobb egyezés megtalálására használják. Az adatsorok közötti különbséget egy olyan becslő segítségével számszerűsítjük, mint az átlagos négyzetes hiba (MSE). Az ismeretlen tulajdonságokat addig változtatjuk, amíg a minimális MSE-t el nem érjük. Ez azt jelenti, hogy a legkisebb MSE egyenértékű a legjobb válasszal.
Nézze meg az alábbi ábrán az MSE görbét a filmvastagság függvényében egy szilíciumra felvitt átlátszó film esetében. A legalacsonyabb MSE-érték 749 nm-es vastagságnál jelentkezik, számos helyi minimum ellenére. Így a helyes filmvastagság szintén 749 nm. A regressziós algoritmus egy lokális minimumot tekinthet helyesnek. A helyes globális minimum meghatározásához tehát célszerű szemrevételezéssel összehasonlítani a legalacsonyabb MSE eredményeit.
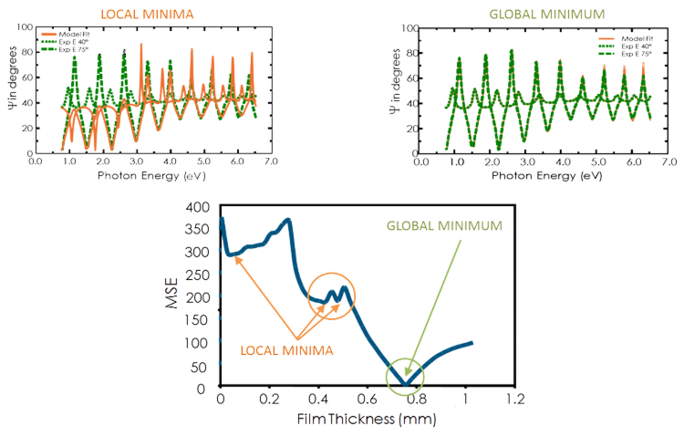
11. ábra, jobb felső sarok: Kísérleti adatok és a modellhez generált megfelelő görbék a globális minimumon. 11. ábra, balra fent: A 0,45 µm vastagság közelében lévő lokális minimumnál egy hasonló görbe könnyen felismerhető, mint hibás eredmény. 11. ábra, alul: Az MSE görbe a vastagság függvényében mutatja a globális minimumot. A regressziós algoritmus helyi minimumokat adhat, de nem a végső eredményt.
A filmvastagságot általában a felületről visszaverődő fény és a filmen áthaladó fény interferenciája alapján határozzák meg. Az, hogy ez az interferencia konstruktívnak vagy destruktívnak tekinthető-e, a felületi visszaverődéshez csatlakozó fény relatív fázisától függ. Az interferencia amplitúdó- és fázisinformációt egyaránt tartalmaz. A Δ fázisinformáció nagyon érzékeny a filmekre, egészen a monoréteg alatti vastagságig. Lásd az alábbi ábrán a visszavert intenzitás és az ellipszometria összehasonlítását ugyanarra a sorozatra vékony SiO2 rétegek Si-n. A visszaverődési erősség minden egyes film esetében közel azonos, míg a Δ-ben nagy eltérések vannak.
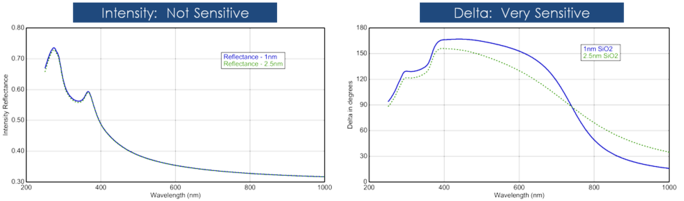
12. ábra, balra: Visszaverődési intenzitás és ellipszometriai delta (jobbra) két vékony oxidra szilíciumon. Az intenzitásmérés nem mutatja, hogy a delta nagyon érzékeny a nanométeres méretű filmekre.
Az ellipszometriát általában szubnanométeres és néhány mikron vastagságú filmeknél használják. Néhány tíz mikronnál vastagabb filmeknél az interferencia-ingadozás csak egyre nehezebben oldható fel, kivéve, ha hosszabb infravörös hullámhosszakat használnak. Ezért vastagabb filmeknél általában más mérési technikákat alkalmaznak.
A vastagság méréséhez a fény egy részének át kell haladnia a teljes filmen, majd vissza kell térnie a felületre. Fényelnyelő anyagok esetén az optikai vastagságmérés csak vékony és félig átlátszatlan rétegeken végezhető, kivéve, ha olyan spektrális tartományokban végzik, ahol kisebb az elnyelés. Például egy szerves film, amely elnyeli az UV- és IR-fényt, a közép-látható hullámhosszakon átlátszó lehet. A fémek minden hullámhosszon erősen elnyelnek, így a maximálisan meghatározható rétegvastagság 100 nm körül van.
Optikai állandók
A vastagságméréseknél fontos szerepet játszanak az optikai állandók. A film vastagsága befolyásolja a filmben áthaladó fény úthosszát, az index pedig a fényhullám sebességét és törési szögét. Mindkettő hozzájárul tehát a filmben áthaladó fény és a felületi visszaverődés közötti késleltetéshez. Az n és k, valamint a vastagság meghatározása szükséges ahhoz, hogy az optikai mérésből helyes eredményeket kapjunk.
Mivel egy anyag optikai állandói különböző hullámhosszakra változnak, az ellipszométerrel elemzett összes hullámhosszt egyedileg kell meghatározni. Az anyag válaszát az egyes hullámhosszakon az optikai állandók táblázatának segítségével lehet megjósolni. Az ismeretlen optikai állandók hullámhosszonkénti fáradságos beállításának elkerülése érdekében előnyös az összes hullámhossz egyidejű használata. A diszperziós reláció állítható paraméterei például lehetővé teszik, hogy a teljes optikai állandó alakja megfeleljen a kísérleti eredményeknek. Az egyes n és k értékek hullámhosszonkénti beállításához képest jelentősen csökken az ismeretlen szabad paraméterek száma.
A Cauchy- vagy Sellmeier-összefüggéseket gyakran használják az átlátszó anyagok indexének leírására, ahol a Cauchy-összefüggés általában a következőképpen adódik:
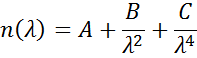
a három tagot az anyag törésmutatójának megfelelően illesztve. A Cauchy-összefüggést nem korlátozza a Kramers-Kronig (KK) konzisztencia, és nem fizikai diszperzióhoz vezethet. A Sellmeier-reláció viszont Kramers-Kronig (KK) konzisztenciát ír elő, ami biztosítja, hogy az optikai diszperzió reális alakot tartson. A Sellmeier-relációt jellemzően így írják fel:
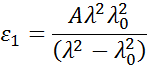
Az elnyelő anyagoknak gyakran van egy átlátszó hullámhosszú tartománya, amely a Cauchy- vagy Sellmeier-relációval modellezhető. Míg az elnyelő tartományban azonban figyelembe kell venni a valós és a képzeletbeli optikai állandókat is. A különböző anyagok abszorpciójának leírására számos diszperziós reláció használja az oszcillátorelméletet, beleértve a Lorentz-, a Harmonic- és a Gauss-elméletet. Mindegyiknek hasonló tulajdonságai vannak, az abszorpciós jellemzőket az Amplitúdóval, a kiszélesedéssel és a középponti energiával (a fény frekvenciájával kapcsolatban) írják le. A valós komponens alakját a Kramers-Kronig-konzisztencia segítségével számítják ki, miután az imaginárius viselkedést az oszcillátor leírja. A mért spektrális tartományon túli esetleges extra abszorpció figyelembevétele érdekében a valós komponenshez egy eltolás kerül hozzáadásra. A Lorentz-oszcillátor a következőképpen írható fel:
![]()
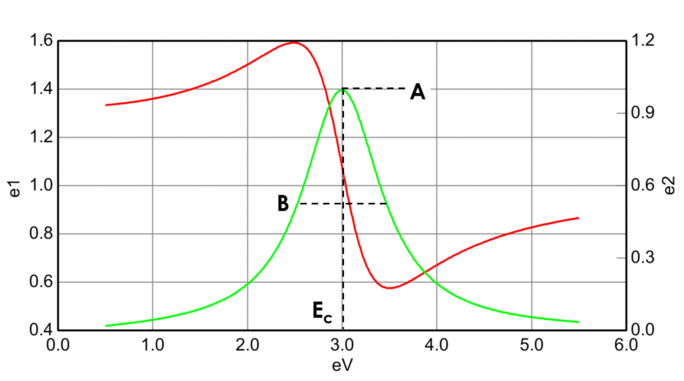
A 13. ábrán az amplitúdó (A), a szélesedés (B), a centrális energia (Ec) és az eltolás (e1, off set) is látható egy tipikus Lorentz-oszcillátor esetében. Az E energia a hullám frekvenciájához, n-hez viszonyítva:
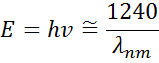
A h Planck-állandó és a λ hullámhossz nanométerben van megadva. Más diszperziós modellek, mint például a Tauc-Lorentz és a Cody-Lorentz, tartalmaznak a sávhézag energiáját leíró kifejezéseket.
További olvasmány
Az ellipszometria egy bevett optikai technika a vékonyrétegek és az ömlesztett anyagok mérésére. Az anyagszerkezetről történő reflexió/transzmisszió által okozott polarizációs változásokat használja az anyag jellemzőinek, például a vastagságnak és az optikai állandóknak a meghatározására.
Aspnes D.E. (1985). Az optikai tulajdonságok pontos meghatározása ellipszometriával. In: Palik E.D. (szerk.) Handbook of Optical Constants of Solids, pp. 89-112. Academic Press, Orlando.
Azzam R.M.A. és Bashara N.M. (1987). Ellipsometry and Polarized Light, Elsevier Science B.V., Amsterdam, The Netherlands.
Boccara A.C., Pickering C. és Rivory J. (szerk.), (1993). Spectroscopic Ellipsometry, Elsevier Publishing, Amsterdam.
Collins R.W., Aspnes D.E., and Irene E.A. (eds.), (1998). “Proceedings from the Second International Conference on Spectroscopic Ellipsometry” (A spektroszkópiai ellipszometria második nemzetközi konferenciájának jegyzőkönyve). In: Thin Solid Films, vols. 313-314.
Fujiwara H., Spectroscopic Ellipsometry, Principles and Applications, John Wiley & Sons, Ltd. (Vékony szilárd filmek, 313-314. kötet). 2007
Gottesfeld S., Kim Y.T., and Redondo A. (1995). “Az ellipszometria és a spektroellipsometria legújabb alkalmazásai elektrokémiai rendszerekben”, In: I. Rubinstein (szerk.), Fizikai elektrokémia: Principles, Methods, and Applications, Marcel Dekker, New York.
Herman, I.P. (1996). Optical Diagnostics for Thin Film Processing, pp 425-479. Academic Press, San Diego, California.
Johs B. et al (1999). “Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part II: Advanced Applications”. Optical Metrology, vol. CR72, pp 29-58. SPIE, Bellingham, Washington.
Johs B. et al (2001). “Recent Developments in Spectroscopic Ellipsometry for in situ Applications”. In: Duparré A, Singh B (szerk.) Optical Metrology Roadmap for the Semiconductor, Optical, and Data Storage Industries II, vol. 4449, pp 41-57. SPIE, Bellingham, Washington.
Roseler A. (1990). Infrared Spectroscopic Ellipsometry, Akademie-Verlag, Berlin.
Rossow U. és Richter W. (1996). “Spektroszkópiai ellipszometria” in: Bauer G and Richter W (eds.) Optical Characterization of Epitaxial Semiconductor Layers, pp. 68-128, Springer-Verlag, Berlin.
Tompkins H.G. (1993). A User’s Guide to Ellipsometry, Academic Press, San Diego, California.
Tompkins H.G. és McGahan W.A. (1999). Spectroscopic Ellipsometry and Reflectometry, John Wiley & Sons, Inc., USA.
Tompkins, H.G. és Irene E.A. (szerk.), 2005, Handbook of Ellipsometry, William Andrew Publishing, New York.
Tompkins, H. G. és Hilfiker, J. H., Spectroscopic Ellipsometry, Practical Application to Thin Film Characterization, 2016, Momentum Press Engineering
Woollam J.A. és Snyder P.G. (1992). “Variable Angle Spectroscopic Ellipsometry” in: Brundle CR, Evans CA és Wilson S (szerk.) Encyclopedia of Materials Characterization: Surfaces, Interfaces, Thin Films, pp. 401-411, Butterworth-Heinemann, Boston.
Woollam J.A. et al (1999). “Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part I: Basic Theory and Typical Applications”. Optical Metrology, vol. CR72, pp 3-28. SPIE, Bellingham, Washington.
Woollam J.A. (2000). “Ellipszometria, változó szögű spektroszkópia” in: Webster J.G. (szerk.) Wiley Encyclopedia of Electrical and Electronics Engineering, pp. 109-116. John Wiley & Sons, New York.