Mi a meredekség-metszet forma

A meredekség-metszet forma egyike annak a három formának, amit egy egyenes kifejezésére használhatunk. A többi formát pont-lejtő formának és standard formának nevezzük, de ebben a részben többnyire a lejtőmetszet formát fogjuk használni. A meredekség-metszet formát használva egy egyenes egyenletét úgy fejezzük ki, hogy:

y=mx+by = mx + by=mx+b

Az xxx és yyy értékeket a grafikon egy pontjának koordinátáiként ismerheted, de mi az az mmm és bbb?

Mi a b az y=mx+b-ben?

A b betű egy szám, amely azt jelenti, hogy az egyenes mikor érinti az y tengelyt. Ezt nevezzük az y metszéspontnak is. Rajzoljunk például egy egyenest a koordinátasíkra.

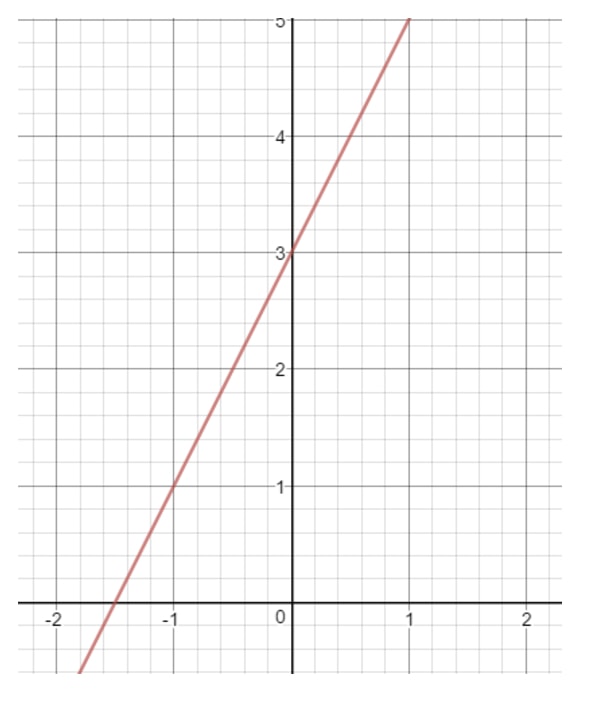
Ha jobban megnézzük az y-tengelyt, az egyenes egy bizonyos helyen érinti az y-tengelyt. Hol van ez a hely? Ez lenne a 3-as szám, mert ott metszi egymást az y-tengely és az egyenes. Ez azt jelenti, hogy arra következtethetünk, hogy b = 3.

Mi az m a meredekség metszéspont alakban?

Az m betű egy szám, amely az egyenes meredekségét jelöli. Vannak, akik a meredekséget emelkedésnek nevezik. Emlékezzünk vissza, hogy ha van két pontunk, akkor a két pont meredekségét a meredekségi képlet segítségével tudjuk megkeresni

m=riserun=y2-y1x2-x1m = \frac{rise}{run} = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}m=runrise=x2-x1y2-y1

Az ötlet itt is működik. Ha egy egyenes bármely két pontját vesszük, akkor a fenti képlet segítségével meg tudjuk találni az egyenes meredekségét! Vegyük például ezt az egyenest.

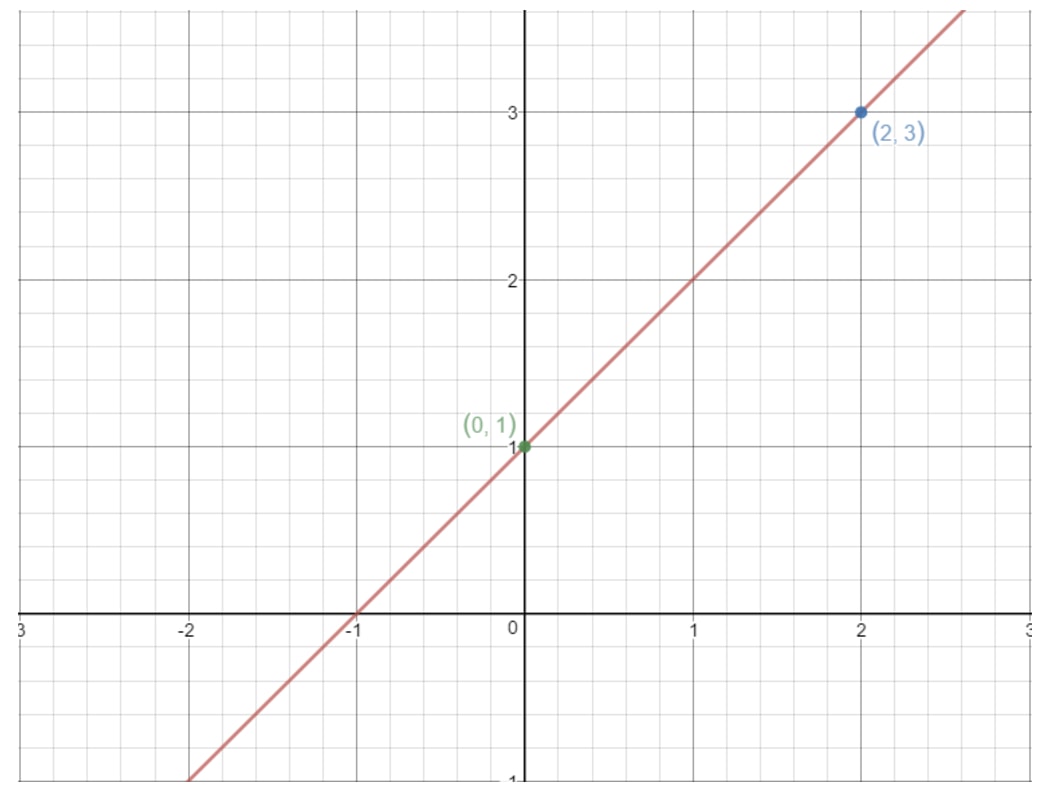
Megjegyezzük, hogy a (2, 3) és (0, 1) pontok ezen a grafikonon vannak. Miért nem használjuk tehát ezt a két pontot az egyenes meredekségének meghatározásához? A képletet használva megkapnánk:

m=y2-y1x2-x1=1-30-2m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}} = \frac{1 – 3}{0 – 2}m=x2-x1y2-y1=0-21-3=-2-2= \frac{-2}{-2}=-2-2-2=1= 1=1

Ez azt jelenti, hogy ennek az egyenesnek a meredeksége 111!

A meredekség különlegessége, hogy az egyenes bármely két pontjából meg tudjuk találni. Tehát ha két különböző pontot vennénk ezen az egyenesen, akkor is azt kapnánk, hogy a meredeksége 111.

Hogyan írjunk egyenletet meredekség-metszet formában?

Tudhatod, hogy néz ki a meredekség-metszet forma, de az esetek felében olyan egyenleteket kapsz, amelyek nem ebben a formában vannak. Így a te feladatod, hogy átfordítsd lejtőmetszet formába. Hogyan csináljuk ezt? A cél az, hogy mindig izoláljuk az yyy kifejezést. Tegyük fel például, hogy a következő egyenletet kapod

6x+4+2y=06x + 4 + 2y = 06x+4+2y=0

az yyy tag izolálása, áthelyezzük a 6x+46x + 46x+4-et az egyenlet jobb oldalára

2y=-6x-42y = -6x – 42y=-6x-4

Most a 222 az yyy útjában van, ezért megszabadulunk tőle úgy, hogy az egyenlet mindkét oldalát elosztjuk 222-vel.

2y2=-6x-42\frac{2y}{2} = \frac{-6x – 4}{2}22y=2-6x-4y=-6×2-42y = -\frac{6x}{2}{2} – \frac{4}{2}y=-26x-24y=-3x-2y = -3x – 2y=-3x-2

Mivel yyy izolált, láthatjuk, hogy az y=mx+by = mx + by=mx+b merőleges metszet alakban van, ahol m=-3m = -3m=-3, és b=-2b = -2b=-2.

Most, hogy már nagyon jól ismerjük az y metszéspontját és meredekségét, miért nem nézzük meg a megtalálásukkal kapcsolatos konkrét kérdéseket!

Hogyan találjuk meg az y metszetet?

Kérdés 1: Az y=12x+5y = \frac{1}{2} x + 5y=21x+5 lineáris egyenlet segítségével találjuk meg az y metszetet.

Megjegyezzük itt, hogy az egyenlet már a meredekség-metszet formában y=mx+by = mx + by=mx+b. Már csak azt kell kitalálnunk, hogy mi a bbb. Láthatjuk, hogy b=5b = 5b=5, tehát az y metszete 555.

Lássunk egy kicsit nehezebb kérdést.

Kérdés 2: Határozzuk meg a 2x-4y=82x – 4y = 82x-4y=8

Most ez a lineáris egyenlet nem meredekség-metszet formában van, ezért először át kell alakítanunk ebbe a formába. A célunk az, hogy ebben az egyenletben elkülönítsük yyy-t.

Lássuk, hogy ha a 2x2x2x-et áthelyezzük az egyenlet jobb oldalára, akkor:

-4y=8-2x-4y = 8 – 2x-4y=8-2x

Most ha mindkét oldalt elosztjuk -4-4-4-gyel, akkor megkapjuk:

-4y-4=8-2x-4\frac{-4y}{-4} = \frac{8 – 2x}{-4}-4-4-4y=-48-2xy=8-4-2x-4y = \frac{8}{-4}{-4} – \frac{2x}{-4}y=-48–42xy=-2+12xy = -2 + \frac{1}{2}xy=-2+21x

Most a két tag helyzetét felcserélve megkapjuk:

y=12x-2y = \frac{1}{2}x – 2y=21x-2

Kérdés 3: Határozzuk meg a 4y-8=04y – 8 = 04y-8=0 y metszéspontját.

Ez egy kicsit furcsán nézhet ki, mert nincs xxx kifejezés, de a célunk ugyanaz marad. El fogjuk különíteni az yyy-t.

Az egyenlet jobb oldalára áthelyezve a -8-8-8-at megkapjuk:

4y=84y = 84y=8

Az egyenlet mindkét oldalát 444-gyel osztva megkapjuk

4y4=84\frac{4y}{4} = \frac{8}{4}44y=48y=2y = 2y=2

Most ez talán nem úgy tűnik, de az egyenlet meredekség-intercept formában van. Csakhogy m=0m = 0m=0, tehát az egész mxmxmxmx kifejezés eltűnt. Csak írjuk át az egyenletet így

y=0m+2y = 0m + 2y=0m+2

A megfigyelésből megállapíthatjuk, hogy b=2b = 2b=2, és így az y metszéspont 222. Végezzünk még egy kérdést.

4. kérdés: Határozzuk meg (ha lehetséges) az 5x-15=05x – 15 = 05x-15=0 y metszéspontját.

Ez azért érdekes, mert az egyenletben nincs yyy tag. Hogyan kellene tehát a lejtőmetszet formájába öntenünk? Nos, az egyetlen dolog, amit most tehetünk, az az xxx-re való izolálás, úgyhogy egyelőre próbáljuk meg ezt.

A 151515-öt az egyenlet jobb oldalára áthelyezve megkapjuk:

5x=155x = 155x=15

Az egyenlet mindkét oldalát elosztva megkapjuk:

5×5=155\frac{5x}{5} = \frac{15}{5}55x=515x=3x = 3x=3

Most ezt rajzoljuk fel egy grafikonra. Figyeljük meg, hogy ebben az egyenletben xxx kénytelen 333 lenni, és nem lehet más. Azonban yyy-ról nem mond semmit, így yyy bármi lehet. Ha felírnánk egy értéktáblázatot, akkor a következőket kapnánk:

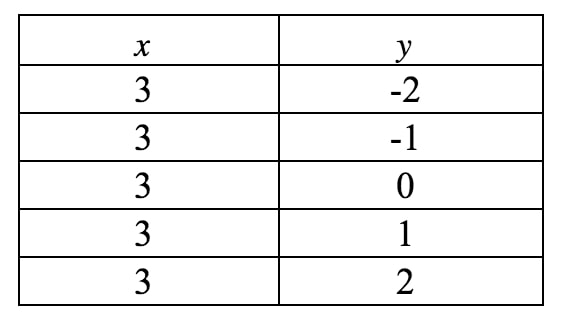
Ha ezeket a pontokat egy koordinátasíkra ábrázoljuk és megrajzoljuk az egyenest, akkor a következőket kapjuk:

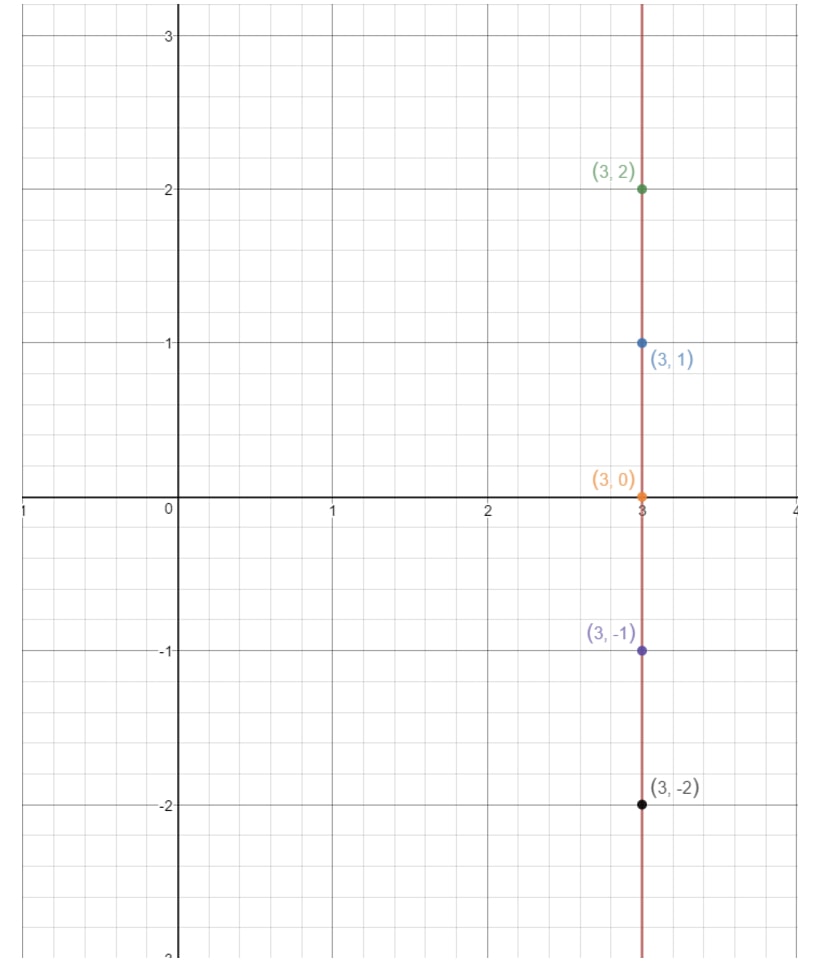
Észrevehetjük, hogy az egyenes soha nem érinti az y tengelyt. Ez azt jelenti, hogy az egyenletnek nincs y metszéspontja. Most, hogy az y metszéspont megtalálásának minden esetét lefedtük, nézzük meg azokat a kérdéseket, amelyek a meredekség megtalálását kérik!

Hogyan találjuk meg egy egyenlet meredekségét?

Kérdés 5: Keressük meg az y=32x+1y = \frac{3}{2}x + 1y=23x+1

Kérdés 6: Határozzuk meg a 6x-6y=06x – 6y = 06x-6y=0

Mint láthatjuk, az egyenlet nem meredekség-metszet formában van, ezért először át kell alakítanunk ebbe a formába. Célunk az yyy izolálása.

Az egyenlet jobb oldalára áthelyezve 6x6x6x6x-et kapjuk:

-6y=-6x-6y = -6x-6y=-6x

Elosztva mindkét oldalt -6-6-6-6-al kapjuk:

-6y-6=-6x-6\frac{-6y}{-6} = \frac{-6x}{-6}-6-6-6y=-6-6xy=xy = xy=x

Megjegyezzük, hogy ez valójában ferde metszet formában y=mx+by = mx + by=mx+b. Csakhogy az y metszéspont bbb ebben az esetben 000, xxx pedig megegyezik az 1x1x1x-el. Így átírhatjuk az egyenletet:

y=1x+0y = 1x + 0y=1x+0

Most megfigyelve látjuk, hogy m=1m = 1m=1. Mivel mmm a meredekség, ezért a meredekségnek 111-nek kell lennie. Csináljunk egy kicsit nehezebbet

7. kérdés: Határozzuk meg a 2y-4=02y – 4 = 02y-4=0

Ez megint egy kicsit furcsa, mert nincs xxx kifejezésünk. A célunk azonban, hogy elkülönítsük yyy-t, ugyanaz marad.

A -4-4-4-et az egyenlet jobb oldalára áthelyezve megkapjuk:

2y=42y = 42y=4

Az egyenlet mindkét oldalát 222-vel osztva megkapjuk:

2y2=42\frac{2y}{2} = \frac{4}{2}22y=24y=2y = 2y=2

Lássuk, hogy itt már meredekség-metszet formában van, csak az mxmxmx kifejezés rejtve van, mert m=0m = 0m=0. Tehát átírhatjuk az egyenletünket így:

y=0x+2y = 0x + 2y=0x+2

Mivel m=0m = 0m=0, akkor nulla a meredekségünk. Ha kíváncsi vagy, hogy néz ki egy 000 meredekségű egyenes, akkor itt van egy grafikon, amit megnézhetsz.

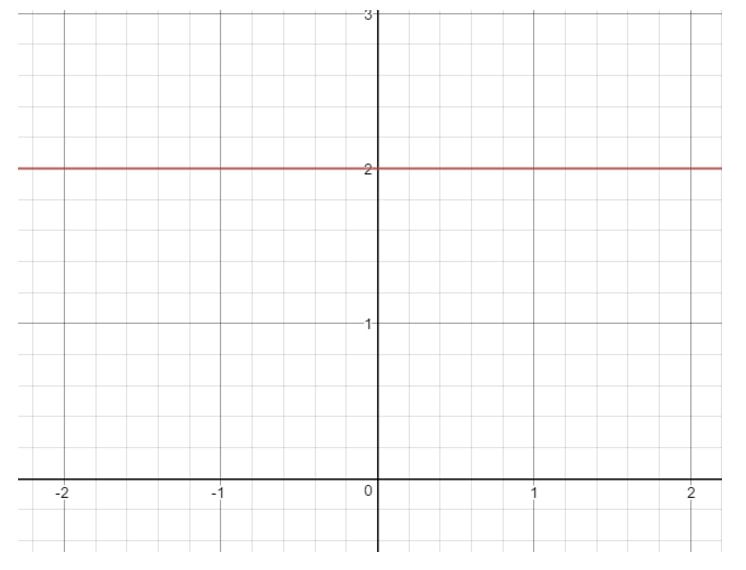
Kérdés 8: Találd meg (ha lehetséges) a 16-4x=016 – 4x = 016-4x=0

Ez esetben yyy nem izolálható, mert nincs yyy tag. Így csak annyit tehetünk, hogy xxx-et izoláljuk.

Az egyenlet jobb oldalára 161616-ot áthelyezve megkapjuk:

-4x=-16-4x = -16-4x=-16

Elosztva mindkét oldalt -4-4-4-4-gyel, megkapjuk:

-4x-4=-16-4\frac{-4x}{-4} = \frac{-16}{-4}-4-4-4x=-4-16x=4x = 4x=4

Ez még mindig nem a meredekség metszet formájában van, így az egyetlen reményünk a meredekség elérésére az, hogy megrajzoljuk ennek az egyenesnek a grafikonját. Ismét azt látjuk, hogy xxx mindig kénytelen 444 lenni, de yyy bármi lehet, mert nincs yyy kifejezés. Ha felírnánk egy értéktáblázatot, akkor azt kapnánk:

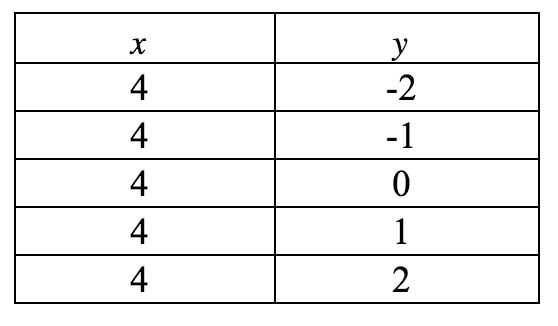
Ha ezeket a pontokat egy koordinátasíkon ábrázoljuk és megrajzoljuk az egyenest, akkor azt kapjuk:

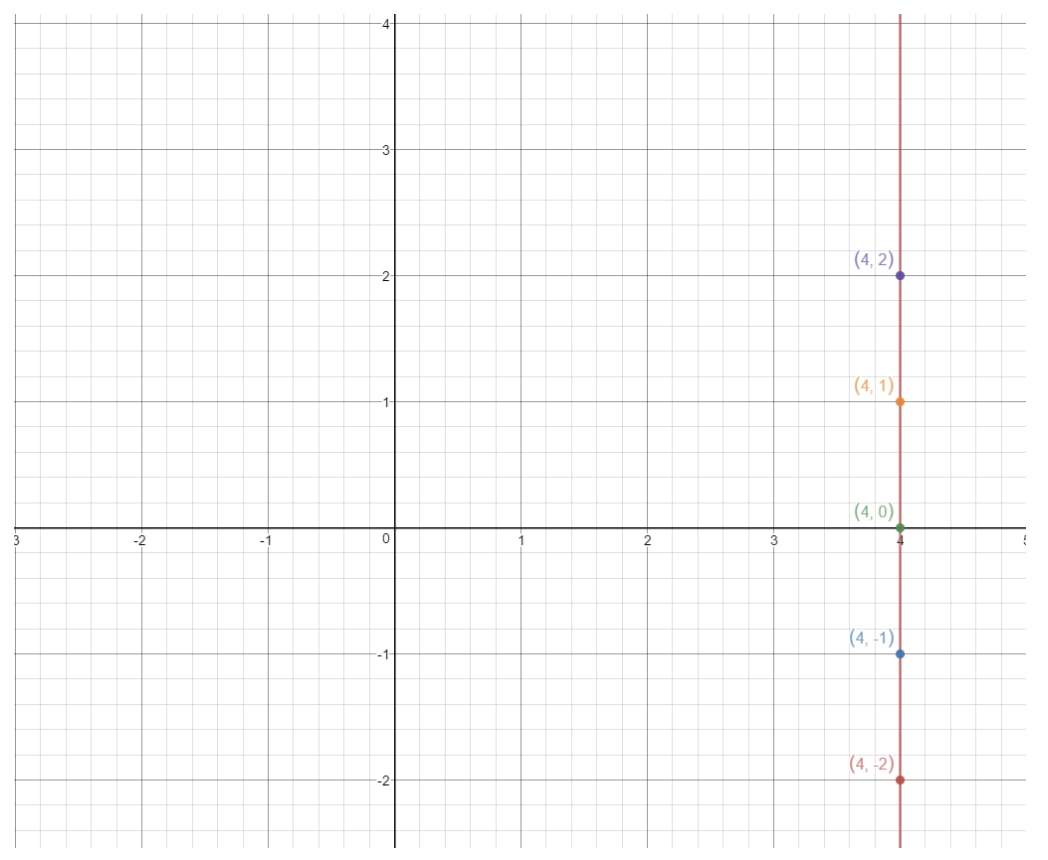
Ez egy függőleges vonal. Mi tehát a függőleges egyenes meredeksége? Próbáljuk meg ezt kitalálni az emelkedés és a lefutás megkeresésével. Nézd meg, hogy ez az egyenes mindig végtelenül emelkedik, de egyáltalán nincs lefutása. Tehát ez azt jelenti, hogy a futás 000. Ha tehát kiszámítjuk a meredekséget, akkor azt kapjuk:

m=futásfutás=emelkedés0=definedm = \frac{emelkedés}{futás} = \frac{emelkedés}{0} = undefinedm=futásemelkedés=0emelkedés=undefined

Nem tudunk osztani 000-zel, tehát valójában definiálatlan meredekségünk van.

Mi az a határozatlan meredekség?

A határozatlan meredekség olyan meredekség, amely egyenesen megy felfelé a grafikonon. Ahogy a fenti grafikonon látható, a lejtő végtelenül emelkedik, és nincs lefutása. Ennek eredményeként egy határozatlan meredekséget kapunk, mert nem tudunk osztani 000-zel.

Általában mindig határozatlan meredekséget kapunk, amikor egy egyenes függőleges egyenest kapunk!

Nézzünk meg néhány más egyedi kérdést!

Egyenletet találni egy pontból

Kérdés 9: Egy (2, 6) ponton áthalad az y=-5x+by = -5x + by=-5x+b egyenlet. Keressük meg a “bbb” értéket.

6=-5(2)+b6 = -5(2) + b6=-5(2)+b

Izolálva és megoldva bbb-re kapjuk:

6=-10+b6 = -10 + b6=-10+bb=16b = 16b=16

Megjegyezzük, hogy bbb az y metszéspontja is, tehát az y metszéspontja is 16161616!

Függvény meredekségének meghatározása két pontból

10. kérdés: Adott két pont (6, 1) és (-10, 9), találjuk meg az egyenes meredekségét.

Emlékezzünk arra, hogy az egyenes meredekségének meghatározásához a meredekség egyenletét használjuk

m=y2-y1x2-x1m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}m=x2-x1y2-y1

Ezzel a képlet használatával megkapjuk:

m=9-1-10-6=8-16m = \frac{9 – 1}{-10 – 6} = \frac{8}{-16}m=-10-69-1=-168

=1-2= \frac{1}{-2}=-21

Mi van, ha helyette egy egyenes teljes egyenletét kell megtalálnunk?

Egy egyenes egyenlete adott két pontban

Kérdés 11: Adott két pont (-6, 1) és (2, 6), találjuk meg a meredekség metszéspont alakú egyenletét.

Lényegében az y=mx+by = mx + by=mx+b alakú egyenletet próbáljuk megtalálni. Ehhez meg kell keresnünk mmm és bbb.

Emlékezzünk arra, hogy mmm megtalálásához a meredekségegyenletet használjuk

m=y2-y1x2-x1m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}m=x2-x1y2-y1

Ezzel a képlettel számolva megkapjuk:

m=6-12-(-6)=58m = \frac{6 – 1}{2 – (-6)} = \frac{5}{8}m=2-(-6)6-1=8558\frac{5}{8}85

Így most már megvan az egyenlet

y=58x+by = \frac{5}{8}x + by=85x+b

Most meg kell keresnünk bbb-et. A bbb megoldásához válasszuk ki a megadott pontok valamelyikét, és dugjuk be az egyenletbe. Ezt megtehetjük, mert mindkét pont az egyenesen fekszik, és az egyenes bármelyik pontja kielégítené az egyenletet. Használjuk a (2, 6) pontot. Lássuk, hogy:

6=58(2)+b6 = \frac{5}{8}(2) + b6=85(2)+b

A bbb izolálása adja:

6=108+b6= \frac{10}{8} + b6=810+bb=6-108b = 6 – \frac{10}{8}b=6-810b=488-108b = \frac{48}{8}{8} – \frac{10}{8}b=848-810b=388b = \frac{38}{8}b=838

Ezt tizedesjegyekben kifejezve megkapjuk, hogy b=4,75b = 4,75b=4,75. Így a meredekség-intercept formájú egyenletünk:

y=58x+4.75y = \frac{5}{8}x + 4.75y=85x+4.75

Az utolsó dolog, amivel ebben a részben foglalkozunk, az egyenes tartományának és tartományának megtalálása.

Hogyan találjuk meg a tartományt és a tartományt?

Az egyenes tartományának megtalálásához alapvetően ezt a kérdést tesszük fel magunknak: mi lehet xxx? Ha xxx lehet ezek az értékek, akkor hozzáadjuk őket a tartományhoz.

A tartományra ugyanez vonatkozik. Mi lehet yyy? Ha yyy lehetnek ezek az értékek, akkor hozzáadjuk őket a tartományhoz. Nézzünk egy példát.

12. kérdés: Keressük meg az y=2x+1y = 2x + 1y=2x+1 egyenlet tartományát és tartományát.

Megjegyezzük, hogy ha megrajzoljuk ennek az egyenesnek a grafikonját, akkor azt kapjuk:

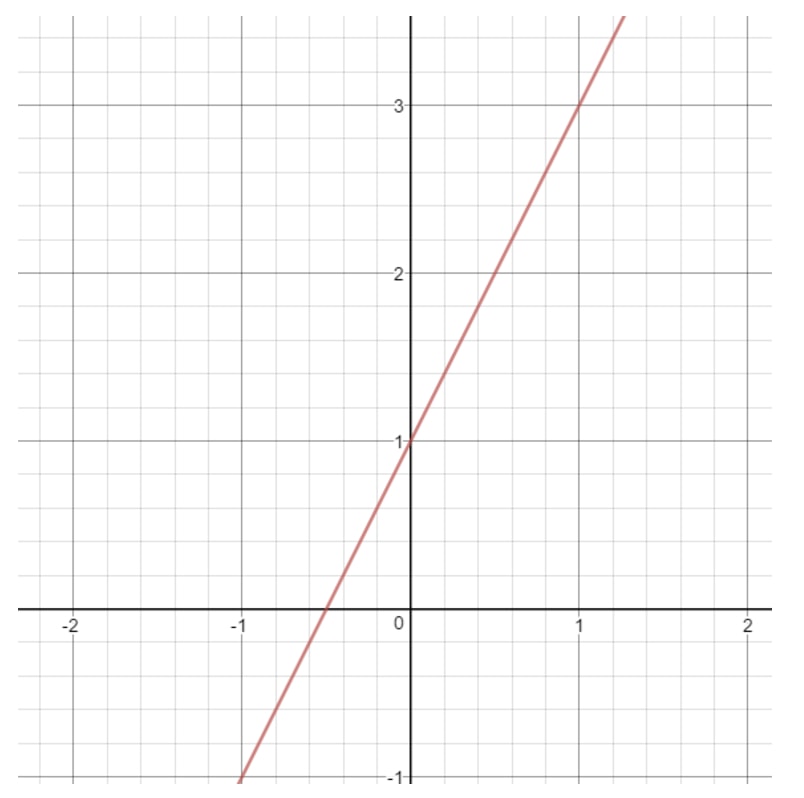
Mi lehet xxx ebben az egyenesben? Vegyük észre, hogy xxx bármi lehet, mert bármilyen xxx értékkel kaphatunk olyan pontot, amely az egyenesre esik. Ugyanez vonatkozik az y-ra is. Mindig választhatunk egy olyan yyy értéket, amely egy egyenesen lévő pontot ad. Tehát azt mondjuk, hogy

Domain: {x∈\in∈R}Tartomány: {y∈\in∈R}

ahol R az “összes valós számot” jelenti. Végezzünk egy nehezebbet.

13. kérdés: Keressük meg az y=-2y = -2y=-2 egyenlet tartományát és tartományát.

Ha most ezt az egyenest grafikonra rajzoljuk, akkor megkapjuk:

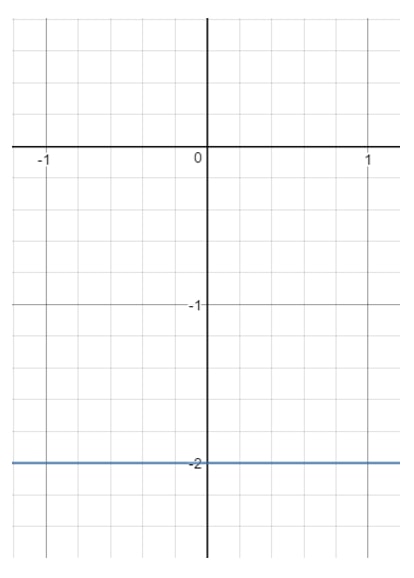
Megjegyezzük, hogy xxx bármi lehet, mert bármilyen xxx értékkel kaphatunk olyan pontot, ami az egyenesen van, amíg y=-2y = -2y=-2. Viszont nézzük meg az yyy-t. Látod, hogy yyy kénytelen -2-2-2-2 lenni, és nem lehet más. Abban a pillanatban, hogy más yyy értéket választunk (például 111-et), akkor az a pont kikerül az egyenesből. Ez tehát azt jelenti, hogy:

Domain: R}Tartomány: {x ∈\in∈ R}Tartomány: {y = -2}

Kérdés 14: Keressük meg az x=1x = 1x=1 egyenlet tartományát és tartományát.

Ha most ezt az egyenest grafikonra rajzoljuk, akkor azt kapjuk:

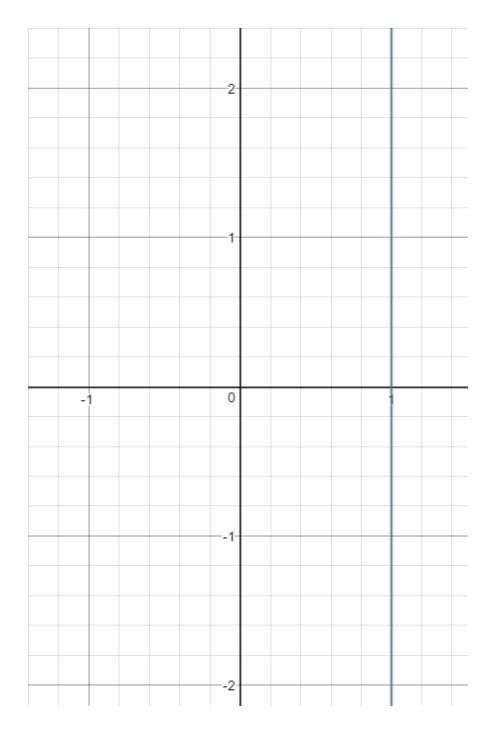
Láthatjuk, hogy xxx kénytelen 111 lenni, és nem lehet más. Abban a pillanatban, hogy egy másik xxx értéket választasz (például 222), akkor az a pont kikerül az egyenesből. yyy-t azonban nézd meg. Vegyük észre, hogy yyy bármi lehet, mert bármilyen yyy értékkel kaphatunk olyan pontot, amely az egyenesen van, amíg x=1x = 1x=1

Ez tehát azt jelenti:

Domain: {x=1}Tartomány: { https://www.desmos.com/calculator/2rnqgoa6a4

Megtanít arra, hogyan kell egy lineáris egyenletet grafikusan ábrázolni. Mindössze annyit kell tenned, hogy beírod az mmm és a bbb értékeit. Ezután automatikusan megrajzolja neked az egyenest! Ez akkor is hasznos, ha a meredekség metszéspont alakját próbálod megtalálni.