A folyadékokban úszkáló kis Reynolds-számú úszókhoz való hasonlóságtól inspirálva létrehoztuk az első ellenállásos erőelméletet szemcsés közegekre az erők és a mozgás előrejelzésére. A kulcsötlet a szuperpozíció elve: a szemcsés közegben tetszőleges pálya mentén mozgó, összetett alakú testekre és lábakra ható erők jól közelíthetők az egyes elemeikre ható erők szuperpozíciójával (1. ábra). Az integrációs elv érvényes az alacsony Reynolds-számú úszókra, mert mivel a tehetetlenségi hatások elhanyagolhatóak, az elemek körüli folyadékáramlás eléggé lokális ahhoz, hogy az elemre ható szemcsés erő független legyen a többi elemre ható erőtől. Ezt figyelembe véve feltételeztük, hogy az ellenállásos erőelmélet szemcsés közegekre is működik.

1. ábra. Az ellenállásos erőelmélet szuperpozíciós elve.

Az ellenállásos erő mérése

Mivel az állatok és a robotok összetett morfológiával és kinematikával rendelkeznek, testük és lábaik egyes elemei nemcsak különböző mélységben lehetnek, hanem különböző orientációkkal és mozgásirányokkal is rendelkezhetnek (1. ábra, balra). A folyadékokban úszó, alacsony Reynolds-számú úszók esetében a Stokes-törvényből levezethető, hogy az erő hogyan függ az orientációtól és az iránytól. A szemcsés közegek esetében azonban nem tudjuk, hogyan függ tőlük az erő, mert ilyen egyenletek nem léteznek. Ezért egy lemezelem segítségével elvégeztük az első méréseket a szemcsés erőkről a behatoló orientáció és irány függvényében (1. ábra, jobbra).

Megállapítottuk, hogy az erő (feszültség) érzékenyen függ az orientációtól és az iránytól is (2. ábra, balra). A függőleges erő akkor maximális, ha a lemez behatolója vízszintesen tájolt és lefelé hatol. Amint az orientáció eltér a vízszintestől és az irány eltér a lefelé irányulótól, a függőleges erő gyorsan csökken.

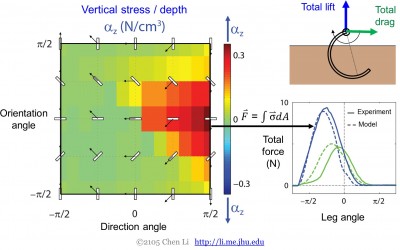
2. ábra. Ellenállási erőmérések és az elmélet validálása. Az egyszerűség kedvéért csak a függőleges ellenállási erőméréseket mutatjuk be.

Az ellenállási erő elmélet validálása

A szemcsés ellenállási erőméréseinket felhasználva integráltuk a lábelemekre ható feszültségeket, és felfedeztük, hogy az ellenállási erő elmélet jól megjósolja a szemcsés közegben mozgó robotlábra ható teljes felhajtó- és ellenállási erőket (2. ábra, jobbra). A szuperpozíció elvének köszönhetően a modell tetszőleges alakú és pályájú lábakra is pontos:

A rezisztív erőelmélet előrejelző ereje

Az ellenállási erőelméletet egy szemcsés közegen keresztül forgatott robotlábon (előírt kinematika) validálva, ezután egy szemcsés közegen szabadon mozgó roboton teszteltük előrejelző erejét. Egy egyedi lábú robotot futtattunk szemcsés közegeken a lépésfrekvencia és a lábgörbület széles tartományában. Mint korábban megállapítottuk, a robot gyorsabban mozog a konvex felületű lábakkal hátrafelé, mint előrefelé:

Ezután kidolgoztuk a robot többtestű dinamikai szimulációját, és az elemi erők integrálásával ellenállás-elméletet használtunk a robot testére és lábaira ható felhajtó- és ellenállási erők kiszámítására. Megállapítottuk, hogy az ellenállás-erőelméletet alkalmazó szimuláció által megjósolt mozgásdinamika jól illeszkedik a kísérleti megfigyelésekhez:

A kísérlet és a szimuláció összehasonlítása azt mutatta, hogy az ellenállás-erőelmélet pontosan és gyorsan képes megjósolni a lábak mozgását szemcsés közegen a lépésfrekvencia és a lábgörbület széles tartományában (3. ábra).

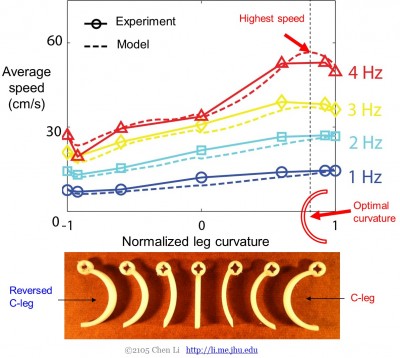
3. ábra. Az ellenállás-erőelmélet előrejelzi a lábakon járó robotok mozgását szemcsés közegeken.

Mivel az ellenállás-erőelméletünk lehetővé tette az erők és a mozgás kvantitatív előrejelzését szemcsés közegekben a folyadékok aero- és hidrodinamikájához hasonlóan, létrehoztuk az első terradinamikát áramló talajra.

A rezisztív erőelmélet általánossága

Végeztünk rezisztív erőméréseket különböző szemcseméretű, alakú, súrlódású, sűrűségű, tömörségű és polidiszperzitású szemcsés közegek sokféleségére. Megállapítottuk, hogy az erő függése a behatoló orientációjától és irányától feltűnően hasonló (4. ábra, balra).

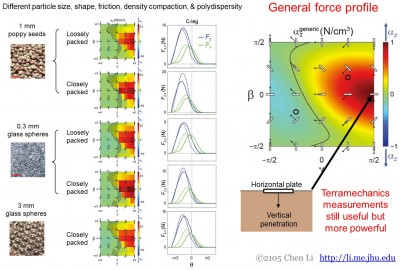
4. ábra. Az ellenállási erő elmélet általánossága a szemcsés közegek sokféleségére és gyakorlati haszna.

Ez jelentős gyakorlati előnyt jelent. Mivel ezek a szemcsés közegek ugyanolyan általános feszültségprofillal rendelkeznek, egyetlen erőmérés a maximális függőleges erő meghatározásához elegendő a többi orientációra és irányra vonatkozó erőkre való következtetéshez anélkül, hogy az összeset meg kellene mérni (4. ábra, jobbra). Ez egyszerűen elvégezhető egy kapható penetrométerrel. Ez azt is jelenti, hogy a terramechanikai vizsgálatok során kapott, vízszintes, lefelé penetráló lemezzel végzett mérések továbbra is felhasználhatók, de az ellenállási erőelmélet segítségével erőteljesebben.

Végezetül, a szuperpozíció elvének köszönhetően az ellenállási erőelméletünk elvileg tetszőleges morfológiájú és kinematikájú állatokra és eszközökre is alkalmazható (feltéve, hogy azok a kis sebességű, nem inerciális és kontinuus rezsimekben működnek). Például azt is felfedeztük, hogy az elmélet a vízszintes síkban végzett ellenállási erőméréseket felhasználva képes megjósolni a homoki gyík mozgását szemcsés közegben.

Miért nem működik a klasszikus terramechanika a marsjárók esetében

A klasszikus terramechanikában, mivel a nagy kerekek és pályák talajfelülete általában viszonylag sík és egyenletes, a szemcsés közegekben a függőleges behatolási erők csak egy vízszintes lemez lefelé történő mozgatásával (penetrométerrel) jellemezhetőek (5. ábra), de egy behatolóra más irányokban és orientációkban nem. Ezt azután a felhajtóerő előrejelzésére használják, amelyet aztán (statikusan és dinamikusan) a jármű tömegével egyensúlyozva a süllyedés előrejelzésére használnak.

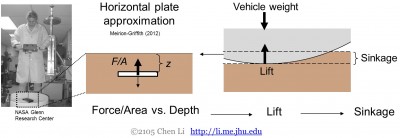
5. ábra. A klasszikus terramechanikai modellek fejlesztésénél elterjedt vízszintes lemez közelítés.

A laza szemcsés közegen mozgó roverek kis kerekei (vagy még nagyobb, elég mélyre süllyedt kerekek) esetében azonban a talajfelület erősen görbültté válik, a vízszintestől távol eső orientációkkal. Amint azt az összes orientációt és irányt figyelembe vevő ellenállási erőméréseinkkel kimutattuk, egy vízszintes lemezre általában sokkal nagyobb függőleges erő hat, mint egy vízszintestől távol esőre (2. ábra, balra). Ennek eredményeképpen a vízszintes lemez közelítése többé nem érvényes, és a klasszikus terramechanikai modellek jelentősen túlbecsülik a felhajtóerőt és alulbecsülik a süllyedést.

Hasonló publikációk:

1. Li C, Zhang T, Goldman DI (2013). A terradynamics of legged locomotion on granular media, Science, 339, 1408-1412 (Featured in Science Perspective) PDF
2. Ding, Y, Li C, Goldman DI (2013). Swimming in the desert, Physics Today, 66, 68-69 (Invited Paper) PDF
3. Maladen RD, Ding Y, Li C, Goldman DI (2009). Undulatory swimming in sand: subsurface locomotion of the sandfish lizard, Science, 325, 314-318 (Featured in Nature News & Views) PDF