by Marco Taboga, PhD
Egy esemény indikátorfüggvénye egy olyan véletlen változó, amely 1 értéket vesz fel, ha az esemény bekövetkezik, és 0 értéket, ha az esemény nem következik be. Az indikátorfüggvényeket gyakran használják a valószínűségelméletben a jelölések egyszerűsítésére és tételek bizonyítására.

Definíció
A következő egy formális definíció.
Definíció Legyen  egy mintatér és
egy mintatér és  egy esemény. Az
egy esemény. Az  esemény
esemény  jelű indikátorfüggvénye (vagy indikátor véletlen változója) a következőképpen definiált véletlen változó:
jelű indikátorfüggvénye (vagy indikátor véletlen változója) a következőképpen definiált véletlen változó: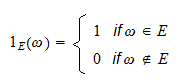
Míg a  esemény indikátorát általában
esemény indikátorát általában  -vel jelöljük, néha
-vel jelöljük, néha -vel is jelöljük, ahol
-vel is jelöljük, ahol  a görög Chi betű.
a görög Chi betű.
Példa Dobunk egy kockát, és az 1-től 6-ig terjedő hat szám közül az egyik megjelenhet képpel felfelé. A mintatér Definiáljuk az
Definiáljuk az  a “Egy páros szám jelenik meg képpel felfelé” mondat által leírt eseményt. A
a “Egy páros szám jelenik meg képpel felfelé” mondat által leírt eseményt. A  esemény indikátora egy olyan véletlen változó, amely 1 értéket vesz fel, ha páros szám jelenik meg képpel felfelé, és egyébként 0 értéket. Ennek az indikátornak az eseti definíciója
esemény indikátora egy olyan véletlen változó, amely 1 értéket vesz fel, ha páros szám jelenik meg képpel felfelé, és egyébként 0 értéket. Ennek az indikátornak az eseti definíciója
A fenti definícióból könnyen belátható, hogy  diszkrét véletlen változó, amelynek támasza
diszkrét véletlen változó, amelynek támasza  és valószínűségi tömegfüggvénye
és valószínűségi tömegfüggvénye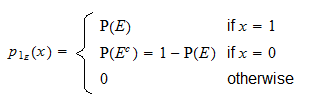
Tulajdonságai
Az indikátorfüggvények a következő tulajdonságokkal rendelkeznek.
Teljesítmények

 -adik hatványa egyenlő
-adik hatványa egyenlő  :
: mert
mert  lehet
lehet  vagy
vagy  és
és
Várható érték
A  várható értéke egyenlő
várható értéke egyenlő  :
: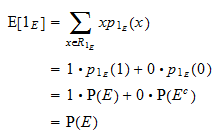
Variancia
A  szórása
szórása  . A szokásos szórásképletnek és a fenti hatványtulajdonságnak köszönhetően megkapjuk
. A szokásos szórásképletnek és a fenti hatványtulajdonságnak köszönhetően megkapjuk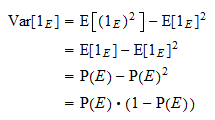
Összefüggések
Ha  és
és  két esemény, akkor
két esemény, akkor mert:
mert:
-
ha
 , akkor
, akkor  és
és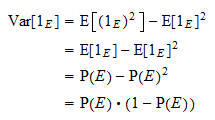
-
ha
 , akkor
, akkor és
és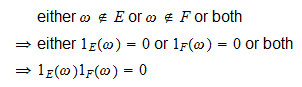
Nulla valószínűségű események jelzői
Legyen  egy nulla valószínűségű esemény és
egy nulla valószínűségű esemény és  egy integrálható véletlen változó. Akkor,
egy integrálható véletlen változó. Akkor, Míg ennek a ténynek a szigorú bizonyítása meghaladja e bevezető ismertetés kereteit, ennek a tulajdonságnak intuitívnak kell lennie. A
Míg ennek a ténynek a szigorú bizonyítása meghaladja e bevezető ismertetés kereteit, ennek a tulajdonságnak intuitívnak kell lennie. A  véletlen változó
véletlen változó  minden mintapontban egyenlő nullával, kivéve esetleg az E$” style=”background-position:0px -1174pxvertical-align:-5px”>-ben lévő
minden mintapontban egyenlő nullával, kivéve esetleg az E$” style=”background-position:0px -1174pxvertical-align:-5px”>-ben lévő  felvehető értékek súlyozott átlaga, ahol minden értéket a megfelelő valószínűséggel súlyozunk. A nem nulla értékek, amelyeket
felvehető értékek súlyozott átlaga, ahol minden értéket a megfelelő valószínűséggel súlyozunk. A nem nulla értékek, amelyeket  felvehet, nulla valószínűséggel súlyozottak, tehát
felvehet, nulla valószínűséggel súlyozottak, tehát  -nek nullának kell lennie.
-nek nullának kell lennie.
megoldott feladatok
Az alábbiakban néhány feladatot találsz magyarázott megoldásokkal.
1. gyakorlat
Tekintsünk egy  véletlen változót és egy másik véletlen változót
véletlen változót és egy másik véletlen változót  , amelyet
, amelyet  függvényeként definiálunk.
függvényeként definiálunk.
Fejezzük ki  az
az  és
és  események indikátorfüggvényeinek segítségével.
események indikátorfüggvényeinek segítségével.
Jelöljük  al az
al az  esemény indikátorát és jelöljük
esemény indikátorát és jelöljük  al az
al az  esemény indikátorát.
esemény indikátorát.  felírhatjuk
felírhatjuk 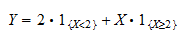
gyakorlat 2
Legyen  pozitív véletlen változó, azaz olyan véletlen változó, amely csak pozitív értékeket vehet fel. Legyen
pozitív véletlen változó, azaz olyan véletlen változó, amely csak pozitív értékeket vehet fel. Legyen  egy konstans. Bizonyítsuk be, hogy
egy konstans. Bizonyítsuk be, hogy  ahol
ahol  a
a  esemény mutatója.
esemény mutatója.
Először is jegyezzük meg, hogy a  és
és  mutatók összege mindig egyenlő
mutatók összege mindig egyenlő  :
: Ezek következtében leírhatjuk
Ezek következtében leírhatjuk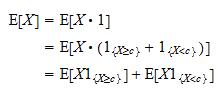 Most jegyezzük meg, hogy
Most jegyezzük meg, hogy  pozitív véletlen változó, és hogy egy pozitív véletlen változó várható értéke pozitív:
pozitív véletlen változó, és hogy egy pozitív véletlen változó várható értéke pozitív: Ezért,
Ezért,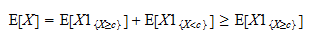
3. gyakorlat
Legyen  egy esemény, és jelöljük a mutatófüggvényét
egy esemény, és jelöljük a mutatófüggvényét  -vel. Legyen
-vel. Legyen  a
a  komplementje és jelöljük indikátorfüggvényét
komplementje és jelöljük indikátorfüggvényét  . Ki tudja-e fejezni
. Ki tudja-e fejezni  a
a  függvényeként?
függvényeként?
A két mutató összege mindig egyenlő  :
: Ezért,
Ezért,
How to cite
Please cite as:
Taboga, Marco (2017). “Indikátorfüggvények”, Előadások a valószínűségelméletről és a matematikai statisztikáról, Harmadik kiadás. Kindle Direct Publishing. Online függelék. https://www.statlect.com/fundamentals-of-probability/indicator-functions.