How do we do a Guinier fit?¶
A Guinier-közelítés csak akkor érvényes, ha az exponenciális \(\exp(-q^2 R_g^2 /3)\)kicsi. Ez azt jelenti, hogy ahhoz, hogy jó Guinier-illesztést végezzünk, eléggé kicsinek kell lennieqRg-nek. Az a qRg-érték, amelynél a Guinier-közelítés egy adott szórásprofil esetében hibásan kezd működni, a szóró általános alakjától függ. Az alábbi ábrán látható a Guinier-közelítés (fekete), valamint a szórásintenzitás egy gömb, egy vékony rúd és egy vékony korong esetében (mindegyik azonos Rg értékkel).
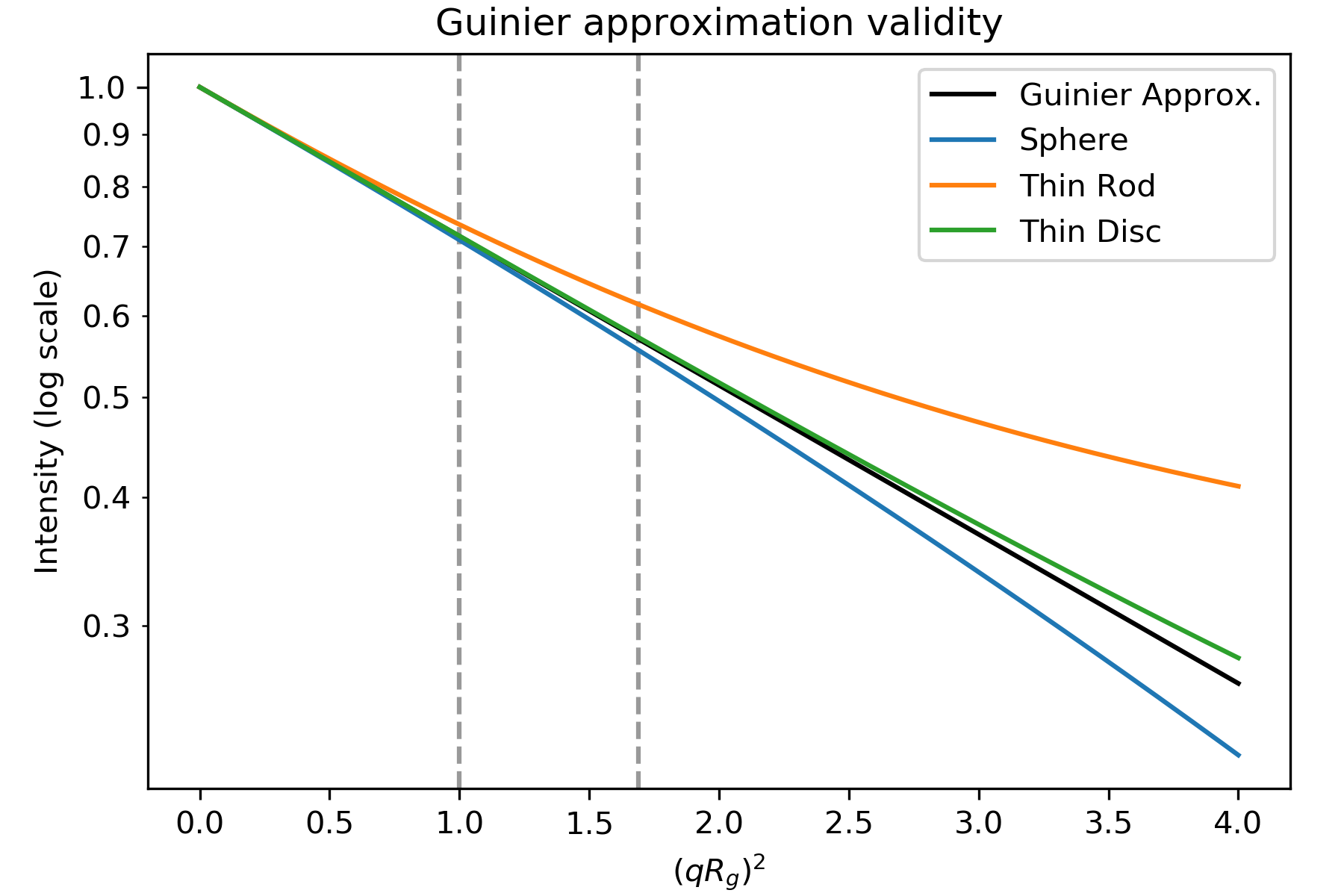
A diagram a 3.3. ábrán alapul. Intenzitás a 3.4. táblázatban szereplő geometriai alakzatokhoz. A szaggatott vonalak 1,0 és 1,3 qRg-nél((qRg) 2 1,0 és 1,69).
Mint látható, a rúd szórási intenzitása csak \(qR_g\sim 1,0\), a gömb \(qR_g\sim 1,3\), a korong pedig \(qR_g\sim 1,7\)-ig egyezik aGuinier közelítéssel. Így az általános részecskeformától függően különböző mennyiségű alacsony q-s adatot kell illesztenie ahhoz, hogy jó Guinier-illesztést kapjon. (Megjegyzés:a grafikon x tengelye (qRg) 2, így \(qR_g\sim 1.3\) 1.69-nél szaggatott vonalként jelenik meg)
A gyakorlatban \(qR_g\sim 1.3\)-ig illesztjük a gömb alakú (gömb- és korongszerű) objektumokat, míg \(qR_g\sim 1.0\)-ig a nagy kiterjedésű (rúdszerű) objektumokat. Ezeket az értékeket úgy választottuk meg, hogy <10%-os hibát eredményezzen a tényleges alak eltérése a Guinier-közelítéstől.Azért fogadjuk el ezt a nagy eltérést, mert az adatok kevesebb pontjának illesztése is bizonytalanságot eredményez, így kompromisszumot kell kötni aközött, hogy mennyire jól működik a közelítés (kisebb maximális qRg-re való illesztés) és mennyire jól lehet illeszteni az adatokat (nagyobb maximális qRg-re való illesztés).
A Guinier-illesztés tartománya így ideális esetben a legkorábbi elérhető qértéktől az 1,0 vagy 1,3 maximális qRg értékig terjed. Tekintettel azonban arra, hogy az Rg a Guinier-illesztésből származik, hogyan határozza meg a helyes maximális q-értéket az illesztés végére? A válasz az, hogy a Guinier-illesztés iteratív módon történik:
- Kitalál egy kezdő maximális q-értéket az illesztéshez.
- Kiszámítja a Guinier-illesztést és megkapja Rg.
- Ha qmaxRg > 1,3 (vagy 1,0), csökkentse a maximális q-t. HaqmaxRg < 1,3 (vagy 1,0), növelje a maximális q-t.
- Ismételje meg a 2. és 3. lépést, amíg a végső maximális q-hoz nem konvergál.
A legtöbb szoftver manapság elvégzi ezt az iteratív keresést Ön helyett, és jó minőségű adatok esetén egy ésszerű maximális q-értéket fog adni, amely esetleg csak egy kis kézi finomítást igényel.
A Guinier-illesztés minimális q-értékét általában az adatokban elérhető legkisebb q-érték határozza meg, amelyet az a műszer állít be, amellyel a mérést végzi.Fontos azonban, hogy a minimális q elég kicsi legyen ahhoz, hogy a Guinier-illesztésnek ésszerű tartománya legyen. Általában a minimális qRg értéknek \(qR_g\leq 0.65\) kell lennie, bár gömb alakú rendszerek esetében az is jó lehet, ha \(qR_g\leq 1.0\). Ez azt jelenti, hogy a minimálisan szükséges q-érték a mért rendszer méretétől függ. Bizonyos esetekben, különösen nagy rendszerek esetén előfordulhat, hogy szándékosan olyan műszert kell keresni, amely kellően alacsony q értékig képes mérni.
Ha adatainknak alacsony q értéknél minőségi problémái vannak, amelyeket a fent felsorolt problémák okozhatnak, úgy találhatjuk, hogy ezen adatok kizárása az illesztésből javíthatja az illesztés minőségét. Bár ez elfogadható lehet, óvatosan kell eljárni, és mindig a teljes adattartományt kell megjeleníteni az ábrákon.A legelfogadhatóbb eset az, amikor az első néhány pont vagy túl magas vagy túl alacsony, de a tartomány többi része tökéletesen illeszkedik (lásd alább a jó illesztés kritériumait). Ebben az esetben a sugárcsúcshoz legközelebb eső néhány pont gyenge statisztikával vagy nagyobb műszeres háttérszórással rendelkezhet, és általában biztonsággal figyelmen kívül hagyható.