A folytonos mintatérben zajló véletlen események legalább két okból hívhatják elő a geometriai képzeteket: a probléma természete vagy a megoldás természete miatt.

Egyes problémák, mint Buffon tűje, a Madarak a dróton, a Bertrand-paradoxon vagy a három darabra tört bot problémája természetüknél fogva geometriai környezetben merülnek fel. Ez utóbbi többszörös átfogalmazást is megenged, amely geometriai alakzatok területeinek összehasonlítását igényli. Általánosságban a geometriai valószínűségekre úgy gondolhatunk, mint nemnegatív (1-nél nem nagyobb) mennyiségekre, amelyeket egy adott tartomány részterületeihez rendelünk bizonyos szabályok szerint. Ha a μ függvény ennek a hozzárendelésnek egy D tartományon definiált kifejezése, akkor például azt követeljük meg, hogy

0 ≤ μ(A) ≤ 1, A ⊂ D és
μ(D) = 1

A μ függvény általában nem minden A ⊂ D-re definiált. D azon részhalmazai, amelyekre μ definiált, azok a véletlen események, amelyek egy adott mintateret alkotnak. Nagyon gyakran μ-et a területek arányával definiáljuk, így ha σ(A) az A halmaz “területeként” definiáljuk, akkor μ(A) = σ(A) / σ(D).

1. probléma

Két barát, akik ugyanarról az állomásról metróval járnak a munkahelyükre, reggel 7 és 7:20 között egyenletesen véletlenszerűen érkeznek az állomásra. Hajlandóak 5 percet várni egymásra, majd felszállnak a vonatra, akár együtt, akár egyedül. Mekkora a valószínűsége annak, hogy az állomáson találkoznak?

Egy (s, t) kartéziánus koordinátarendszerben egy 20 (perc) oldalú négyzet ábrázolja a két barát reggeli metróállomásra érkezésének összes lehetőségét.

A szürke A területet két egyenes, t = s + 5 és t = s – 5 határolja, így A-n belül |s – t| ≤ 5. Ebből következik, hogy a két barát csak akkor fog találkozni, ha s és t érkezésük az A területre esik. Ennek valószínűségét az A területének és a négyzet területének hányadosa adja:

/ 400 = 175/400 = 7/16.

2. feladat

(.)

Három A, B, C pontot véletlenszerűen elhelyezünk egy 1 sugarú körön. Mekkora a valószínűsége annak, hogy ΔABC hegyes?”

Fixáljuk a C pontot. A és B pontok helyzetét ekkor a C pontból két irányban kinyúló α és β ívek határozzák meg. A priori tudjuk, hogy 0 < α + β < 2π. A problémánk szempontjából kedvező α és β értékek (mint lefelé mutató hegyesszögek megfelelnek) 0 < α < π és 0 < β < π. Ezek összege nem lehet kisebb, mint π, mert akkor a C szög tompa lenne, tehát α + β > π. A helyzetet a következő ábra mutatja be, ahol a négyzet oldala 2π.

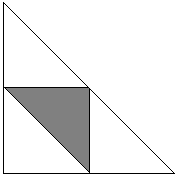
A D régió három félsík metszéspontja: 0 < α, 0 < β és α + β < 2π. Ez a nagy háromszög a fenti ábrán. A kedvező események az árnyékolt háromszögbe tartoznak, amely az α < π, β < π és α + β > π félsíkok metszéspontja. A két félsík területének hányadosa nyilvánvalóan 1/4.

Megjegyezzük most, hogy ha a véletlen háromszög nem hegyes, akkor tompának gondolhatjuk, hiszen annak a valószínűsége, hogy a három pont közül kettő, A, B, C átmérőt alkot, 0. (Ahhoz, hogy BC átmérő legyen, α + β = π-nek kellene lennie, ami egy egyenes, amelynek a területének egyetlen lehetséges hozzárendelése nulla.) Így azt mondhatjuk, hogy annak a valószínűsége, hogy ΔABC tompa, 3/4. Egy tompa háromszög esetén a kör két felére osztható úgy, hogy a háromszög teljes egészében az egyik felén fekszik. Ebből következik, hogy 3/4 a válasz a következő kérdésre:

Három A, B, C pontot véletlenszerűen elhelyezünk egy 1 sugarú körön. Mekkora a valószínűsége annak, hogy mindhárom félkörben fekszik?

1. E. J. Barbeau, Murray S. Klamkin, W. O. J. Moser, Ötszáz matematikai feladat (MAA, 1995, 244. feladat.)
2. D. A. Klain, G.-C. Rota Introduction to Geometric Probability , Cambridge University Press, 1997
3. A. A. Sveshnikov, Problems in Probability Theory, Mathematical Statistics and Theory of Random Functions, Dover, 1978
4. A. M. Yaglom, I. M. Yaglom, Challenging Mathematical Problems With Elementary Solutions, Dover, 1987

Geometriai valószínűség

• Geometriai valószínűségek
• Are Most Triangles Obtuse?
  • Nyolc kiválasztás hat szekcióban
  • Három véletlen pont egy körön
• Geometriai valószínűség
  • Három darabra tört bot (háromvonalas koordináták)
  • Három darabra tört bot. Megoldás kartéziánus koordinátákban
• Bertrand-paradoxon
• Madarak a dróton (feladat és interaktív szimuláció)
  • Madarak a dróton: Megoldás: Nathan Bowler
  • Madarak a dróton. Megoldás: Mark Huber
  • Madarak a dróton: valószínűségi szimuláció. Moshe Eliner
  • Madarak a dróton megoldása. Megoldás: Stuart Anderson
  • Madarak a dróton. Bogdan Lataianu megoldása
• Buffon tésztaszimulációja
• Az esőcseppek átlagolása – egy gyakorlat a geometriai valószínűségszámításból
  • Az esőcseppek átlagolása, 2. rész
• Téglalap a sakktáblán: Bevezetés
• Pálcák jelölése és törése
• Véletlen pontok egy szakaszon
• félkör lefedése
• félgömb lefedése
• Véletlen intervallumok átfedése
• Véletlen intervallumok átfedése
• Véletlen intervallumok. Egy domináns
• Pontok egy négyzetrácson
• Lapos valószínűségek egy gömbön
• Valószínűség háromszögben

|Kapcsolat|||Front page|||Intartalom||Felfelé|

Copyright © 1996-2018 Alexander Bogomolny