Az elektromos töltésről és térről szinte mindent tudunk, de mi a helyzet a Gauss-törvénnyel ? A Gauss-törvény egy fontos téma ebben a fejezetben, de mielőtt rátérnénk a Gauss-törvényre, meg kell értenünk, mi az a Gauss-felület és hogyan határozzuk meg a Gauss-felületet?
Mielőtt továbbmennénk a Gauss-felület meghatározásának módjáról, először is értsük meg, mi az a Gauss-felület.

Mi a Gauss-felület?

Az a felület, amelyen az elektromos tér (E) és a területvektor (A) közötti szög (ө) mindig állandó minden egyes pontban, az ilyen felületet Gauss-felületnek nevezzük.
Meglehet, hogy nem értette az elektromos tér vagy a területvektor fogalmát. Tehát az elektromos mező megismeréséhez van egy külön cikkem az elektromos töltésről és a mezőről, úgyhogy olvasd el te is.
Tudjuk, hogy a vektormennyiségnek van nagysága és iránya, ezért a területvektorok a síkfelület vektorai, amelyek nagysága a felület területe, iránya pedig a felületre merőleges.

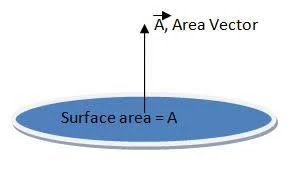
területi vektor

Hát hogyan fogod azonosítani a Gauss-felületet, ha látod?

Hogyan határozzuk meg a Gauss-felületet?

Tudjuk, hogy a Gauss-felület a Gauss-törvényt követi, és az elektromos tér (E) és a területvektor (A) közötti szög (ө) mindig azonos minden pontban. Tehát a Gauss-felület meghatározásához csak azt kell ellenőriznünk, hogy a felület minden egyes pontján a szög (ө) azonos-e vagy sem.
Gauss-törvény:

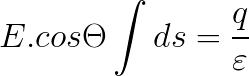
Itt vannak a Gauss-féle felület meghatározásának lépései:
1. lépés: Válasszuk ki a felületet egy testből vagy tárgyból
Az emberek gyakran összezavarodnak, és elkezdik ellenőrizni, hogy egy test minden pontján azonos-e a szög vagy sem. Nos, amit tisztázni kell, az az, hogy azt akarjuk azonosítani, hogy egy test felülete Gauss-felület-e vagy sem, és ezért a szöget (ө) a felület minden egyes pontján, és nem az egész test minden egyes pontján ellenőrizzük.

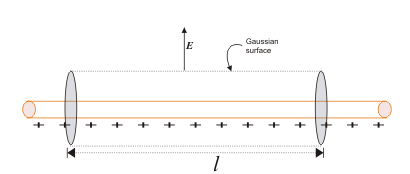
A felület azonosítása

A fenti képen a nem árnyékos területet vesszük figyelembe annak megállapításához, hogy az egy Gauss-felület-e vagy sem, és az árnyékos területet nem vesszük figyelembe, mert azt kell megállapítanunk, hogy egy tárgyon lévő felület Gauss-felület-e vagy sem.
P.s: Ez azt jelenti, hogy egy testnek 1-nél több Gauss-felülete is lehet.
2. lépés: Az elektromos mező irányának ellenőrzése (E)
Most a felület eldöntése után meg kell vizsgálni az elektromos mező irányát a felületről.
Honnan indulnak ki az elektromos mező vonalak a felületen.

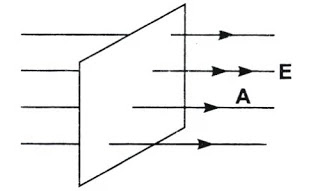
Az elektromos tér iránya

Ha nem tudsz az elektromos térről vagy az elektromos térvonalakról, akkor van egy másik cikkünk is erről, azt is olvasd el, mert kézzel írt jegyzeteket is adtunk az elektromos tér és a Gauss-féle felület és törvény minden egyes levezetéséhez. Kattints ide, hogy elolvasd ezt a cikket
3. lépés: A területvektor (A)
Az elektromos mező irányának ellenőrzése után a felület területvektorát kell ellenőrizned. A területvektor tulajdonképpen egy vektor, amelynek iránya mindig merőleges a felületre.
4. lépés: A területvektor (A) és az elektromos mező (E)
Az elektromos mező és a területvektor irányának meghatározása után itt az ideje, hogy kiderítsük a köztük lévő szöget (ө).

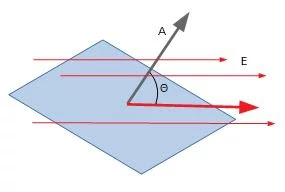
A területvektor és az elektromos tér közötti szög

Vizsgáljuk meg, hogy a kettő közötti szög minden ponton azonos-e. Ha igen! akkor ez egy Gauss-felület.

Nos, egy kérdés merülhet fel benned, hogy miért van szükség a Gauss-felület meghatározására, miért olyan fontos ez?

Miért van szükség a Gauss-felület meghatározására, és hogyan segít ez nekünk?

A Gauss-felület segít nekünk a különböző töltéseloszlás miatti elektromos tér kiértékelésében.
Ha szeretnéd megismerni a különböző töltéseloszlás miatti elektromos tér kiértékelését, akkor a személyes jegyzeteimet feltöltöttem erre az oldalra. Kattintson ide a cikkhez a jegyzetek letöltéséhez.

A Gauss-felület néhány példája:

Tehát néhány példa a Gauss-felületre:
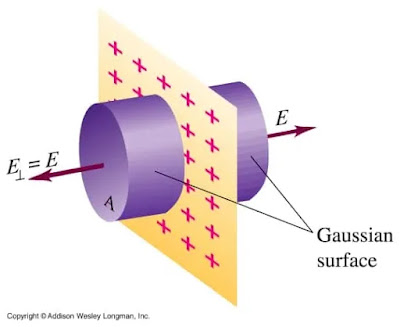
1. Képzeletbeli hengeres Gauss-felület, amelyet egy egyenes töltött vezető okozta elektromos mező megállapítására hoztunk létre. Ezt a levezetést is megtalálod a jegyzeteinkben 🙂

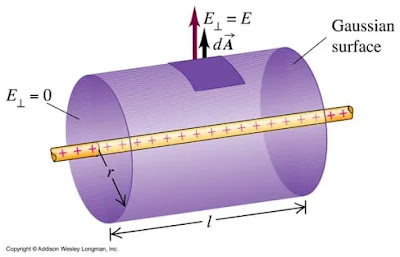
2. Képzeletbeli hengeres Gauss-felület, amelyet sík töltött lap okozta elektromos tér megállapítására hoztunk létre. Ezt a levezetést is megtalálod a jegyzeteinkben 🙂