Statisztikai definíciók > Friedman-teszt
Mi a Friedman-teszt?
A Friedman-teszt egy nem parametrikus teszt a kezelések közötti különbségek megállapítására több kísérlet között. A nemparametrikus azt jelenti, hogy a teszt nem feltételezi, hogy az adatok egy adott eloszlásból származnak (mint például a normális eloszlás). Alapvetően az ANOVA-teszt helyett használják, ha nem ismerjük az adataink eloszlását.
A Friedman-teszt az előjel-teszt kiterjesztése, amelyet több kezelés esetén használunk. Valójában, ha csak két kezelés van, a két teszt azonos.
A teszt lefuttatása
Az adatainak a következő követelményeknek kell megfelelniük:
- Az adatoknak ordinálisnak kell lenniük (pl. Likert-skála) vagy folytonos,
- Az adatok egyetlen csoportból származnak, legalább három különböző alkalommal mérve,
- A minta véletlenszerű mintavételi módszerrel jött létre,
- A blokkok kölcsönösen függetlenek egymástól (ill.azaz minden pár független – egyik nem befolyásolja a másikat),
- A megfigyelések rangsorolva vannak a blokkokon belül, és nincsenek kapcsolatok.
A teszt nullhipotézise az, hogy a kezelések mindegyike azonos hatású, vagy hogy a minták valamilyen módon különböznek. Például eltérő középpontjuk, szórásuk vagy alakjuk van. Az alternatív hipotézis az, hogy a kezeléseknek valóban különböző hatásai vannak.
Készítsük elő az adatokat a teszthez.
1. lépés: Rendezzük az adatokat blokkokba (táblázatkezelő táblázat oszlopaiba).ebben a példában 12 betegünk három különböző kezelést kap.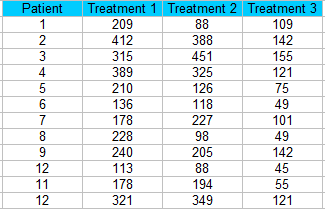
2. lépés: Rendezzük az egyes oszlopokat külön-külön. A legkisebb pontszámnak 1-es rangot kell kapnia. Itt sorokon átívelő rangsorolást végzek, tehát minden egyes beteg minden egyes kezelésnél 1-es, 2-es vagy 3-as rangot kap.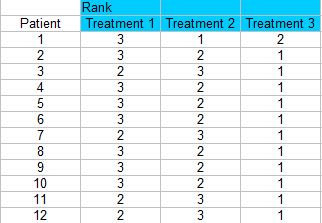
3. lépés: Adjuk össze a rangokat (találjuk meg az egyes oszlopok összegét).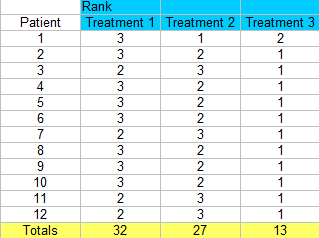
Teszt lefuttatása
Megjegyzés: Ezt a tesztet általában nem kézzel végzik, mivel a számítások idő- és munkaigényesek. Szinte minden népszerű statisztikai szoftvercsomag képes lefuttatni ezt a tesztet. A kézi lépéseket azonban a hivatkozás kedvéért itt is közlöm.
4. lépés: Számítsa ki a tesztstatisztikát. Szükséged lesz:
- n: az alanyok száma (12)
- k: a kezelések száma (3)
- R: a három oszlop összes rangja (32, 27, 13).
Vezessük be ezeket a következő képletbe, és oldjuk meg: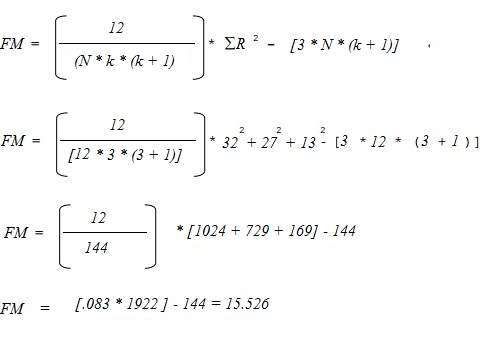
5. lépés: Keressük meg az FM kritikus értéket a Friedman-féle kritikus értékek táblázatából (lásd az alábbi táblázatot).
A k=3 táblázatot használjuk (mivel ennyi kezelésünk van) és 5%-os alfa-szintet. Választhat magasabb vagy alacsonyabb alfa-szintet is, de az 5% meglehetősen gyakori – ezért használja az 5%-os táblázatot, ha nem tudja az alfa-szintet.
A táblázatban az n-12-t keresve 6,17 FM kritikus értéket találunk.
6. lépés: Hasonlítsa össze a kiszámított FM tesztstatisztikát (4. lépés) az FM kritikus értékkel (5. lépés). Utasítsa el a nullhipotézist, ha a számított F-érték nagyobb, mint az FM kritikus érték.:
- Kiszámított FM tesztstatisztika = 15,526.
- FM kritikus érték a táblázatból = 6,17.
A számított FM-statisztika nagyobb, tehát elutasítaná a nullhipotézist.
Friedman’s ANOVA by Ranks Critical Value Table
Három táblázat “k” szerint.
Ha a k értéke 5-nél nagyobb, vagy az n értéke 13-nál nagyobb, akkor az 5. lépésben található Chi-négyzet kritikus érték táblázat segítségével kapja meg a kritikus értéket.
k=3
| N | α <.10 | α ≤.05 | α <.01 |
| 3 | 6.00 | 6.00 | – |
| 4 | 6.00 | 6.50 | 8.00 |
| 5 | 5.20 | 6.40 | 8.40 |
| 6 | 5.33 | 7.00 | 9.00 |
| 7 | 5.43 | 7.14 | 8.86 |
| 8 | 5.25 | 6.25 | 9.00 |
| 9 | 5.56 | 6.22 | 8.67 |
| 10 | 5.00 | 6.20 | 9.60 |
| 11 | 4.91 | 6.54 | 8.91 |
| 12 | 5.17 | 6.17 | 8.67 |
| 13 | 4.77 | 6.00 | 9.39 |
| ∞ | 4.61 | 5.99 | 9.21 |
k=4
| N | α <.10 | α ≤.05 | α <.01 |
| 2 | 6.00 | 6.00 | – |
| 3 | 6.60 | 7.40 | 8.60 |
| 4 | 6.30 | 7.80 | 9.60 |
| 5 | 6.36 | 7.80 | 9.96 |
| 6 | 6.40 | 7.60 | 10.00 |
| 7 | 6.26 | 7.80 | 10.37 |
| 8 | 6.30 | 7.50 | 10.35 |
| ∞ | 6.25 | 7.82 | 11.34 |
k=4
| N | α <.10 | α ≤.05 | α <.01 |
| 3 | 7.47 | 8.53 | 10.13 | 4 | 7.60 | 8.80 | 11.00 | 5 | 7.68 | 8.96 | 11.52 | ∞ | 7.78 | 9.49 | 13.28 |
Hivatkozás:
Friedman’s Two-way Analysis of Variance by Ranks – Analysis of k-Within-Group Data with a
Quantitative Response Variable. Retrieved 7-17-2016 from: http://psych.unl.edu/psycrs/handcomp/hcfried.PDF
Stephanie Glen. “Friedman’s Test / Two Way Analysis of Variance by Ranks” From StatisticsHowTo.com: Elementary Statistics for the rest of us! https://www.statisticshowto.com/friedmans-test/
——————————————————————————
Segítségre van szüksége egy házi feladathoz vagy tesztkérdéshez? A Chegg Study segítségével lépésről lépésre megoldásokat kaphat kérdéseire a terület szakértőjétől. Az első 30 perc egy Chegg oktatóval ingyenes!