Hogyan számítsuk ki a tárgyat felfüggesztő kötelek feszültségét

Az alábbi ábrán láthatjuk, hogy a tárgy felemeléséhez szükséges erő, F, megegyezik a tárgy súlyával, W-vel. Ez a gondolat az az alapvető fogalom, amely a feszítőerő képletünk alapjául szolgál. Szintén az alábbiakban látható a tárgy szabadtest-diagramja, amely a húrban ható T feszültségerőket mutatja. Mint látható, a feszítőerők párban és ellentétes irányban jelentkeznek:

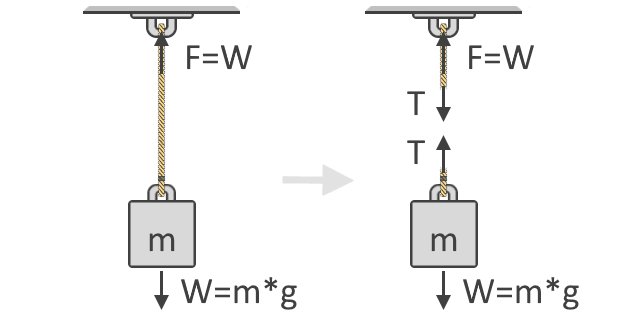
A Newton második mozgástörvényét követve ezután az erők összegzését a tárgy szabadtest-diagramja segítségével fejezhetjük ki, ahogy a fenti ábra jobb oldalán látható. A szabadtest-diagramokat arra használjuk, hogy megmutassuk a testre ható erők különböző irányait és nagyságát. Egyensúlyban ezeknek az erőknek mind nullának kell lenniük. Ha minden felfelé ható erőt pozitívnak, lefelé ható erőt pedig negatívnak tekintünk, akkor az egyenletünk:

ΣF = 0 = T + (-W)
T = W
ahol a súly, W, negatív lesz, mivel lefelé irányul. A W-t az egyenlet másik oldalára átültetve most már láthatjuk, hogy a kötélben lévő feszítőerő egyenlő a rajta lévő tárgy súlyával, ahogyan az fentebb is látható.

Ha több kötelet használunk a tárgy felemeléséhez, akkor a teljes feszítőerő feleződik a kötelek között. Az egyes kötelekben lévő feszítőerő függ azok szögétől a velük szemben álló erő irányához képest. Ennek további megértéséhez tekintsünk egy másik szabadtest-diagramot egy két kötéllel felfüggesztett tárgyról, az alábbiak szerint:

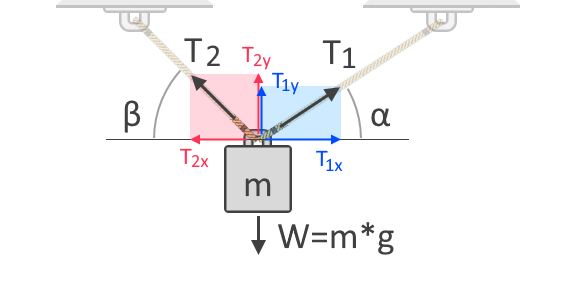
A fenti szabadtest-diagramon láthatjuk a feszítőerők T₁, illetve T₂ vízszintes és függőleges komponenseit. Az erők vektorok, ami azt jelenti, hogy mindig van nagyságuk és irányuk is. Mint minden vektor, az erők is kifejezhetők ezekben a komponensekben, amelyek megadják az erő hatását a vízszintes és függőleges tengely mentén. T₁ₓ és T₂ₓ a T₁ és T₂ függőleges komponensei. Másrészt T₁ᵧ és T₂ᵧ ugyanezen erők függőleges komponensei. Mivel a gravitáció a függőleges tengelyen hat a tárgyra, az erők összegzéséhez a következőképpen kell figyelembe vennünk a feszítőerők függőleges komponenseit:

ΣF = 0 = T₁ᵧ + T₂ᵧ + (-W)
W = T₁ᵧ + T₂ᵧ

Mivel a feszítőerők szögeit is ismerjük, a T₁ᵧ és T₂ᵧ értékeket a T₁, illetve T₂ függvények segítségével trigonometrikus függvények segítségével tudjuk kifejezni:

T₁ᵧ = T₁ * sin(α)
T₂ᵧ = T₂ * sin(β)
W = T₁ * sin(α) + T₂ * sin(β)

Mondhatjuk azt is, hogy ahhoz, hogy a rendszer egyensúlyban legyen, a tárgy nem mozoghat vízszintesen vagy az x tengely mentén. Ezért a T₁ és a T₂ vízszintes összetevőinek ekkor nullának kell lennie. Emellett a trigonometria segítségével a T₁ₓ és a T₂ₓ-t a T₁ és a T₂ függvényében is ki tudjuk fejezni:

T₁ₓ = T₂ₓ
T₁ * cos(α) = T₂ * cos(β)

Ha mindkét oldalt elosztjuk cos(α)-tal, akkor olyan egyenletet kapunk, amelyben a T₁-t a T₂ és a szögek függvényében fejezzük ki:

T₁ = T₂ * cos(β) / cos(α)

Majd ezt az egyenletet használhatjuk a T₂ megoldására, ha T₂ * cos(β) / cos(α)-t T₁-ként helyettesítjük az erők összegző egyenletében, az alábbiak szerint:

W = T₁ * sin(α) + T₂ * sin(β)
W = T₂ * * sin(α) + T₂ * sin(β)
W = T₂ *
T₂ = W /

Végül, ha ezt az egész egyenletet megszorozzuk cos(β) / cos(α)-el, ahogyan a T₁ értékét a T₂ értékében levezettük, majd mindent egyszerűsítve ezt az egyenletet kapjuk:

T₁ = W / *
T₁ = W / *
T₁ = W /

Most már csak a feszítőkötelek vízszinteshez viszonyított szögeit kell tudnunk. Ha megadunk egy szöget a függőlegeshez képest, akkor csak vonjuk ki ezt a szöget a 90°-ból. Így megkapod a vízszinteshez viszonyított szöget. Ha azonban más szögértékeket adnak meg, amelyek nagyobbak lehetnek 90°-nál vagy akár 180°-nál, akkor érdemes megnézni referencia-szögszámológépünket, amely segít meghatározni a szükséges szöget. Miután meghatároztuk a változók értékeit a feszítőerő képleteinkben, most már meg tudjuk oldani a feszítőerőket.