Mennyit tudsz a végtelenekről? Valószínűleg hallottál már olyan számról, amely a lehető legnagyobb szám, vagy lehetetlenül nagy.

A végtelen számok magyarázatához először néhány fogalmat kell definiálnom.

A végtelen számok számolásra használt számok. Az egész számok halmazát úgy definiáljuk, mint az összes olyan számot, amelynek nincs tört összetevője. Néhány példa:

A végtelen a természetes számok határain túli objektum fogalma. Először egy Georg Cantor nevű orosz matematikus fogalmazta meg, aki nemcsak bevezette a végtelenséget, hanem azt is kimutatta, hogy többféle végtelen létezik.

Cantor ellentmondásos bizonyítást adott a végtelenségekről, amely szerint egyes végtelenek nagyobbak, mint mások. Ez elsőre lehetetlennek tűnhet – hogyan lehet egy tárgy nagyobb egy másik tárgynál, amely végtelen?

Cantor a matematika egy látszólag használhatatlan ágára alapozta bizonyítását: A halmazelmélet. A halmaz objektumok gyűjteménye – például lehet olyan halmazunk, amely tartalmazza az 1-et, a 2-őt és a 3-at. Ezeket a halmazban lévő objektumokat elemeknek nevezzük.

Matematikai jelöléssel ez így nézne ki:

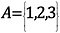
A halmaz elemeinek száma, vagyis a halmaz kardinalitása 3.

Ezt így jelöljük:

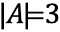
Ha most van egy másik halmazunk, B, amely tárgyakat tartalmaz, úgy, hogy

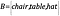
Honnan tudjuk, hogy a halmazok azonos méretűek?

Egyik módja ennek, hogy megszámoljuk a második halmaz elemeinek számát. Jól látjuk, hogy ebben a halmazban is 3 elem van, így tudjuk, hogy a két halmaz mérete megegyezik.

Egy másik módszer, hogy a második halmazunkat, a B-t, leképezéssel összehasonlítjuk az első halmazunkkal, az A-val.

Az A halmaz első elemét , az 1-et, leképezhetjük a B halmaz első elemére, a székre.

A második elemet az A halmazból, 2, leképezhetjük a B halmaz második elemére, az asztalra.

A harmadik elemet az A halmazból, 3, leképezhetjük a B halmaz harmadik elemére, a kalapra.

Mivel az A halmaz minden elemét pontosan 1 elemre képezzük le a B halmazból, a halmazok egyenlő méretűek.

Most nézzük meg a végtelen halmazokat. Az elején említett egész számok halmaza végtelen halmaz – végtelen sok egész szám van. Az egész számok halmazát a

jelöli a páros számok halmazát, amelyet jelölhetünk

az alábbiak szerint definiált

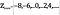
Intuitívan, úgy tűnhet, hogy

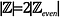
mert minden páros egész számra 2 egész szám jut: 1 páratlan egész szám és 1 páros egész szám. Ellenőrizzük ezt.

Próbáljuk meg összehasonlítani a halmazokat úgy, hogy elemeket képezünk le az 1 halmazból a másikba.

Az 1-t leképezhetjük a 2-re, a 2-t a 4-re, a 3-at a 6-ra, és így tovább.

Ha ez így megy végig a halmazokon, akkor láthatjuk, hogy az egész számú halmaz minden eleme pontosan 1 elemet képez le a páros egész számú halmazból.

Így, bár ellentmondásosnak tűnhet, a halmazok mérete megegyezik.

Hogy a halmazok mérete megegyezik.