A TensorFlow kódot ezen a linken (vagy egy PyTorch verziót ezen a linken) futtathatod magad, vagy tovább olvashatod, hogy megnézd a kódot futtatás nélkül. Mivel a kód kicsit hosszabb, mint az előző részekben, itt csak a legfontosabb darabokat fogom megmutatni. A teljes forráskód elérhető a fenti linket követve.

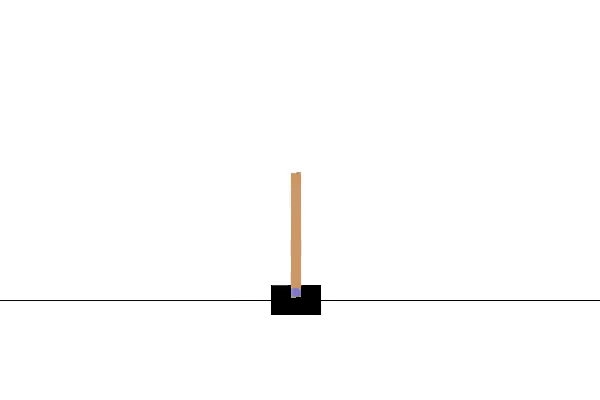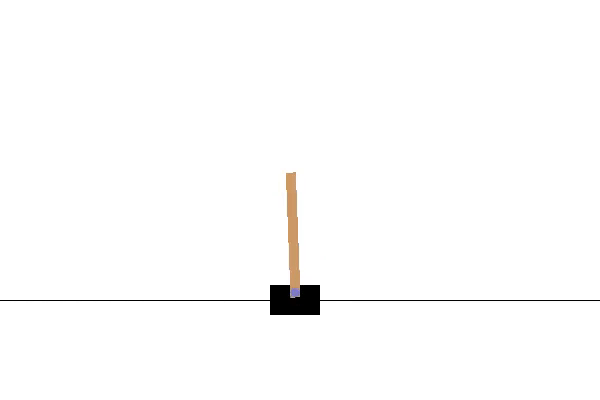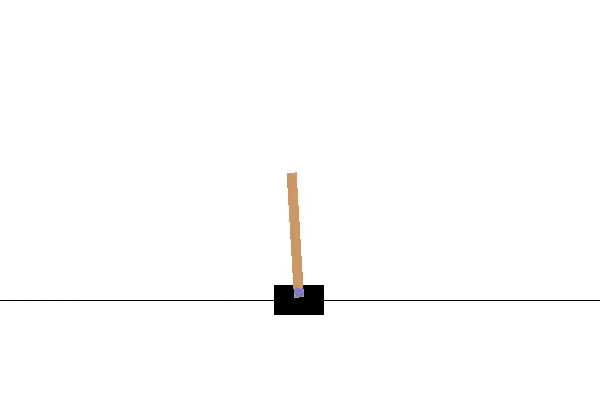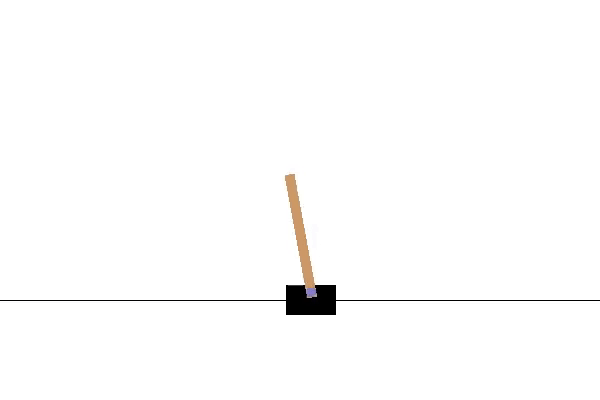
Itt a CartPole környezet. A környezet megjelenítéséhez és futtatásához az OpenAI Gym-et használom. A cél a kocsit jobbra és balra mozgatni, hogy a rúd függőleges helyzetben maradjon. Ha a rúd dőlése 15 foknál nagyobb mértékben eltér a függőleges tengelytől, az epizód véget ér, és kezdjük elölről. Az 1. videó egy példát mutat arra, hogy több epizódot is lefuttathatunk ebben a környezetben, véletlenszerű cselekvésekkel.

A DQN algoritmus megvalósításához először létrehozzuk a fő (main_nn) és a cél (target_nn) DNN-eket. A célhálózat a fő hálózat másolata lesz, de a súlyok saját másolatával. Szükségünk lesz még egy optimalizálóra és egy veszteségfüggvényre.

A következő lépésben létrehozzuk a tapasztalatok visszajátszásának pufferét, hogy a tapasztalatokat hozzáadjuk a pufferhez, és később mintát vegyünk belőlük a képzéshez.

Egy segédfüggvényt is írunk az ε-greedy politika futtatásához, és a pufferben tárolt adatok felhasználásával a fő hálózat betanításához.

Meghatározzuk a szükséges hiperparamétereket is, és betanítjuk a neurális hálózatot. Lejátszunk egy epizódot az ε-greedy politikával, az adatokat a tapasztalatok visszajátszásának pufferében tároljuk, és minden lépés után betanítjuk a főhálót. Minden 2000 lépés után egyszer átmásoljuk a súlyokat a fő hálózatból a célhálózatba. Az epsilon (ε) értékét is csökkenteni fogjuk, hogy magas feltárással kezdjünk, és idővel csökkentsük a feltárást. Látni fogjuk, hogy az algoritmus minden egyes epizód után hogyan kezd el tanulni.

Ez lesz a megjelenő eredmény:

Episode 0/1000. Epsilon: 0.99. Reward in last 100 episodes: 14.0 Episode 50/1000. Epsilon: 0.94. Reward in last 100 episodes: 22.2 Episode 100/1000. Epsilon: 0.89. Reward in last 100 episodes: 23.3 Episode 150/1000. Epsilon: 0.84. Reward in last 100 episodes: 23.4 Episode 200/1000. Epsilon: 0.79. Reward in last 100 episodes: 24.9 Episode 250/1000. Epsilon: 0.74. Reward in last 100 episodes: 30.4 Episode 300/1000. Epsilon: 0.69. Reward in last 100 episodes: 38.4 Episode 350/1000. Epsilon: 0.64. Reward in last 100 episodes: 51.4 Episode 400/1000. Epsilon: 0.59. Reward in last 100 episodes: 68.2 Episode 450/1000. Epsilon: 0.54. Reward in last 100 episodes: 82.4 Episode 500/1000. Epsilon: 0.49. Reward in last 100 episodes: 102.1 Episode 550/1000. Epsilon: 0.44. Reward in last 100 episodes: 129.7 Episode 600/1000. Epsilon: 0.39. Reward in last 100 episodes: 151.7 Episode 650/1000. Epsilon: 0.34. Reward in last 100 episodes: 173.0 Episode 700/1000. Epsilon: 0.29. Reward in last 100 episodes: 187.3 Episode 750/1000. Epsilon: 0.24. Reward in last 100 episodes: 190.9 Episode 800/1000. Epsilon: 0.19. Reward in last 100 episodes: 194.6 Episode 850/1000. Epsilon: 0.14. Reward in last 100 episodes: 195.9 Episode 900/1000. Epsilon: 0.09. Reward in last 100 episodes: 197.9 Episode 950/1000. Epsilon: 0.05. Reward in last 100 episodes: 200.0 Episode 1000/1000. Epsilon: 0.05. Reward in last 100 episodes: 200.0

Most, hogy az ágens megtanulta maximalizálni a CartPole környezet jutalmát, még egyszer interakcióba hozzuk az ágenst a környezettel, hogy megjelenítsük az eredményt, és lássuk, hogy most már 200 képkockán keresztül képes egyensúlyban tartani a pólust.

A TensorFlow kódot ezen a linken (vagy a PyTorch változatot ezen a linken) saját maga is futtathatja.