Az Ising-modell a termodinamikai rendszer egy különleges példája, és ez a modellrendszer a fázisátmenetek megértéséhez. Tudod, miért tölt annyi biológus annyi időt vacak gyümölcslegyekkel? Nos, a fizikusok is sok időt töltenek az Ising-modellel. Ahogy Raghu professzor segítőkészen elmondja nekünk, ez a fázisátmenetek Drosophilája.

Személy szerint én nem vagyok a legnagyobb rajongója az analógiájának, mert szerintem a gyümölcslegyek undorítóak. Remélhetőleg az Ising-modell nem lesz túl durva.

Motiváció

Miért kellene ennyi időt töltenünk az Ising-modellről való beszélgetéssel?

• Meglepően hasznos, mert segít elgondolkodni a fázisátmenetekkel kapcsolatos mindenféle viselkedésről. Például:

  • az Ising-modell szimmetriatörést mutat alacsony hőmérsékletű fázisban (amiről az imént beszéltünk)

  • van egy speciális “kritikus pontja” egy jól meghatározott hőmérsékleten (amire utaltunk a víz fázisdiagramjánál)

  • egyéb gazdag tulajdonságai.

• Ez egyike azon kevés pontosan megoldható modelleknek, ahol ténylegesen ki tudjuk számítani a termodinamikai mennyiségeket és értelmezni tudjuk őket.

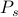  • A termodinamikai mennyiségek kiszámítása általában nehéz, mert sok tételt kell összegeznünk. Emlékezzünk az első termoóránkról, hogy egy egyensúlyi rendszerre úgy is gondolhatunk, mint sok állapot együttesére, amelyek mindegyike a saját valószínűségével van súlyozva. Ebben a keretben a megfigyelt termodinamikai mennyiségek az együttesre vonatkozó átlagoknak felelnek meg. Különösen, ha valamilyen 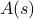megfigyelhető mennyiség együttes átlagát akarjuk megtalálni, akkor meg kell találnunk az összeget 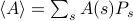, ahol az összeg az összes lehetséges állapoton fut át. A probléma ezzel, mint emlékszel, az, hogy egy termodinamikai rendszer állapotainak száma exponenciálisan skálázódik a részecskék számával! Még egy közepes méretű rendszer esetében is egyszerűen túl sok állapot van ahhoz, hogy egy számítógép explicit módon kiszámítsa az átlagot – nem beszélve egy olyan termodinamikai rendszerről, ahol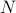 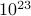nagyságrendű.

  • Az eloszlásfüggvény kiszámításához tehát ”okosnak kell lennünk”, és hálásnak kellene lennünk az pontosan megoldható rendszerekért!

• Az Ising-modell egyszerű, mégis meglepően sok különböző rendszerre alkalmazható.

  • Ez az első ízelítőnk az egyetemességből – a kritikus jelenségek azon tulajdonságából, hogy ugyanaz az elmélet mindenféle különböző fázisátalakulásra alkalmazható, akár folyadékokban és gázokban, akár mágnesekben vagy szupravezetőkben vagy bármi másban. A fizikusok szeretik ezt a fajta általános viselkedést, mert egyfajta mélyebb rendet sugall kaotikus világunkban.

Az Ising-modell definíciója

Az Ising-modell egy matematikai modell, amely nem felel meg egy tényleges fizikai rendszernek. Ez egy hatalmas (négyzet alakú), helyekből álló rács, ahol minden egyes hely két állapot egyikében lehet. Minden egyes helyet indexszel jelölünk, és a két állapotot és -nak nevezzük. Ha azt akarjuk mondani, hogy a ‘s hely a állapotban van, azt írjuk, hogy .

Most, ez a definíció sajnálatosan absztrakt és nem fizikai, ezért nekünk fizikusoknak rendkívül hasznos, ha egy tényleges rendszerre gondolunk, hogy valami explicitre hivatkozhassunk és fizikai intuíciót építhessünk. Íme néhány fizikai rendszer, amelyet az Ising-modell reprezentálhat:

• Egy mágnes. Minden egyes oldal egy adott “spint” képvisel az anyagban (egy párosítatlan elektron??), és ez , ha a spin lefelé mutat, vagy , ha a spin felfelé mutat. Minden egyes spin úgy viselkedik, mint egy mini mágnes a saját mini mágneses momentumával; ha az összes spin egy vonalban van, akkor a spinek egész rácsa úgy viselkedik, mint egy nagy mágnes, nettó makroszkopikus mágneses momentummal.

• Egy ötvözet; mondjuk sárgaréz. Minden egyes hely egy-egy atomot jelent a rácsban; egy rézatomot jelent az adott helyen; a cinket.

• Egy ”rácsgáz”. Minden egyes hely egy részecske lehetséges helyét jelenti; azt jelenti, hogy az adott hely üres, pedig azt, hogy az adott helyet egy részecske foglalja el.

• Bakteriális örvényrácsok???

Előre úgy gondolunk az Ising-modellre, mint egy mágnes modelljére. Ez egy mágnesnek egy durván leegyszerűsített és játékmodellje, az biztos, de a mágnes analógia ennek ellenére segíthet eligazodni dédelgetett fizikai intuíciónkban.

A Hamilton-modell összerakása

A mágnesnek ezzel a Mickey-egér modelljével kapcsolatban természetes kérdés, hogy milyen energiája van. Pontosabban fel akarunk írni egy olyan függvényt, amely a mágnesben lévő spinek minden egyes lehetséges konfigurációjának (más néven mikroállapotának) energiáját reprezentálja. Mint tudjuk, ezt az energiafüggvényt Hamilton-függvénynek nevezzük.

Az Ising-modellben a Hamilton-függvény kétféle kölcsönhatást tartalmaz:

• a külső mezőtermet. Ahogy a kvantummechanikából emlékszünk rá, egy külső mágneses tér képes megosztani a spin-down és spin-up állapot energiáit, úgy, hogy az egyiknek nagyobb az energiája, a másiknak pedig kisebb.

  • A nagysága azt mutatja, hogy milyen erős a mező, tehát azt, hogy az egyik spin energiája mennyivel nagyobb, mint a másiké.

  • A előjele azt mutatja, hogy a spin-up vagy a spin-down állapotot részesíti előnyben.

  • Mivel minden egyes spin érzi a külső mezőt, össze kell összegeznünk az összes helyet, hogy megtaláljuk a teljes hozzájárulást az energiához.

• a szomszédos spinek közötti kölcsönhatási kifejezés – lehet, hogy egymáshoz akarnak igazodni és ugyanoda mutatnak, lehet, hogy ellenigazodni akarnak és különböző irányba mutatnak. Fizikailag elképzelhető, hogy ez a kölcsönhatás azért keletkezik, mert a mágnesben minden egyes spin egy saját mini mágneses dipólus, amely saját mágneses mezőt állít fel, és a szomszédai érzik ezt a mágneses mezőt.

  • A nagysága megmondja, hogy a szomszédos spinek milyen erősen kapcsolódnak egymáshoz – mennyire akarnak (anti)igazodni. Fizikailag a spin-spin csatolás erőssége függhet például a köztük lévő távolságtól a maget rácsban.

  • A előjele megmondja, hogy a szomszédos spinek inkább igazodnak vagy inkább ellenigazodnak. (Ennek szakkifejezése ferromágneses, illetve antiferromágneses). Fizikailag az, hogy egy anyag az egyik vagy a másik (vagy egyik sem), a spinek kölcsönhatásának pontos kvantummechanikai részleteitől függ.

  • Mivel a spin-spin kölcsönhatás két spin között keletkezik, össze kell összegeznünk a helypárokat, hogy megtaláljuk a teljes kölcsönhatás energiáját.

Bővebben a kölcsönhatási kifejezésről

A spin-spin kölcsönhatási kifejezéssel kapcsolatban természetes kérdés, hogy mely spinek milyen spinekkel vannak összekapcsolva?

Ha ismét visszakanyarodunk a mágnes fizikai képéhez, és ráközelítünk egy adott spinre, akkor azt várnánk, hogy a spin-spin kölcsönhatás erőssége a közeli spinek esetében erősebb, a távoli spinek esetében pedig gyengébb. A spin-spin kölcsönhatás pontos távolságfüggése a tényleges mágnesek esetében valószínűleg meglehetősen bonyolult.

Az Ising-modell esetében a lehető legegyszerűbb feltételezést tesszük ennek a spin-spin kölcsönhatásnak a természetére:

Néhány megjegyzés:

• Egy dimenziós négyzetes rácsban minden helynek 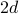legközelebbi szomszédja van: balra és jobbra az egyik dimenzióban, fel és le, ha hozzáadjuk a második dimenziót, stb…

• A kölcsönhatást izotrópnak feltételezzük – minden szomszédot egyformán kezelünk iránytól függetlenül.

• A legközelebbi szomszédos kölcsönhatásokról gyakran úgy beszélünk, mint a két rácshelyet összekötő kötés energiájáról.

• Amikor szomszédos helypárok felett összegzünk, szimbolikusan kis szögletes zárójeleket írunk az indexek köré a ”legközelebbi szomszéd” jelzésére.

A legközelebbi szomszédos kölcsönhatások szép következménye, hogy amikor a spinek valamely konfigurációjának teljes energiáját keressük, az összes lehetséges helypár helyett csak az egymással szomszédos helypárokat összegezzük.

Most, hogy ezeket a dolgokat megbeszéltük, készen állunk arra, hogy leírjuk a Hamiltoniánus tényleges kifejezését. (A Hamiltonián leírása előtt szerettem volna elmagyarázni és értelmezni a fizikát, hogy a szimbólumoknak legyen valami értelme.)

Az Ising-modell Hamiltoniánja

Az Ising-modell Hamiltoniánja a következőképpen írható fel:

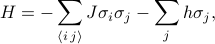
ahol a spin-spin kölcsönhatást jelenti, a külső mezőt, és a 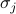az egyes rácshelyeken lévő egyedi spineket. Az első összeg a szomszédos rácshelyek (más néven kötések) összes párjára vonatkozik; a spinek közötti kölcsönhatást jelenti. A második összeg magukra a rácshelyekre vonatkozik; ez jelenti a külső mezőt, amely az összes spint egy irányba próbálja igazítani.

Tovább az Ising-modell termodinamikájához.