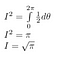Lord Kelvin írt erről az integrálról: “
Öröm az örömben 😉
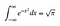
OK, feltételezem, hogy ismered az integrálás és differenciálás alapjait. A következőkben némi intuíciót adunk a későbbiekben következő okos trükkökhöz. Ne aggódj, ha némelyik kissé zavarba ejtő, csak próbálj ráérezni, mi történik.
A stratégia itt az lesz, hogy ügyes helyettesítést végzünk. De mi egy helyettesítést fogunk végezni két változóban. A mostani problémát úgy is elképzelhetjük, mint egy görbe alatti terület kiszámítását
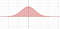
De megmutatjuk, hogy a probléma átfordítható egy térfogatszámítássá.
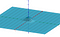
A térfogat kiszámításához egy kicsit más változóváltozási képletet használunk, mint amit a normál integráloknál használunk. Polárkoordinátákat fogunk használni. Ez az x- és y-koordinátákat a sugaruk és a szögük függvényében fejezi ki. A Geogebrának van egy szép interaktív módja ennek megtekintésére itt

Azután a polárkoordináták bűvös bázisváltási képletét fogjuk használni.
A görbe alatti terület kiszámításánál volt a ‘dx’ elem, amely egy kis távolságot jelent az x tengely mentén. A térfogat kiszámításakor van dx dy, ami olyan, mint egy kis téglalap, amelynek oldalhosszúsága dx és dy. Ezeket az alapokat aztán arra használjuk, hogy létrehozzunk egy sor négyzetet, amelyek megbecsülik a térfogatot. Ezt a legkönnyebben az alábbi szemléltetéssel láthatjuk. Az integrál ezeknek a közelítéseknek a határértéke.
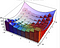
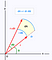
Ha ehelyett a polárkoordináta-rendszert használjuk, akkor egy kissé eltérő területelemet kapunk alatta. Az alábbiakban dA a területelem. A szög és a sugár kis változtatásával ez a területelem egyre jobban közelíthető egy téglalappal, amelynek oldalhossza dr, illetve r*dtheta. Ha jártasak vagyunk némi geometriában, kis theta esetén a sin(theta) nagyon jól közelíthető thetával, és akkor bizonyítani tudjuk az alábbi eredményt.
Az integrál megoldása
Először is adjunk nevet az integrálunknak. Nevezzük I.
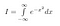
Megjegyezzük, hogy x csak egy “dummy változó”. A terület attól függetlenül létezik, hogy milyen változónevet használunk. Tehát a következő két egyenletet is felírhatjuk
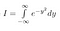
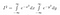
Most, mivel I csak egy állandó, bár annak az értékét még nem tudjuk, használhatjuk a szokásos szabályainkat egy konstans integrálba való bevitelére
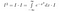
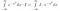
Most nem sok érdemlegeset tettünk. Most erősen elgondolkodunk azon, hogy mit jelent az integrál. Függvények integrálját vesszük. Ha két függvény mindenhol ugyanazt az értéket veszi fel, akkor azonosak, és ugyanolyan területűek. Ezt szem előtt tartva elvégezhetjük a következő manipulációkat, ha az I*exp(-x²) értéket x függvényének tekintjük, vagyis olyasminek, ami bemenetként x értékeket vesz fel, és kimenetként egy számot ad.
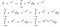
Oké, ez sok volt, amit be kellett fogadnunk. Az első sorban csak átírtuk az I-t integrális formában, más változónévvel. A második sorban az I*exp(-x²) függvényként kezelve rájöttünk, hogy az exp(-x²)-t behozhatjuk a dy integrálba, és ez még mindig ugyanazt a kimeneti értéket adja x bármely bemeneti értékére. Végül felhasználtuk az exponenciálás szabályait.
Az egészet kiírva most
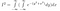
A következő a gyilkos felismerés. Fentebb a változónevekkel és a függvények ábrázolásának módjával babráltunk. Most nézőpontot váltunk: ez a kifejezés is az exp(-(y²+x²)) egész 2D-s síkra vonatkozó integrálját reprezentálja, amelynek területeleme dA = dx dy. Vagyis dx dy egy kis téglalap a síkon, és exp(-(y²+x²)) az e téglalap feletti magasság.
A következőkben használjuk a korábban
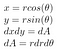
Amint sin² + cos² = 1, miután mindent bedugtunk, megkapjuk
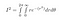
r 0-tól a végtelenig, theta pedig 0-tól 2*pi-ig terjed, mivel ez a teljes 2D-síkot lefedi: bármely pont sugara kisebb, mint a végtelen, és szöge 0 és 2pi radián között van.
A belső integrált a láncszabály
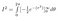
Az ígéret földjén találjuk magunkat: