A nullának számos érdekes tulajdonsága van, ami miatt a matematikusok számára érdekes. Ha bármely számhoz hozzáadjuk vagy kivonjuk a nullát, a szám ugyanaz marad Ha 0-t megszorozzuk bármely számmal, az eredmény 0. Bármely nulladik (0.) hatványra emelt szám 1, tehát 20=1 és 560=1 . A hagyományos algebrában a 0-val való osztás nem definiált, így egyetlen szám sem osztható 0-val. A 0 szám a valós számok és a komplex számok eleme is.

A 0 szám története

Honnan származik a nulla gondolata? Manapság intuitívnak tűnik számunkra; a nulla olyan szám, amely egy nulla mennyiséget jelöl – egy semmit. A társadalomban mindenütt nullákat látunk, és természetesen megértjük, hogy mit jelentenek, és hogyan lehet matematikailag manipulálni őket. Történelmileg azonban a 0 fogalmának a matematika tárgyaként való általános elismerése elég sokáig tartott, és a történelem során sokan azt állították, hogy a nulla szám nem létezik, vagy hogy a nulla fogalma inkoherens fogalom.

Néhány ősi társadalomnak nem volt kifejezett fogalma a nulla mennyiségéről vagy egy konkrét számjegyről, amelyet annak ábrázolására használhattak volna. Az ókori egyiptomiaknak és a babilóniaiaknak is volt valamilyen elképzelésük a nulla mennyiségről, és szükségük volt helyőrző értékekre a számok ábrázolásában, de soha nem fejlesztettek ki külön számjegyet vagy fogalmat e mennyiség vagy helyőrző érték ábrázolására. Az ókori egyiptomi számrendszerek teljesen képszerűek voltak, és nem rendelkeztek helytartó értékekkel, míg az ókori babilóniaiak a számok közötti szóközöket használták a helytartó értékek ábrázolására.

A majáknak volt egy kifejezett fogalma a 0-ról, és volt egy külön számjegyük a fogalom ábrázolására és helytartó értékként való használatára a vigesimal (bázis 20) naptárrendszerükben. Míg a maják, olmékok és más prekolumbián társadalmak a történelemben az elsők között voltak, amelyeknek kifejezett és kifinomult fogalma volt a 0 számról, ezek a rendszerek nem voltak hatással az európai óvilági társadalmakra.

Az ókori görögöknek viszont bonyolult kapcsolatuk volt a nullával. Nem volt szimbólumuk sem a fogalmára, sem a helyőrző értékére, mert nem voltak biztosak abban, hogy a 0 számot valóban létező dolognak lehet-e tekinteni. Hogyan, kérdezték, hogyan lehet valami (egy szám) semmi (nulla)? A görögök számára a természetes számok (1, 2, 3, 4,…) a világ diszkrét egyedi objektumainak megértéséből származtak. Maga Arisztotelész híres érvelése szerint a 0 nem létezik, azzal az indokkal, hogy a 0 ürességet vagy semmit jelent, és valódi üresség vagy semmi nem létezhet.

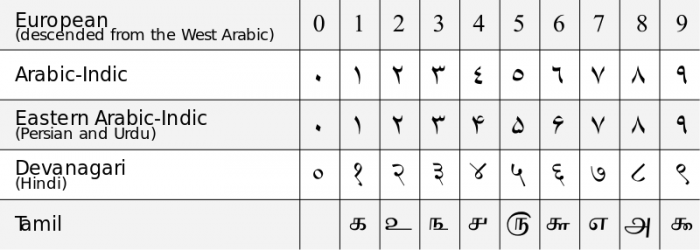
A kínaiak a “0”-t úgy értelmezték, mint egy helyőrző számjegyet a számolási rendszerükben, de a “0”-t nem tekintették úgy, hogy bármilyen különálló számot jelentene, csak egy hasznos szimbólumnak. A 0-nak mint különálló számnak és a helymegjelölési rendszerek számjegyének általános értelmezése Indiából származik a Kr. u. 6. században. Az akkori indiai matematikusok dolgozták ki az első olyan tizedesjegyrendszereket (10-es bázis), amelyek a 0-t különálló számjegyként tartalmazták, és tisztában voltak a nulla egyedi matematikai tulajdonságaival. A Kr. u. 11. századra a nulla gondolata az Omajjád kalifátus alatt Spanyolországban élő iszlám matematikusok hatására Nyugat-Európába is átterjedt, és létrejött a mai arab számrendszer, a tizedesjegyrendszer. Az angol “zero” szó első használata 1589-ből származik.

A nulla matematikai tulajdonságai

A nulla szám szerves szerepet játszik a matematika szinte minden területén. A nulla a legkisebb nemnegatív egész szám, és nem folytatódik vele természetes szám. Mivel a 0 egész szám, ezért racionális szám, valós szám és komplex szám is. A matematikában a 0-t olyan mennyiségnek tekintik, amely nulla mennyiségnek felel meg. Úgy is mondhatjuk, hogy a nulla az a “mennyiség”, amellyel egy olyan halmaz rendelkezik, amelynek nincsenek tagjai.

Az algebrában

Az elemi algebrában a nullát gyakran úgy fejezik ki, hogy az a számegyenes közepén fekszik. A 0 számot páros számnak tekintik, mivel a 2 szám egész számú többszöröse (2×0=0). A 0 nem prímszám, mert végtelen számú tényezője van, és nem összetett szám, mert két prímszám szorzata nem egyenlő a 0-val.

A 4 fő aritmetikai operátorral (+, -, ×, ÷) és az exponensművelettel szemben a 0 szám a következő szabályok szerint viselkedik:

• Adalékolás: x+0=0+x=x. A nullát additív azonossági elemnek tekintjük, mivel bármely szám plusz vagy mínusz nulla egyenlő azzal a számmal
• Húzás: x-0=x és 0-x=-x
• Sokszorzás: x⋅0=0⋅x=0. Bármely szám szorozva 0-val szintén egyenlő 0-val.
• Elosztás: 0/x=0, kivéve, ha x=0. Az x/0 matematikailag nem definiált mennyiség, mivel a 0-nak nincs multiplikatív inverze (egyetlen szám szorozva 0-val sem ad 1-et).
• Exponensek: x0=1, kivéve, ha x=0. Régóta vita van arról, hogy a 00 nem definiált vagy jól formált kifejezés. Minden pozitív x esetén 0x=0.

A határértékekkel kapcsolatos kifejezésekben a 0/0 mennyiség felbukkanhat olyan racionális függvények határértékeinek bemutatásával összefüggésben, mint f(x)/g(x). Ezekben az esetekben a 0/0 nem meghatározatlan, hanem egy határozatlan alakot jelent. Ez nem azt jelenti, hogy a határérték meghatározatlan, hanem azt, hogy azt más módszerrel kell kiszámítani, például deriváltak keresésével. Léteznek olyan algebrai modellek, ahol a nullával való osztás meghatározott mennyiséget ad, mint például a projekcionálisan kiterjesztett valós egyenes vagy a Riemann-gömb.

A halmazelméletben

A halmazelméletben a 0 szám az “üres halmaz” vagy a “nullhalmaz” kardinalitásának felel meg (általában {} vagy {∅} alakban ábrázolják. Egy halmaz kardinalitása az adott halmaz elemeinek száma, ha nincs narancs, akkor 0 narancsból álló halmazunk van (a narancsok üres halmaza).

A nullát gyakran használják kiindulópontként a halmazelméletben a többi természetes szám felépítéséhez. Ezek a von Neumman-konstrukciók, amelyek a neves polihisztor John von Neumannról kapták a nevüket, a természetes számokat a 0={} meghatározásával konstruálják, és definiálnak egy utódfüggvényt S(a) = a ∪ {a}. A természetes számok összessége az utódfüggvény rekurzív alkalmazásaiból konstruálható az üres halmazzal kezdve:

0 = {}

1 = 0 ∪ {0} = {0} = {{}}

2 = 1 ∪ {1} = {0,1} = {{}, {{}}}}

3 = 2 ∪ {2} = {0, 1, 2} = {{}, {{}}}, {{}}, {{}}}}

és így tovább. Ezt a mintát követve felépíthetjük a természetes számok teljes végtelen halmazát. Ily módon azt mondhatjuk, hogy minden egyes természetes számnak megfelel az előtte lévő összes természetes számot tartalmazó halmaz.

A fizikában

A fizikában a mennyiségi mérések elvégzésével összefüggésben a 0-t tekintjük annak az alapértéknek, amelyből minden más egységmérés kiindul. Nagyon gyakran a 0 alapvonala valamilyen fizikailag jelentős változónak felel meg, amely természetesen megkülönböztethető az összes többi mérési nagyságtól.

A Kelvin-skálán például a 0 K hőmérséklet az abszolút 0-nak felel meg – a fizikailag lehetséges leghidegebb hőmérsékletnek. A Celsius-féle hőmérsékleti skálán a 0 °C a víz fagyáspontját jelenti légköri nyomáson. A dinamikában és az elektromágnesességben a 0 érték azt a helyzetet jelöli, amelyben egy rendszer a lehető legkisebb potenciális energiával rendelkezik. Például egy atom alapállapotához, az atomban lévő elektronok lehető legalacsonyabb energiaszintjéhez gyakran 0 értéket rendelnek.

Hasonlóképpen, a kinematika összefüggésében azt a vonatkoztatási rendszert, amelyből a mozgás megfigyelését végzik, úgy határozzák meg, hogy a középpontja a koordinátatengely origóján, a (0, 0) pontban van. Az olyan konzervált mennyiségek esetében, mint a tömeg-energia, az impulzus és a szögimpulzus, a konzervált mennyiségek változásának teljes összege egy izolált rendszerben mindig egyenlő 0-val.

A számítástechnikában

A számítógépek az információt bitek hosszú, 1-ekből és 0-kból álló sorozatok formájában tárolják. Ebben a bináris ábrázolásban a 0 megfelel a “kikapcsolt” pozíciónak, és szemben áll az 1 által jelölt “bekapcsolt” pozícióval. 0 érték egy elektromos áramkörben azt jelenti, hogy az áramkör ki van kapcsolva, és nincs elektromos áramlás. Hasonlóképpen, számos számítási logika a “0”-t a hamis igazságértéket jelentő karakterként határozza meg.

A számítógépes adatbázisokban egy tömb elemeinek számolása nulla alapú számolási rendszerrel történik. Ez azt jelenti, hogy egy n elemű halmaz esetében az elemek indexei 0-val kezdődnek. Így a 0 indexszámú elem valójában a sorozat első eleme, az 1 indexszámú pedig a második elemnek felel meg, és így tovább. Általában egy halmaz n-edik tagjának indexszáma n-1-nek felel meg. Ez a számolási rendszer zavart okozhat az új programozók számára, akik hozzászoktak ahhoz, hogy intuitív módon az 1-től kezdődő indexértékeket rendelik hozzá.