La variance est un nombre qui indique à quel point un ensemble de nombres est éloigné les uns des autres.La variance est identique à l’écart-type au carré et exprime donc « la même chose » (mais plus fortement).
Variance – Exemple
Une étude fait réaliser à 100 personnes une tâche de vitesse simple pendant 80 essais. Pour chaque participant, 80 temps de réaction (en secondes) sont ainsi enregistrés. Une partie de ces données est présentée ci-dessous.

Dans les études de ce type, on constate généralement que les personnes deviennent plus rapides à mesure qu’elles effectuent la tâche de vitesse plus souvent. C’est-à-dire que le temps de réaction moyen a tendance à diminuer au fil des essais.
De même, les temps de réaction varieront typiquement moins entre différentes personnes dans la mesure où elles effectuent la tâche plus souvent. Techniquement, on dit que la variance diminue au fil des essais. Le tableau ci-dessous illustre cela pour les essais 1,4,7 et 10.
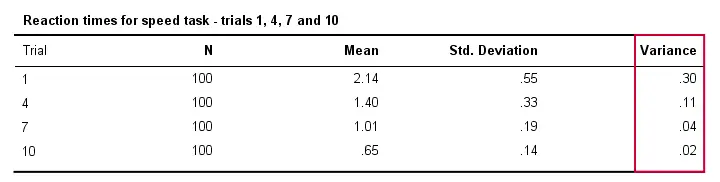
Variance et histogramme
Une excellente façon de visualiser les données de notre tableau précédent est un histogramme pour chaque essai. Ainsi, la figure ci-dessous illustre le fait que les participants sont devenus plus rapides au fil des essais ; de l’essai 1 à l’essai 10, les barres de l’histogramme se déplacent vers la gauche, vers 0 seconde.
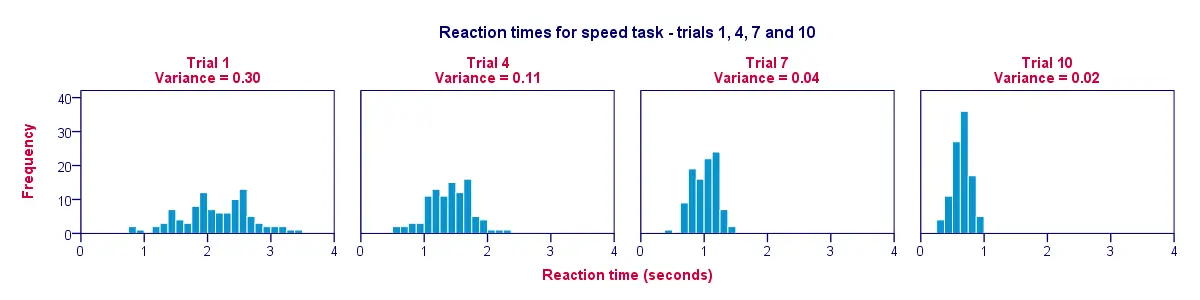
Un deuxième constat est que les histogrammes deviennent plus étroits (et donc plus élevés) au fur et à mesure que nous passons de l’essai 1 à l’essai 10 ; cela illustre le fait que les temps de réaction varient de moins en moins entre nos participants au fur et à mesure que l’expérience progresse. La variance diminue au fil des essais.
Variance – Formule de population
Une formule de base pour calculer la variance est
$S^2 = \frac{\sum(X – \overline{X})^2}{n}$
Nous vous recommandons d’essayer de comprendre ce que fait cette formule car cela aide beaucoup à comprendre l’ANOVA (= analyse de la variance). Nous allons donc la démontrer sur une simple poignée de données.
Variance – GoogleSheets
Pour simplifier, nous allons réduire nos données au premier essai des 5 premiers participants. Ces 5 temps de réaction -et un calcul manuel de leur variance- se trouvent dans cette GoogleSheet.
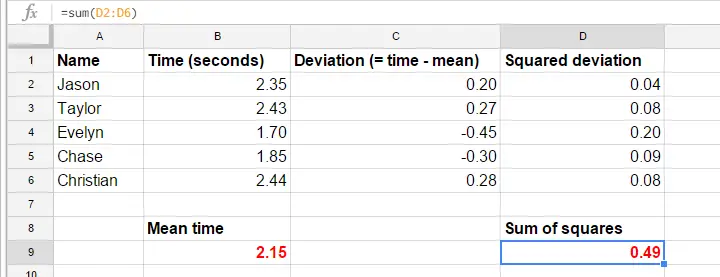
Variance – Étapes de calcul
Les formules de la GoogleSheet montrent précisément comment calculer une variance. Les étapes de base sont
- calculer le temps de réaction moyen (2,15);
- calculer les scores d’écart (temps de réaction moins temps de réaction moyen);
- calculer les scores d’écart au carré;
- additionner les scores d’écart au carré. Le résultat (0,49) est une somme de carrés, le principal élément constitutif de l’ANOVA;
- diviser la somme de carrés par le nombre d’observations (5 temps de réaction).
Alternativement, calculer une variance en tapant =VARP(B2:B6) dans une certaine cellule (B2:B6 sont les cellules qui contiennent nos 5 temps de réaction). VARP est l’abréviation de « population de variance ». OpenOffice et MS Excel contiennent des formules similaires.
Variance – Formule d’échantillon
Comme pour l’écart-type, si nos données sont un simple échantillon aléatoire d’une population beaucoup plus grande, la formule susmentionnée sous-estimera systématiquement la variance de la population. Dans ce cas, nous utiliserons une formule légèrement différente :
$S^2 = \frac{\sum(X_i – \overline{X})^2}{n – 1}$
La formule à utiliser dépend donc de nos données : contiennent-elles toute la population que nous aimerions étudier ou sont-elles un simple échantillon de cette population ?
Puisque nos 100 participants sont clairement un échantillon, nous utiliserons la formule de l’échantillon. Dans GoogleSheets, taper =VAR(B2:B6) dans une certaine cellule renverra la variance de l’échantillon.
Variance dans SPSS
Pour autant que nous le sachions, la formule de la variance de la population est complètement absente de SPSS et nous considérons cela comme un grave défaut. Au lieu de cela, SPSS utilise toujours la formule de l’échantillon.Cela vaut pour la variance entre les sujets (abordée dans ce tutoriel) ainsi que pour la variance au sein des sujets. La sortie pertinente est présentée ci-dessous.

En ce qui concerne ce tableau de sortie, notez également que la variance est effectivement l’écart type au carré (à part les arrondis).
En ce qui concerne la variance, c’est à peu près tout. Nous espérons que ce tutoriel vous a aidé à comprendre ce qu’est une variance.
>