Définitions des statistiques >Test de Friedman
Qu’est-ce que le test de Friedman ?
Le test de Friedman est un test non paramétrique pour trouver les différences de traitements entre plusieurs essais. Nonparamétrique signifie que le test ne suppose pas que vos données proviennent d’une distribution particulière (comme la distribution normale). Fondamentalement, il est utilisé à la place du test ANOVA lorsque vous ne connaissez pas la distribution de vos données.
Le test de Friedman est une extension du test des signes, utilisé lorsqu’il y a plusieurs traitements. En fait, s’il n’y a que deux traitements, les deux tests sont identiques.
Réaliser le test
Vos données doivent répondre aux exigences suivantes :
- Les données doivent être ordinales (par ex. l’échelle de Likert) ou continues,
- Les données proviennent d’un seul groupe, mesurées à au moins trois occasions différentes,
- L’échantillon a été créé avec une méthode d’échantillonnage aléatoire,
- Les blocs sont mutuellement indépendants (i.c’est-à-dire que toutes les paires sont indépendantes – l’une n’affecte pas l’autre),
- Les observations sont classées au sein des blocs sans égalité.
L’hypothèse nulle du test est que les traitements ont tous des effets identiques, ou que les échantillons diffèrent d’une manière ou d’une autre. Par exemple, ils ont des centres, des étalements ou des formes différents. L’hypothèse alternative est que les traitements ont effectivement des effets différents.
Préparez vos données pour le test.
Etape 1 : triez vos données en blocs (colonnes dans une feuille de calcul).Pour cet exemple, nous avons 12 patients recevant trois traitements différents.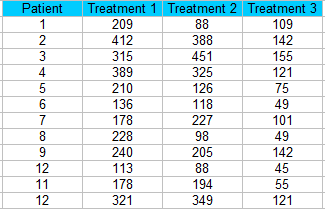
Etape 2 : Classez chaque colonne séparément. Le plus petit score devrait obtenir un rang de 1. Je fais un classement à travers les lignes ici, donc chaque patient est classé à 1, 2 ou 3 pour chaque traitement.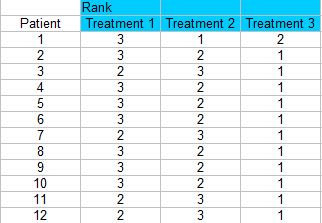
Étape 3 : Additionnez les rangs (trouvez un total pour chaque colonne).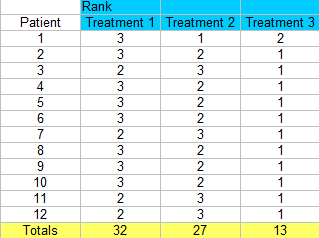
Exécuter le test
Note : Ce test n’est généralement pas exécuté à la main, car les calculs prennent du temps et demandent beaucoup de travail. Presque tous les progiciels statistiques populaires peuvent exécuter ce test. Cependant, j’inclus ici les étapes manuelles à titre de référence.
Etape 4 : calculer la statistique de test. Vous aurez besoin de :
- n : le nombre de sujets (12)
- k : le nombre de traitements (3)
- R : le total des rangs pour chacune des trois colonnes (32, 27, 13).
Insérez-les dans la formule suivante et résolvez :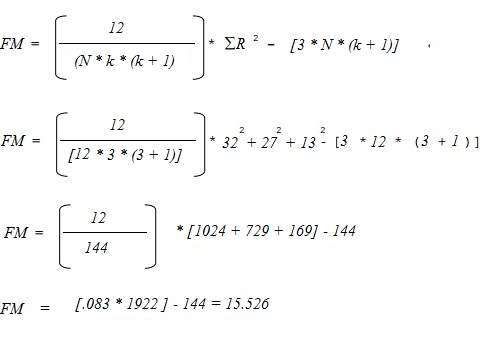
Étape 5 : Trouvez la valeur critique de FM à partir du tableau des valeurs critiques de Friedman (voir tableau ci-dessous).
Utilisez le tableau k=3 (car c’est le nombre de traitements que nous avons) et un niveau alpha de 5%. Vous pourriez choisir un niveau alpha plus élevé ou plus bas, mais 5% si assez commun – donc utilisez la table de 5% si vous ne connaissez pas votre niveau alpha.
En regardant n-12 dans ce tableau, nous trouvons une valeur critique FM de 6,17.
Étape 6 : Comparez la statistique de test FM calculée (étape 4) à la valeur critique FM (étape 5). Rejeter l’hypothèse nulle si la valeur F calculée est supérieure à la valeur critique FM.:
- Statistique de test FM calculée = 15,526.
- Valeur critique FM du tableau = 6,17.
La statistique FM calculée est plus grande, donc vous rejetteriez l’hypothèse nulle.
Tableau des valeurs critiques de l’ANOVA de Friedman par rangs
Trois tableaux selon « k ».
Si votre k est supérieur à 5, ou si votre n est supérieur à 13, utilisez le tableau des valeurs critiques du chi carré à l’étape 5 pour obtenir la valeur critique.
k=3
| N | α <.10 | α ≤.05 | α <.01 |
| 3 | 6.00 | 6.00 | – |
| 4 | 6.00 | 6.50 | 8.00 |
| 5 | 5.20 | 6.40 | 8.40 |
| 6 | 5.33 | 7.00 | 9.00 |
| 7 | 5.43 | 7.14 | 8.86 |
| 8 | 5.25 | 6.25 | 9.00 |
| 9 | 5.56 | 6.22 | 8.67 |
| 10 | 5.00 | 6.20 | 9.60 |
| 11 | 4.91 | 6.54 | 8.91 |
| 12 | 5.17 | 6.17 | 8.67 |
| 13 | 4.77 | 6,00 | 9,39 |
| ∞ | 4,61 | 5,99 | 9,21 |
k=4
| N | α <.10 | α ≤.05 | α <.01 |
| 2 | 6.00 | 6.00 | – |
| 3 | 6.60 | 7.40 | 8.60 |
| 4 | 6.30 | 7.80 | 9.60 |
| 5 | 6.36 | 7.80 | 9.96 |
| 6 | 6.40 | 7.60 | 10.00 |
| 7 | 6.26 | 7.80 | 10.37 |
| 8 | 6.30 | 7.50 | 10.35 |
| ∞ | 6.25 | 7.82 | 11.34 |
k=4
| N | α <.10 | α ≤.05 | α <.01 |
| 3 | 7.47 | 8.53 | 10.13 | 4 | 7.60 | 8.80 | 11.00 | 5 | 7.68 | 8.96 | 11.52 | ∞ | 7.78 | 9.49 | 13,28 |
Référence:
Analyse bidirectionnelle de la variance par rangs de Friedman – Analyse des données de k-within-group avec une
variable de réponse quantitative. Récupéré le 7-17-2016 de : http://psych.unl.edu/psycrs/handcomp/hcfried.PDF
Stephanie Glen. « Test de Friedman / Analyse de la variance à deux voies par les rangs » De StatisticsHowTo.com : Des statistiques élémentaires pour le reste d’entre nous ! https://www.statisticshowto.com/friedmans-test/
——————————————————————————
Vous avez besoin d’aide pour un devoir ou une question de test ? Avec Chegg Study, vous pouvez obtenir des solutions étape par étape à vos questions de la part d’un expert dans le domaine. Vos 30 premières minutes avec un tuteur Chegg sont gratuites !