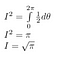Lord Kelvin a écrit à propos de cette intégrale : « Un mathématicien est quelqu’un pour qui cela est aussi évident que le fait que deux fois deux font quatre l’est pour vous. »
Amusez-vous 😉
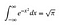
OK, donc je vais supposer que vous connaissez quelques notions d’intégration et de différentiation. Ce qui suit ajoutera un peu d’intuition à des trucs astucieux qui viendront plus tard. Ne vous inquiétez pas si certains d’entre eux sont légèrement déconcertants, essayez juste d’avoir une idée de ce qui se passe.
La stratégie ici sera de faire une substitution astucieuse. Mais nous allons faire une substitution dans deux variables. Vous pouvez visualiser le problème actuel comme le calcul de l’aire sous une courbe
Mais nous allons montrer que le problème peut être transformé en un problème de calcul d’un volume.
Pour calculer le volume, nous utilisons une formule de changement de variable légèrement différente de celle que vous utilisez dans les intégrales normales. Nous allons utiliser les coordonnées polaires. Cela exprime les coordonnées x et y en termes de rayon et d’angle. Geogebra a une belle façon interactive de le voir ici

Puis nous allons utiliser la formule magique de changement de base pour les coordonnées polaires.
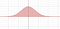
Lors du calcul de l’aire sous la courbe, nous avions l’élément ‘dx’ qui représente une petite distance le long de l’axe x. Lors du calcul d’un volume, nous avons dx dy, qui est comme un petit rectangle avec une longueur de côté dx et dy. Nous utilisons ensuite ces bases pour créer une série de cases qui estiment le volume. La visualisation ci-dessous est la plus facile à comprendre. L’intégrale est la limite de ces approximations.
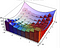
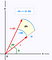
Lorsque, au contraire, nous utilisons le système de coordonnées polaires, nous avons un élément d’aire légèrement différent en dessous. Ci-dessous, dA est l’élément de surface. En modifiant légèrement l’angle et le rayon, cet élément d’aire peut être de mieux en mieux approché par un rectangle dont les côtés sont respectivement de longueur dr et r*dtheta. Si vous êtes à l’aise avec un peu de géométrie, pour de petits thêta sin(thêta) est très bien approximé par thêta et vous pouvez alors prouver le résultat ci-dessous.
Résolution de l’intégrale
D’abord nous donnons un nom à notre intégrale. Nous l’appelons I.
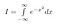
Notez que x est juste une ‘variable fictive’. La zone existe quel que soit le nom de variable que nous utilisons. Donc, nous pouvons aussi écrire les deux équations suivantes
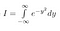
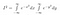
Maintenant, comme I est juste une constante, bien que nous ne connaissions pas encore sa valeur, nous pouvons utiliser nos règles normales pour amener une constante à l’intérieur d’une intégrale
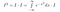
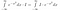
Pour l’instant, nous n’avons pas fait beaucoup de travail de fond. Maintenant, nous réfléchissons sérieusement à ce que signifie l’intégrale. Nous prenons des intégrales de fonctions. Si deux fonctions prennent partout la même valeur, elles sont identiques, et ont la même aire. Avec cela en tête, nous pouvons faire les manipulations suivantes, si nous considérons I*exp(-x²) comme une fonction de x, c’est-à-dire quelque chose qui prend des valeurs de x en entrée, et donne un nombre en sortie.
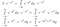
Ok, c’était beaucoup à assimiler. Dans la première ligne, nous avons juste réécrit I sous sa forme intégrale avec un nom de variable différent. Dans la deuxième ligne, en traitant I*exp(-x²) comme une fonction, nous avons réalisé que nous pouvions faire entrer l’exp(-x²) à l’intérieur de l’intégrale dy, et que cela donnerait toujours la même valeur de sortie pour n’importe quelle valeur d’entrée de x. Enfin, nous avons utilisé les règles de l’exponentiation.
En écrivant cela en entier, nous avons maintenant
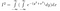
Vient ensuite l’intuition qui tue. Plus haut, nous avons joué avec les noms de variables et la façon de représenter une fonction. Maintenant, nous changeons de perspective : cette expression représente également l’intégrale de exp(-(y²+x²)) sur l’ensemble du plan 2D, avec l’élément d’aire dA = dx dy. C’est-à-dire que dx dy est un petit rectangle sur un plan, et exp(-(y²+x²)) est la hauteur au-dessus de ce rectangle.
Puis, nous utilisons les connaissances en coordonnées polaires de tout à l’heure
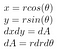
Comme sin² + cos² = 1, après avoir tout branché, on obtient
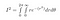
r va de 0 à l’infini et thêta va de 0 à 2*pi, car cela couvre tout le plan 2D : tout point a un rayon inférieur à l’infini, et un angle compris entre 0 et 2pi radians.
Nous pouvons évaluer l’intégrale interne en utilisant la règle de la chaîne
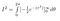
Et, dans la terre promise, nous nous trouvons maintenant :