Les événements aléatoires qui se déroulent dans un espace échantillon continu peuvent invoquer l’imagerie géométrique pour au moins deux raisons : en raison de la nature du problème ou en raison de la nature de la solution.
Certains problèmes, comme l’aiguille de Buffon, les oiseaux sur un fil, le paradoxe de Bertrand ou le problème du bâton cassé en trois morceaux se posent, par nature, dans un cadre géométrique. Ce dernier admet également de multiples reformulations qui nécessitent la comparaison des aires des figures géométriques. En général, nous pouvons considérer les probabilités géométriques comme des quantités non négatives (ne dépassant pas 1) affectées à des sous-régions d’un domaine donné sous réserve de certaines règles. Si la fonction μ est une expression de cette affectation définie sur un domaine D, alors, par exemple, nous exigeons
0 ≤ μ(A) ≤ 1, A ⊂ D et
μ(D) = 1
La fonction μ n’est généralement pas définie pour tous les A ⊂ D. Ces sous-ensembles de D pour lesquels μ est définie sont les événements aléatoires qui forment un espace d’échantillonnage particulier. Très souvent, μ est défini au moyen du rapport des aires, de sorte que, si σ(A) est défini comme « l’aire » de l’ensemble A, alors on peut fixer μ(A) = σ(A) / σ(D).
Problème 1
Deux amis qui prennent le métro pour se rendre à leur travail depuis la même station arrivent à la station de façon uniformément aléatoire entre 7 et 7h20 du matin. Ils acceptent de s’attendre mutuellement pendant 5 minutes, après quoi ils prennent un train, qu’ils soient ensemble ou seuls. Quelle est la probabilité de leur rencontre à la station ?
Dans un système cartésien de coordonnées (s, t), un carré de côté 20 (minutes) représente toutes les possibilités d’arrivées matinales des deux amis à la station de métro.

La zone grise A est délimitée par deux droites, t = s + 5 et t = s – 5, de sorte qu’à l’intérieur de A, |s – t| ≤ 5. Il s’ensuit que les deux amis ne se rencontreront qu’à condition que leurs arrivées s et t tombent dans la région A. La probabilité que cela se produise est donnée par le rapport entre l’aire de A et les are du carré :
/ 400 = 175/400 = 7/16.
Problème 2
(.)
Trois points A, B, C sont placés au hasard sur un cercle de rayon 1. Quelle est la probabilité que ΔABC soit aigu ?.
Fixer le point C. Les positions des points A et B sont alors définies par des arcs α et β partant de C dans deux directions. A priori, nous savons que 0 < α + β < 2π. Les valeurs favorables pour notre problème de α et β (en tant qu’angles aigus sous-tendus satisfont) 0 < α < π et 0 < β < π. Leur somme ne peut être inférieure à π car cela rendrait l’angle C obtus, donc α + β > π. La situation est présentée dans le schéma suivant où le carré a pour côté 2π.
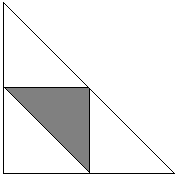
La région D est l’intersection de trois demi-plans : 0 < α, 0 < β, et α + β < 2π. C’est le grand triangle dans le diagramme ci-dessus. Les événements favorables appartiennent au triangle grisé qui est l’intersection des demi-plans α < π, β < π, et α + β > π. Le rapport des aires des deux est évidemment 1/4.
Observez maintenant, qu’à moins que le triangle aléatoire soit aigu, il peut être considéré comme obtus puisque la probabilité que deux des trois points A, B, C forment un diamètre est 0. (Pour que BC soit un diamètre, il faudrait avoir α + β = π qui est une droite, avec zéro comme seule affectation possible de l’aire). On peut donc dire que la probabilité que ΔABC soit obtus est de 3/4. Pour un triangle obtus, le cercle peut être divisé en deux moitiés, le triangle étant entièrement situé dans l’une des moitiés. Il s’ensuit que 3/4 est la réponse à la question suivante :
Trois points A, B, C sont placés au hasard sur un cercle de rayon 1. Quelle est la probabilité que tous les trois se trouvent dans un demi-cercle ?
- E. J. Barbeau, Murray S. Klamkin, W. O. J. Moser, Cinq cents défis mathématiques par (MAA, 1995, problème 244.)
- D. A. Klain, G.-C. Rota Introduction à la probabilité géométrique , Cambridge University Press, 1997
- A. A. Sveshnikov, Problèmes de théorie des probabilités, statistique mathématique et théorie des fonctions aléatoires, Dover, 1978
- A. M. Yaglom, I. M. Yaglom, Challenging Mathematical Problems With Elementary Solutions, Dover, 1987
- Probabilités géométriques
- La plupart des triangles sont-ils obtus ?
- Huit sélections dans six secteurs
- Trois points aléatoires sur un cercle
- Probabilité géométrique
- Bâton brisé en trois morceaux (coordonnées trilinéaires)
- Bâton brisé en trois morceaux. Solution en coordonnées cartésiennes
- Paradoxe de Bertrand
- Oiseaux sur un fil (problème et simulation interactive)
- Oiseaux sur un fil : Solution de Nathan Bowler
- Des oiseaux sur un fil. Solution de Mark Huber
- Oiseaux sur un fil : une simulation probabiliste. Solution de Moshe Eliner
- Des oiseaux sur un fil. Solution de Stuart Anderson
- Des oiseaux sur un fil. Solution de Bogdan Lataianu
- Simulation de nouilles de Buffon
- Moyennage de gouttes de pluie – un exercice de probabilité géométrique
- Moyennage de gouttes de pluie, partie 2
- Rectangle sur un échiquier : Une introduction
- Marquer et briser des bâtons
- Points aléatoires sur un segment
- Couverture d’un demi-cercle
- Couverture d’un hémisphère
- Intervalles aléatoires superposés
- Intervalles aléatoires. avec une dominante
- Points sur une grille carrée
- Probabilités planes sur une sphère
- Probabilité dans un triangle
|Contact|||Première page||Contenu||Haut|
Copyright © 1996-…2018 Alexander Bogomolny