Le modèle d’Ising est un exemple particulier de système thermodynamique, et c’est le système modèle pour comprendre les transitions de phase. Vous savez que tant de biologistes passent beaucoup de temps avec de minuscules mouches à fruits ? Eh bien, les physiciens passent beaucoup de temps avec le modèle d’Ising. Comme nous le dit utilement le professeur Raghu, c’est la drosophile des transitions de phase.

Personnellement, je ne suis pas le plus grand fan de son analogie car je trouve que les mouches à fruits sont dégoûtantes. Espérons que le modèle d’Ising ne sera pas trop grossier.

Motivation

Pourquoi devrions-nous passer autant de temps à parler du modèle d’Ising ?

• Il est étonnamment utile pour nous aider à penser à toutes sortes de comportements liés aux transitions de phase. Par exemple :

  • le modèle d’Ising présente une rupture de symétrie en phase à basse température (dont nous venons de parler)

  • il a un « point critique » spécial à une température bien définie (auquel nous avons fait allusion dans le diagramme de phase de l’eau)

  • autres caractéristiques riches.

• C’est l’un des rares modèles exactement solvables où nous pouvons réellement calculer des quantités thermodynamiques et les interpréter.

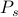  • En général, le calcul des quantités thermodynamiques est difficile parce que vous devez additionner de nombreux termes. Rappelez-vous de notre premier cours de thermo que vous pouvez penser à un système d’équilibre comme un ensemble de nombreux états , chacun pondéré avec leur propre probabilité . Dans ce cadre, les quantités thermodynamiques que vous observez correspondent à des moyennes sur l’ensemble. En particulier, si vous voulez trouver la moyenne d’ensemble d’une certaine observable 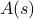, vous devez trouver la somme 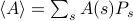, où la somme court sur tous les états possibles. Le problème avec ceci, comme vous vous en souvenez, est que le nombre d’états d’un système thermodynamique s’échelonne exponentiellement avec le nombre de particules ! Même pour un système de taille modérée, il y a juste trop d’états pour qu’un ordinateur puisse explicitement calculer la moyenne – sans parler d’un système thermodynamique où 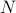est de l’ordre de .

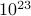  • On doit donc  »être intelligent » pour calculer la fonction de partition, et nous devrions être reconnaissants pour les systèmes exactement solvables !

• Le modèle d’Ising est simple, mais il peut être appliqué à un nombre surprenant de systèmes différents.

  • C’est notre premier goût d’universalité – une caractéristique des phénomènes critiques où la même théorie s’applique à toutes sortes de transitions de phase différentes, que ce soit dans les liquides et les gaz ou les aimants ou les supraconducteurs ou autre. Les physiciens adorent ce genre de comportement général car il suggère une sorte d’ordre plus profond dans notre monde chaotique.

Définition du modèle d’Ising

Le modèle d’Ising est un modèle mathématique qui ne correspond pas à un système physique réel. C’est un immense treillis (carré) de sites, où chaque site peut être dans l’un des deux états. Nous étiquetons chaque site avec un indice , et nous appelons les deux états et . Pour dire que le ème site est dans l’état , nous écrivons .

Nouveau, cette définition est terriblement abstraite et non physique, donc pour nous, physiciens, il est extrêmement utile d’avoir un système réel à l’esprit, afin que nous puissions nous référer à quelque chose d’explicite et construire une intuition physique. Voici quelques systèmes physiques que le modèle d’Ising pourrait représenter :

• Un aimant. Chaque site représente un  » spin  » particulier dans le matériau (un électron non apparié ? ?), et il est si le spin pointe vers le bas ou si le spin pointe vers le haut. Chacun des spins agit comme un mini-aimant avec son propre mini-moment magnétique ; si tous les spins sont alignés, alors l’ensemble du réseau de spins se comporte comme un gros aimant avec un moment magnétique macroscopique net.

• Un alliage ; disons, du laiton. Chacun des sites est un atome dans le réseau ; représente un atome de cuivre à ce site ; représente le zinc.

• Un  »gaz de réseau ». Chacun des sites est l’emplacement possible d’une particule ; signifie que ce site est vide et signifie que ce site est occupé par une particule.

• Des réseaux de vortex bactériens ????

Pour l’instant, nous allons considérer le modèle d’Ising comme un modèle d’aimant. C’est un modèle grossièrement simplifié et jouet d’un aimant, c’est sûr, mais l’analogie de l’aimant peut néanmoins aider à guider notre intuition physique chérie.

Constituer le hamiltonien

Une question naturelle à poser sur ce modèle Mickey-mouse d’un aimant est de savoir quelle énergie il possède. Pour être plus précis, nous voulons écrire une fonction qui représente l’énergie de chaque configuration possible (alias micro-état) des spins dans l’aimant. Comme nous le savons, cette fonction d’énergie est appelée le hamiltonien.

Dans le modèle d’Ising, le hamiltonien comprend deux types d’interactions :

• le terme de champ externe. Comme nous nous souvenons de la mécanique quantique, un champ magnétique externe peut diviser les énergies de l’état spin down et spin up, de sorte que l’un est plus élevé en énergie et l’autre est plus faible.

  • La taille de représente la force du champ, elle vous indique donc de combien un spin est plus élevé en énergie que l’autre.

  • Le signe de vous indique si c’est le spin up ou le spin down qui est préféré.

  • Puisque chaque spin individuel ressent le champ externe, nous devons faire la somme de tous les sites pour trouver la contribution totale à l’énergie.

• le terme d’interaction entre les spins voisins – peut-être veulent-ils s’aligner les uns sur les autres et pointer dans la même direction, peut-être veulent-ils s’anti-aligner et pointer dans des directions différentes. Physiquement, nous pouvons imaginer que cette interaction se produit parce que chaque spin dans l’aimant est son propre mini dipôle magnétique qui établit son propre champ magnétique, et ses voisins peuvent sentir ce champ magnétique.

  • La taille de vous indique à quel point les spins voisins sont couplés les uns aux autres – à quel point ils veulent s'(anti-)aligner. Physiquement, la force du couplage spin-spin pourrait dépendre de la distance entre eux dans la lattique du maget, par exemple.

  • Le signe de vous indique si les voisins préfèrent s’aligner ou s’anti-aligner. (Le terme technique pour cela est ferromagnétique ou anti-ferromagnétique, respectivement). Physiquement, le fait qu’un matériau soit l’un ou l’autre (ou ni l’un ni l’autre) dépend des détails exacts de mécanique quantique sur la façon dont les spins interagissent.

  • Puisque l’interaction spin-spin se produit entre deux spins, nous devons faire la somme sur les paires de sites pour trouver son interaction totale à l’énergie.

Plus sur le terme d’interaction

Une question naturelle sur le terme d’interaction spin-spin est de savoir quels spins sont couplés à quels spins ?

Si nous revenons à nouveau à l’image physique de l’aimant, et que nous zoomons sur un spin particulier, nous nous attendrions à ce que la force de l’interaction spin-spin soit plus forte pour les spins proches et plus faible pour les spins éloignés. La dépendance exacte de la distance des interactions spin-spin est probablement assez compliquée pour les aimants réels.

Pour le modèle d’Ising, nous faisons l’hypothèse la plus simple possible pour la nature de cette interaction spin-spin :

Quelques commentaires:

• Dans un treillis carré de dimensions, chaque site a 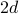voisins les plus proches : gauche et droite dans une dimension, haut et bas une fois que l’on ajoute la deuxième dimension, etc…

• Nous supposons que l’interaction est isotrope – tous les voisins sont traités de la même manière quelle que soit la direction.

• Nous parlons souvent des interactions entre voisins les plus proches comme de l’énergie d’une liaison qui relie deux sites du réseau.

• Lorsque nous additionnons sur des paires de sites adjacents, symboliquement, nous écrivons de petits crochets autour des indices pour représenter  »le plus proche voisin ».

Une conséquence agréable des interactions de plus proche voisin est que lorsque nous trouvons l’énergie totale d’une certaine configuration de spins, plutôt que d’additionner sur toutes les paires de sites possibles, nous additionnons seulement sur les paires de sites qui sont adjacents les uns aux autres.

Maintenant que nous avons discuté de toutes ces choses, nous sommes prêts à écrire l’expression réelle de l’hamiltonien. (Je voulais expliquer et interpréter la physique avant d’écrire l’hamiltonien afin que les symboles aient une sorte de sens.)

Hamiltonien du modèle d’Ising

L’hamiltonien du modèle d’Ising peut s’écrire comme

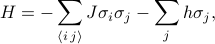
où représente l’interaction spin-spin, représente le champ externe, et les 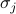sont les spins individuels sur chacun des sites du réseau. La première somme est calculée sur toutes les paires de sites de treillis voisins (aussi appelés liaisons) ; elle représente les interactions entre les spins. La seconde somme est sur tous les sites de treillis eux-mêmes ; elle représente le champ externe qui essaie d’aligner tous les spins dans une direction.

Poursuivez sur la thermodynamique du modèle d’Ising.