La convolution non désirée est un problème inhérent au transfert d’informations analogiques. Par exemple, tout ce qui suit peut être modélisé comme une convolution : le flou de l’image dans une caméra tremblante, les échos dans les appels téléphoniques longue distance, la bande passante infinie des capteurs analogiques et de l’électronique, etc. La déconvolution est le processus de filtrage d’un signal pour compenser une convolution indésirable. L’objectif de la déconvolution est de recréer le signal tel qu’il existait avant la convolution. Cela nécessite généralement de connaître les caractéristiques de la convolution (c’est-à-dire la réponse impulsionnelle ou en fréquence). On peut distinguer cette méthode de la déconvolution aveugle, où les caractéristiques de la convolution parasite ne sont pas connues. La déconvolution aveugle est un problème beaucoup plus difficile qui n’a pas de solution générale, et l’approche doit être adaptée à l’application particulière.
La déconvolution est presque impossible à comprendre dans le domaine temporel, mais quitestra simple dans le domaine fréquentiel. Chaque sinusoïde qui compose le signal original peut être modifiée en amplitude et/ou en phase lorsqu’elle passe par la convolution indésirable. Pour extraire le signal original, le filtre de déconvolution doit annuler ces changements d’amplitude et de phase. Par
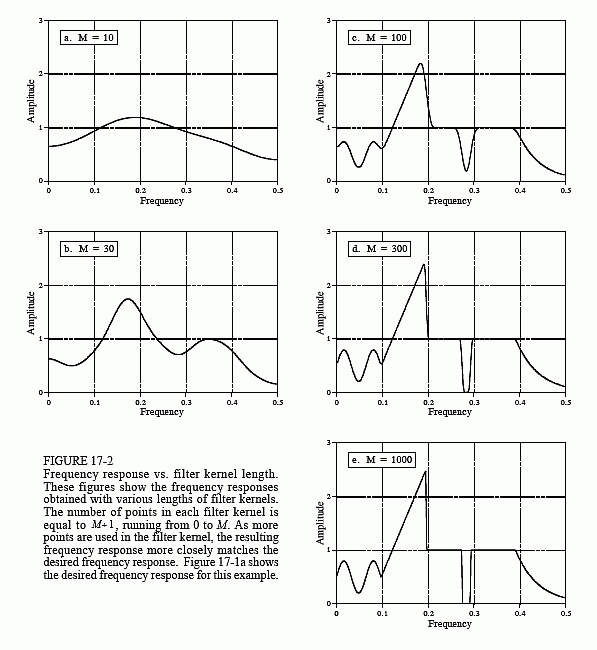
exemple, si la convolution change l’amplitude d’une sinusoïde de 0,5 avec un déphasage de 30 degrés, le filtre de déconvolution doit amplifier la sinusoïde de 2,0 avec un changement de phase de -30 degrés.
L’exemple que nous utiliserons pour illustrer la déconvolution est un détecteur de rayons gamma. Comme l’illustre la figure 17-3, ce dispositif est composé de deux parties, un scintillateuret un détecteur de lumière. Un scintillateur est un type spécial de matériau transparent, comme l’iodure de sodium ou le germanate de bismuth. Ces composés transforment l’énergie de chaque rayon gamma en un bref éclat de lumière visible. Cette lumière
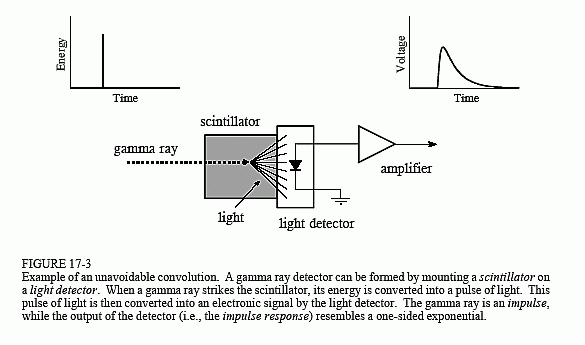
est ensuite convertie en un signal électronique par un détecteur de lumière, tel qu’une photodiode ou un tube photomultiplicateur. Chaque impulsion produite par le détecteur ressemble à une exponentielle unilatérale, avec quelques arrondis dans les coins. Cette forme est déterminée par les caractéristiques du scintillateur utilisé. Lorsque le rayon gamma dépose son énergie dans le scintillateur, les atomes voisins sont excités à un niveau d’énergie plus élevé. Ces atomes se désexcitent de manière aléatoire, produisant chacun un seul photon de lumière visible. Le résultat net est une impulsion lumineuse dont l’amplitude décroît sur quelques centaines de nanosecondes (pour l’iodure de sodium). Comme l’arrivée de chaque rayon gamma est une impulsion, l’impulsion de sortie du détecteur (c’est-à-dire l’exponentielle unilatérale) est la réponse impulsionnelle du système.
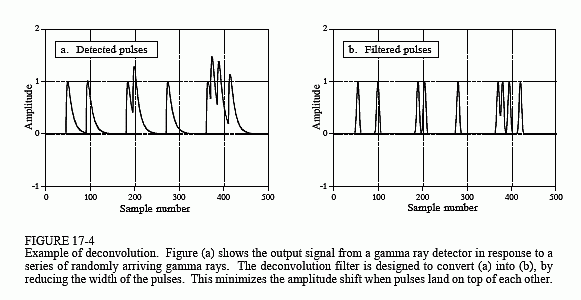
La figure 17-4a montre les impulsions générées par le détecteur en réponse à des rayons gamma arrivant de façon aléatoire. L’information que nous voudrions extraire de ce signal de sortie est l’amplitude de chaque impulsion, qui est proportionnelle à l’énergie du rayon gamma qui l’a générée. Il s’agit d’une information utile car l’énergie peut indiquer des choses intéressantes sur l’endroit où le rayon gamma est passé. Par exemple, elle peut fournir des informations médicales sur un patient, indiquer l’âge d’une galaxie lointaine, détecter une bombe dans les bagages d’une compagnie aérienne, etc.
Tout irait bien si on ne détectait qu’un rayon gamma occasionnel, mais ce n’est généralement pas le cas. Comme le montre la figure (a), deux ou plusieurs impulsions peuvent se chevaucher, décalant l’amplitude mesurée. Une solution à ce problème consiste à déconvoluer le signal de sortie du détecteur, en rendant les impulsions plus étroites afin de réduire le chevauchement. Idéalement, nous aimerions que chaque impulsion ressemble à l’impulsion d’origine. Comme vous pouvez vous en douter, ce n’est pas possible et nous devons nous contenter d’une impulsion de longueur finie, mais nettement plus courte que l’impulsion détectée. Cet objectif estillustré à la figure 17-4b.
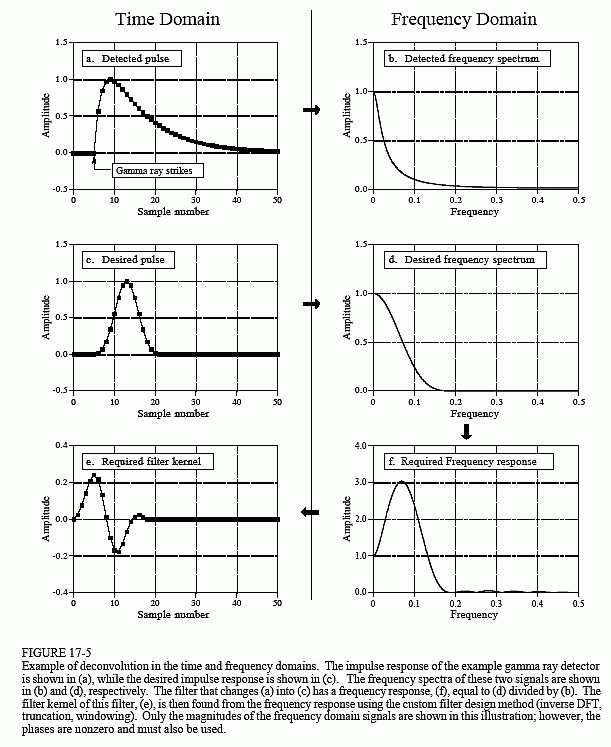
Même si le signal du détecteur a son information codée dans le domaine temporel,une grande partie de notre analyse doit être faite dans le domaine fréquentiel, où le problèmeest plus facile à comprendre. La figure 17-5a est le signal produit par le détecteur(quelque chose que nous connaissons). La figure (c) représente le signal que nous souhaitons obtenir (ce que nous savons également). Cette impulsion souhaitée a été choisie arbitrairement pour avoir la même forme qu’une fenêtre de Blackman, avec une longueur d’environ un tiers de celle de l’impulsion originale. Notre objectif est de trouver un noyau de filtre (e) qui, lorsqu’il est convolué avec le signal de (a), produit le signal de (c). Sous forme d’équation : si a * e = c, et étant donné a et c, finde.
Si ces signaux étaient combinés par addition ou multiplication au lieu de la convolution, la solution serait facile : on utilise la soustraction pour « désadditionner » et la division pour « démultiplier ». La convolution est différente ; il n’existe pas d’opération inverse simple que l’on pourrait appeler « déconvolution ». La convolution est trop désordonnée pour être annulée en manipulant directement les signaux du domaine temporel.
Heureusement, ce problème est plus simple dans le domaine fréquentiel. Rappelez-vous,la convolution dans un domaine correspond à une multiplication dans l’autre domaine. En vous référant à nouveau aux signaux de la figure 17-5 : si b × f = d, et étant donné b et d, trouvez f. C’est un problème facile à résoudre : la réponse en fréquence du filtre, (f), est le spectre de fréquence de l’impulsion désirée, (d), divisé par le spectre de fréquence de l’impulsion détectée, (b). Comme l’impulsion détectée est asymétrique, elle aura une phase non nulle. Cela signifie qu’une division complexe doit être utilisée (c’est-à-dire une magnitude & phase divisée par une autre magnitude & phase). Au cas où vous l’auriez oublié, le chapitre 9 définit comment effectuer une division complexe d’un spectre par un autre. Le noyau de filtre requis, (e), est ensuite trouvé à partir de la réponse en fréquence par la méthode de filtre personnalisée (IDFT, décalage, troncature, &multiplication par une fenêtre).
Il y a des limites à l’amélioration que la déconvolution peut fournir. En d’autres termes, si vous devenez gourmand, les choses vont s’effondrer. Dans cet exemple, cela signifie que l’on essaie de rendre l’impulsion désirée excessivement étroite. Voyons ce qui se passe. Si l’impulsion souhaitée est rendue plus étroite, son spectre de fréquence doit contenir davantage de composantes haute fréquence. Comme ces composantes de haute fréquence sont de très faible amplitude dans l’impulsion détectée, le filtre doit avoir un gain très élevé à ces fréquences. Par exemple, (f) montre que certaines fréquences doivent être multipliées par un facteur de trois pour obtenir l’impulsion souhaitée en (c). Si l’impulsion désirée est rendue plus étroite, le gain du filtre de déconvolution sera encore plus grand aux hautes fréquences.
Le problème est que les petites erreurs sont très impitoyables dans cette situation. Par exemple, si une certaine fréquence est amplifiée de 30, alors que seulement 28 est nécessaire, le signal déconvolutionné sera probablement un désordre. Lorsque la déconvolution est poussée à de plus hauts niveaux de performance, les caractéristiques de la convolution indésirable doivent être comprises avec une plus grande exactitude et précision. Il y a toujours des inconnues dans les applications du monde réel, causées par des méchants tels que : le bruit électronique, la dérive de température, la variation entre les dispositifs, etc. Ces inconnues fixent une limite sur la façon dont la déconvolution fonctionnera.
Même si la convolution indésirable est parfaitement comprise, il y a toujours un factorth qui limite les performances de la déconvolution : le bruit. Par exemple, la plupart des convolutions non désirées prennent la forme d’un filtre passe-bas, réduisant l’amplitude des composantes haute fréquence du signal. La déconvolution corrige cela en amplifiant ces fréquences. Cependant, si l’amplitude de ces composantes tombe en dessous du bruit inhérent au système, les informations contenues dans ces fréquences sont perdues. Aucun traitement du signal ne peut les récupérer. Elle est perdue à jamais. Adios ! Goodbye ! Sayonara ! Essayer de récupérer ces données ne fera qu’amplifier le bruit. Dans un cas extrême, l’amplitude de certaines fréquences peut être complètement réduite à zéro. Cela ne fait pas qu’oblitérer l’information, mais cela va essayer de faire en sorte que le filtre de déconvolution ait un gain infini à ces fréquences. La solution : concevoir un filtre de déconvolution moins agressifet/ou placer des limites sur le gain autorisé à n’importe laquelle des fréquences.
Jusqu’où peut-on aller ? Jusqu’où peut-on être trop gourmand ? Cela dépend totalement duproblème que vous attaquez. Si le signal se comporte bien et a un faible bruit, une amélioration significative peut probablement être faite (pensez à un facteur de 5-10). Si le signal change au fil du temps, s’il n’est pas particulièrement bien compris ou s’il est bruité, vous ne ferez pas aussi bien (facteur 1 à 2). Une déconvolution réussie implique une grande quantité de tests. Si elle fonctionne à un certain niveau, essayez d’aller plus loin ; vous saurez quand elle s’effondrera. Aucune quantité de travail théorique ne vous permettra de contourner ce processus itératif.
La déconvolution peut également être appliquée aux signaux codés dans le domaine des fréquences. Un exemple classique est la restauration d’anciens enregistrements du célèbre chanteur d’opéra,Enrico Caruso (1873-1921). Ces enregistrements ont été réalisés avec un équipement très primitif par rapport aux normes modernes. Le problème le plus important est celui des résonances du long cornet d’enregistrement tubulaire utilisé pour recueillir le son. Chaque fois que le chanteur touche l’une de ces fréquences de résonance, le niveau sonore de l’enregistrement augmente brusquement. La déconvolution numérique a amélioré la qualité subjective de ces enregistrements en
réduisant les points forts de la musique. Nous ne décrirons que la méthode générale ; pour une description détaillée, voir l’article original : T. Stockham, T. Cannon, etR. Ingebretsen, « Blind Deconvolution Through Digital Signal Processing »,Proc. IEEE, vol. 63, Apr. 1975, pp. 678-692.
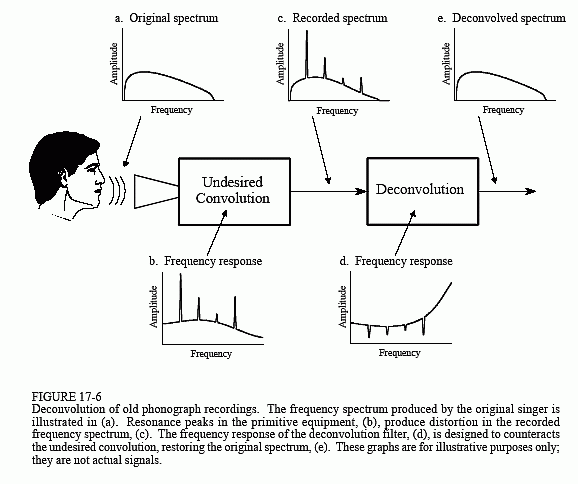
La figure 17-6 illustre l’approche générale. Le spectre de fréquence du signal audio original est illustré en (a). La figure (b) montre la réponse en fréquence de l’équipement d’enregistrement, une courbe relativement lisse à l’exception de plusieurs pics de résonance aigus. Le spectre du signal enregistré, illustré en (c), est égal au spectre réel, (a), multiplié par la réponse en fréquence irrégulière, (b). Le but de la déconvolution est de contrecarrer la déconvolution non désirée. En d’autres termes, la réponse en fréquence du filtre de déconvolution, (d), doit être l’inverse de (b). C’est-à-dire que chaque pic dans (b) est annulé par un creux correspondant dans (d). Si ce filtre était parfaitement conçu, le signal résultant aurait un spectre, (e), identique à celui de l’original.
Voilà le hic : l’équipement d’enregistrement original a été jeté depuis longtemps, et sa réponse en fréquence, (b), est un mystère. En d’autres termes, c’est un problème de déconvolution aveugle ; étant donné seulement (c), comment pouvons-nous déterminer (d) ?
Les problèmes de déconvolution aveugle sont généralement attaqués en faisant une estimation ou une hypothèse sur les paramètres inconnus. Pour traiter cet exemple, on suppose que le spectre moyen de la musique originale correspond au spectre moyen de la même musique interprétée par un chanteur actuel utilisant un équipement moderne. Le spectre moyen est trouvé par les techniques du chapitre 9 : décomposer le signal en un grand nombre de segments, prendre la TFD de chaque segment, convertir en forme polaire, puis faire la moyenne des amplitudes. Dans le cas le plus simple, la réponse en fréquence inconnue est considérée comme le spectre moyen de l’ancien enregistrement, divisé par le spectre moyen de l’enregistrement moderne. (La méthode utilisée par Stockham et al. est basée sur une technique plus sophistiquée appelée traitement homomorphique, fournissant une meilleure estimation descaractéristiques du système d’enregistrement).