Zéro est un nombre qui se situe carrément entre les nombres positifs et négatifs sur la ligne des nombres. Zéro est considéré comme un nombre entier, au même titre que les nombres naturels positifs (1, 2, 3, 4…) et les nombres négatifs, (…-4,-3,-2,-1).

Zéro est un nombre spécial dans les nombres entiers car c’est le seul nombre entier qui n’est ni positif ni négatif. C’est aussi le seul nombre entier qui n’est ni un nombre premier ni un nombre composé. Il est considéré comme un nombre pair car il est divisible par 2 sans reste. Zéro est l’élément d’identité additif dans divers systèmes d’algèbre, et le chiffre « 0 » est utilisé comme valeur de remplacement dans les systèmes de notation positionnelle pour représenter les nombres.

Zéro possède de nombreuses propriétés intéressantes qui le rendent intéressant pour les mathématiciens. Si vous ajoutez ou soustrayez zéro de n’importe quel nombre, le nombre reste le même Si vous multipliez 0 par n’importe quel nombre, le résultat est 0. Tout nombre élevé à la puissance zéro (0e) est égal à 1, donc 20=1 et 560=1. En algèbre traditionnelle, la division par 0 n’est pas définie, donc aucun nombre ne peut être divisé par 0. Le nombre 0 est également un élément des nombres réels et des nombres complexes.

Histoire du nombre 0

D’où vient l’idée du zéro ? De nos jours, elle nous semble intuitive ; le zéro est un nombre qui représente une quantité nulle – un rien. Nous voyons des zéros partout dans la société, et nous comprenons naturellement ce qu’ils signifient et comment ils peuvent être manipulés mathématiquement. Historiquement cependant, le concept de 0 a mis un certain temps à être universellement reconnu comme un objet des mathématiques, et beaucoup à travers l’histoire ont soutenu que le nombre zéro n’existe pas, ou que l’idée de zéro est un concept incohérent.

Plusieurs sociétés anciennes n’avaient pas un concept explicite de la quantité de zéro ou un chiffre spécifique à utiliser pour sa représentation. Les anciens Égyptiens et les Babyloniens avaient tous deux une certaine idée d’une quantité nulle et un besoin de valeurs de remplacement dans la représentation des nombres, mais ils n’ont jamais développé un chiffre ou un concept distinct pour représenter cette quantité ou cette valeur de remplacement. Les systèmes de numération de l’Égypte ancienne étaient entièrement picturaux et n’avaient pas de valeurs de position, tandis que les Babyloniens anciens utilisaient des espaces entre les chiffres pour représenter les valeurs de position.

Les Mayas avaient bien un concept explicite de 0 et avaient un chiffre distinct pour représenter le concept et l’utiliser comme valeur de placeholder dans leur système de calendrier vigésimal (base-20). Si les sociétés mayas, olmèques et autres sociétés précolombiennes ont été parmi les premières de l’histoire à avoir une compréhension explicite et sophistiquée du nombre 0, ces systèmes n’ont pas continué à influencer les sociétés de l’Ancien Monde en Europe.

Les Grecs anciens, en revanche, avaient une relation compliquée avec le zéro. Ils n’avaient pas de symbole pour son concept ou pour le considérer comme une valeur de remplacement, car ils n’étaient pas sûrs que le nombre 0 puisse être considéré comme une véritable chose existante. Comment, demandaient-ils, quelque chose (un nombre) peut-il être rien (zéro) ? Pour les Grecs, les nombres naturels (1, 2, 3, 4,…) étaient dérivés de notre compréhension des objets individuels discrets dans le monde. Aristote lui-même a soutenu que 0 n’existait pas, au motif que 0 représente un vide ou un néant, et qu’un vide ou un néant authentique ne peut pas exister.

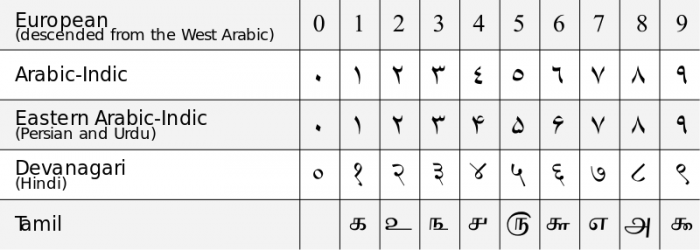
Les Chinois avaient une compréhension de « 0 » comme chiffre de remplacement pour leurs systèmes de comptage, mais ils ne considéraient pas le chiffre « 0 » comme représentant un nombre distinct, seulement un symbole utile. La compréhension commune du « 0 » comme un nombre distinct et comme un chiffre pour les systèmes de notation positionnelle est venue de l’Inde au cours du 6e siècle de notre ère. Les mathématiciens indiens de l’époque ont développé les premiers types de systèmes de notation décimale (base 10) qui incorporaient le 0 comme chiffre distinct et comprenaient les propriétés mathématiques uniques du zéro. Au 11e siècle de notre ère, l’idée du zéro s’est répandue en Europe occidentale sous l’influence de mathématiciens islamiques vivant en Espagne sous le califat des Omeyyades, et le système moderne de notation décimale en chiffres arabes a été créé. La première utilisation du mot anglais « zero » remonte à 1589.

Propriétés mathématiques du zéro

Le nombre zéro joue un rôle intégral dans presque tous les domaines des mathématiques. Zéro est le plus petit entier non négatif et n’a aucun nombre naturel qui le précède. Puisque 0 est un nombre entier, c’est aussi un nombre rationnel, un nombre réel et un nombre complexe. En mathématiques, 0 est considéré comme une quantité qui correspond à une quantité nulle. On pourrait dire que zéro est la « quantité » possédée par un ensemble qui n’a pas de membres.

En algèbre

En algèbre élémentaire, le zéro est souvent exprimé comme étant situé au centre de la ligne des nombres. Le nombre 0 est considéré comme un nombre pair car il est un multiple entier du nombre 2 (2×0=0). 0 n’est pas un nombre premier car il a une quantité infinie de facteurs, et il n’est pas un nombre composite car aucun produit de deux nombres premiers n’est égal au nombre 0.

Par rapport aux 4 principaux opérateurs arithmétiques (+, -, ×, ÷) et à l’opération de l’exposant, le nombre 0 se comporte selon les règles suivantes :

• Addition : x+0=0+x=x. Le zéro est considéré comme l’élément d’identité additif car tout nombre plus ou moins zéro est égal à ce nombre
• Soustraction : x-0=x et 0-x=-x
• Multiplication : x⋅0=0⋅x=0. Tout nombre fois 0 est aussi égal à 0.
• Division : 0/x=0, sauf quand x=0. x/0 est une quantité mathématiquement indéfinie, car 0 n’a pas d’inverse multiplicatif (aucun nombre multiplié par 0 ne donne 1).
• Exposés : x0=1, sauf quand x=0. Il y a longtemps eu un débat pour savoir si 00 est indéfini ou une expression bien formée. Pour tout x positif, 0x=0.

Dans les expressions impliquant des limites, la quantité 0/0 peut surgir dans le contexte de la démonstration des limites de fonctions rationnelles comme f(x)/g(x). Dans ces cas, 0/0 n’est pas indéfini mais représente une forme indéterminée. Cela ne signifie pas que la limite est indéfinie mais qu’elle doit être calculée par une autre méthode, telle que la recherche de dérivées. Il existe bien quelques modèles algébriques où la division par zéro donne une quantité définie, comme la ligne réelle étendue de manière projective ou la sphère de Riemann.

En théorie des ensembles

En théorie des ensembles, le nombre 0 correspond à la cardinalité l' »ensemble vide » ou l' »ensemble nul » (couramment représenté par {} ou {∅}. La cardinalité d’un ensemble est la quantité d’éléments dans cet ensemble si l’on n’a pas d’oranges, alors on a un ensemble de 0 oranges (un ensemble vide d’oranges).

Zéro est souvent utilisé comme point de départ en théorie des ensembles pour construire le reste des nombres naturels. Ces constructions de von Neumman, du nom du célèbre polymathe John von Neumann construit les nombres naturels en définissant 0={} et définit une fonction successeur S(a) = a ∪ {a}. L’intégralité des nombres naturels peut être construite à partir des applications récursives de la fonction successeur en commençant par l’ensemble vide :

0 = {}

1 = 0 ∪ {0} = {0} = {{}}

2 = 1 ∪ {1} = {0,1} = {{}, {{}}}

3 = 2 ∪ {2} = {0, 1, 2} = {{}, {{}}, {{}, {{}}}}

et ainsi de suite. En suivant ce schéma, on peut construire l’ensemble infini des nombres naturels. De cette façon, on peut dire que chaque nombre naturel correspond à l’ensemble contenant tous les nombres naturels qui le précèdent.

En physique

Dans le contexte de la réalisation de mesures quantitatives en physique, 0 est considéré comme la ligne de base à partir de laquelle toutes les autres mesures d’unités sont effectuées. Très souvent, la ligne de base de 0 correspond à une certaine variable physiquement significative qui se distingue naturellement de toutes les autres grandeurs de mesure.

Par exemple, dans l’échelle Kelvin, une température de 0 K correspond au 0 absolu- la température la plus froide qui est physiquement possible. Dans l’échelle de température Celsius, 0 °C est défini comme le point de congélation de l’eau aux pressions atmosphériques. Dans le contexte de la dynamique et de l’électromagnétisme, la valeur 0 est attribuée à la position dans laquelle un système possède la quantité minimale possible d’énergie potentielle. Par exemple, l’état fondamental d’un atome, le niveau d’énergie le plus bas possible pour les électrons de l’atome, se voit souvent attribuer la valeur 0.

De même, dans le contexte de la cinématique, le cadre de référence à partir duquel les observations du mouvement sont faites est défini comme ayant un point central posé sur l’origine de l’axe des coordonnées au point (0, 0). Dans le cas des quantités conservées, comme la masse-énergie, la quantité de mouvement et le moment angulaire, la quantité totale de changement des quantités conservées dans un système isolé est toujours égale à 0.

En informatique

Les ordinateurs stockent les informations sous la forme de séquences de 1 et de 0, longues de plusieurs bits. Dans cette représentation binaire, 0 correspond à une position « off » et s’oppose à la position « on » désignée par 1. Une valeur de 0 sur un circuit électrique signifie que le circuit est éteint et n’a pas de flux électrique. De même, de nombreuses logiques de calcul définissent le « 0 » comme le caractère qui représente une fausse valeur de vérité.

Dans les bases de données informatiques, les éléments d’un tableau sont comptés en utilisant un système de comptage basé sur le zéro. Cela signifie que pour un ensemble de n éléments, les éléments ont des indices commençant par 0. Ainsi, un élément dont le numéro d’indice est 0 est en fait le premier élément de la série, et un numéro d’indice de 1 correspond au deuxième élément, et ainsi de suite. En général, le nième terme d’un ensemble a un numéro d’indice correspondant à n-1. Ce système de comptage peut être source de confusion pour les nouveaux programmeurs qui ont l’habitude d’attribuer intuitivement des valeurs d’indice commençant par 1.