Qu’est-ce que la forme d’interception de pente

La forme d’interception de pente est l’une des trois formes que nous pouvons utiliser pour exprimer une ligne droite. Les autres formes sont appelées forme de la pente du point et forme standard, mais nous utiliserons principalement la forme de l’interception de la pente dans cette section. En utilisant la forme d’interception de pente, nous exprimons l’équation d’une droite comme étant :

y=mx+by = mx + by=mx+b

Vous connaissez peut-être xxx et yyy pour être les coordonnées d’un point sur un graphique, mais que sont mmm et bbb?

Que représente b dans y=mx+b?

La lettre b est un nombre qui représente le moment où la droite touche l’axe des y. On parle aussi de « l’ordonnée à l’origine ». Par exemple, traçons une ligne droite sur le plan de coordonnées.

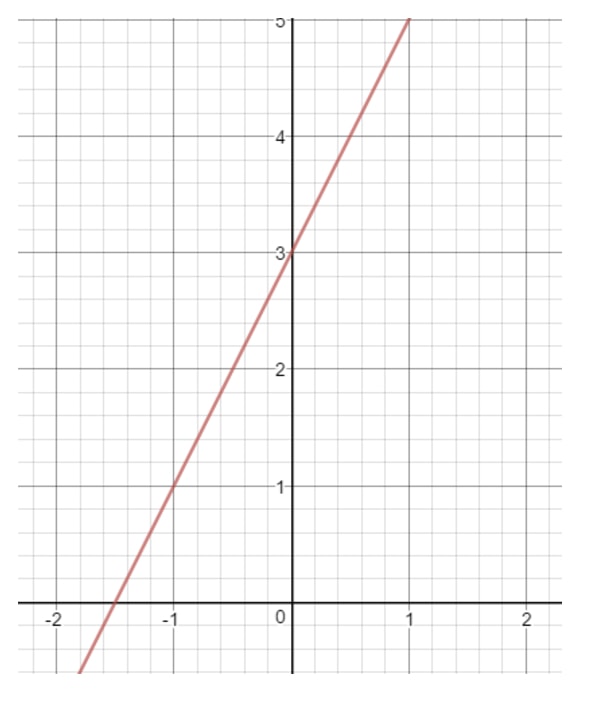
Si vous regardiez attentivement l’axe des y, la ligne droite touche l’axe des y à un endroit précis. Où est cet endroit ? Ce serait le nombre 3, car c’est là que l’axe des y et la ligne se croisent. On peut donc en conclure que b = 3.

Qu’est-ce que m sous forme d’interception de pente ?

La lettre m est un nombre qui représente la pente de la ligne. Certaines personnes font référence à la pente comme à la montée sur la descente. Rappelez-vous que si nous avons deux points, alors nous sommes en mesure de trouver la pente des deux points en utilisant la formule de la pente

m=riserun=y2-y1x2-x1m = \frac{rise}{run} = \frac{y_{2}. – y_{1}}{x_{2} – x_{1}}m=runrise=x2-x1y2-y1

La même idée fonctionne ici. Si nous prenons deux points quelconques sur une ligne droite, alors nous pouvons trouver la pente de la ligne en utilisant la formule ci-dessus ! Par exemple, utilisons cette ligne.

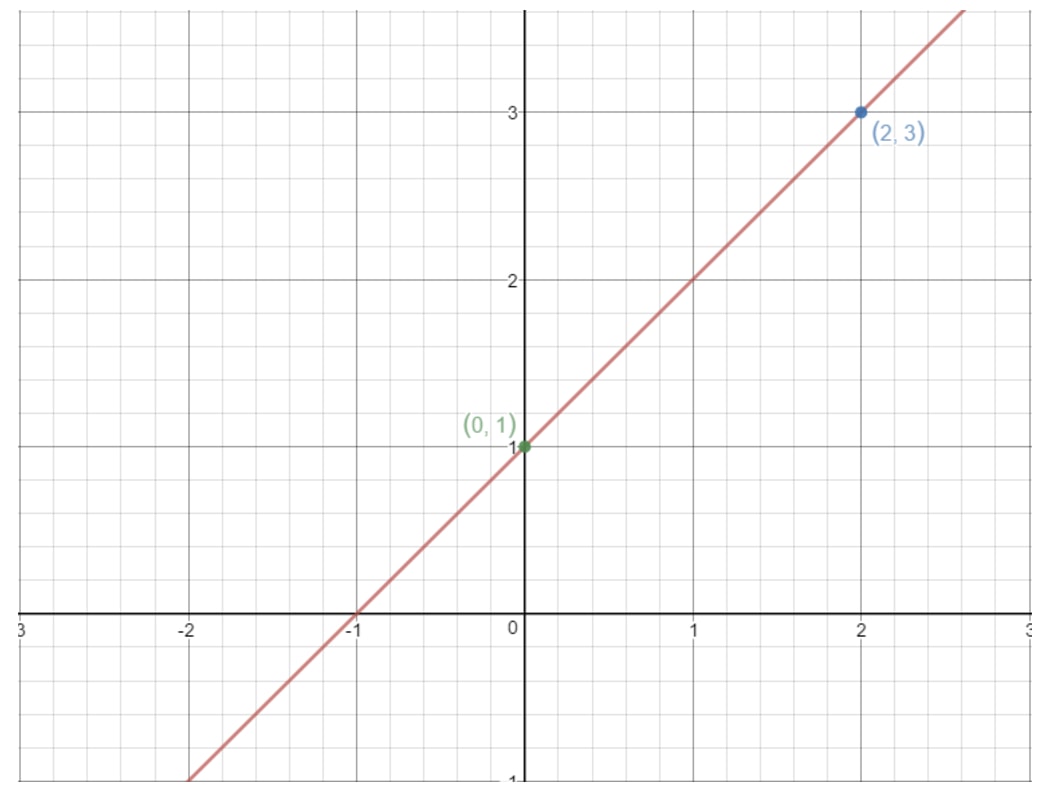
Notez que les points (2, 3) et (0, 1) sont sur ce graphique. Alors pourquoi n’utilisons-nous pas ces deux points pour trouver la pente de la ligne ? En utilisant la formule, nous obtiendrions :

m=y2-y1x2-x1=1-30-2m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}} = \frac{1 – 3}{0 – 2}m=x2-x1y2-y1=0-21-3=-2-2= \frac{-2}{-2}=-2-2=1= 1=1

Ce qui signifie que la pente de cette ligne est 111!

La particularité des pentes est que nous pouvons utiliser deux points quelconques de la ligne pour la trouver. Donc, si vous preniez deux points différents sur cette ligne, vous obtiendriez toujours que la pente est 111.

Comment écrire une équation sous forme d’interception de pente ?

Vous savez peut-être à quoi ressemble la forme d’interception de pente, mais la moitié du temps, on vous donnera des équations qui ne sont pas sous cette forme. C’est donc à vous de la transformer en forme d’interception de pente. Comment s’y prendre ? L’objectif est de toujours isoler le terme yyy. Par exemple, disons que l’on vous donne l’équation

6x+4+2y=06x + 4 + 2y = 06x+4+2y=0

Pour isoler yyy, nous déplaçons le 6x+46x + 46x+4 vers le côté droit de l’équation

2y=-6x-42y = -6x – 42y=-6x-4

Maintenant le 222 fait obstacle à yyy, nous allons donc nous en débarrasser en divisant les deux côtés de l’équation par 222.

2y2=-6x-42\frac{2y}{2} = \frac{-6x – 4}{2}22y=2-6x-4y=-6×2-42y = -\frac{6x}{2} – \frac{4}{2}y=-26x-24y=-3x-2y = -3x – 2y=-3x-2

Puisque yyy est isolé, vous pouvez voir qu’il est sous la forme pente intercept y=mx+by = mx + by=mx+b où m=-3m = -3m=-3, et b=-2b = -2b=-2.

Maintenant que nous connaissons très bien l’ordonnée à l’origine et la pente des y, pourquoi ne pas examiner des questions spécifiques pour les trouver !

Comment trouver l’ordonnée à l’origine de y ?

Question 1 : En utilisant l’équation linéaire y=12x+5y = \frac{1}{2} x + 5y=21x+5, trouvez l’ordonnée à l’origine de y.

Notez ici que l’équation est déjà sous la forme ordonnée à l’origine de la pente y=mx+by = mx + by=mx+b. Nous avons juste besoin de trouver ce que bbb est. Nous pouvons voir que b=5b = 5b=5, donc l’ordonnée à l’origine est 555.

Faisons une question un peu plus difficile.

Question 2 : Déterminer l’ordonnée à l’origine de 2x-4y=82x – 4y = 82x-4y=8

Maintenant, cette équation linéaire n’est pas sous la forme pente-ordonnée, donc nous devons d’abord la changer sous cette forme. Notre objectif est d’isoler yyy dans cette équation.

Voyez que si nous déplaçons le 2x2x2x vers le côté droit de l’équation, nous aurons :

-4y=8-2x-4y = 8 – 2x-4y=8-2x

Maintenant en divisant les deux côtés par -4-4-4, nous obtiendrons :

-4y-4=8-2x-4\frac{-4y}{-4} = \frac{8 – 2x}{-4}-4y=-48-2xy=8-4-2x-4y = \frac{8}{-4} – \frac{2x}{-4}y=-48–42xy=-2+12xy = -2 + \frac{1}{2}xy=-2+21x

En permutant maintenant les positions des deux termes, on obtient :

y=12x-2y = \frac{1}{2}x – 2y=21x-2

Question 3 : Déterminez l’ordonnée à l’origine de 4y-8=04y – 8 = 04y-8=0.

Cela peut paraître un peu bizarre car il n’y a pas de terme xxx, mais notre objectif reste le même. Nous allons isoler yyy.

En déplaçant le -8-8-8 vers le côté droit de l’équation, on obtient :

4y=84y = 84y=8

Diviser les deux côtés de l’équation par 444 nous donne

4y4=84\frac{4y}{4} = \frac{8}{4}44y=48y=2y = 2y=2

Maintenant, cela n’en a peut-être pas l’air, mais l’équation est sous forme d’interception de pente. C’est juste que m=0m = 0m=0, donc le terme mxmxmx entier a disparu. Il suffit de réécrire l’équation comme

y=0m+2y = 0m + 2y=0m+2

En observant, vous pouvez dire que b=2b = 2b=2, et donc que l’ordonnée à l’origine est 222. Faisons une autre question.

Question 4 : Déterminez (si possible) l’ordonnée à l’origine de 5x-15=05x – 15 = 05x-15=0.

Cette question est intéressante car l’équation n’a pas de terme yyy. Alors comment sommes-nous censés la mettre sous forme d’ordonnée à l’origine ? Eh bien, la seule chose que nous pouvons faire maintenant est d’isoler pour xxx, alors essayons cela pour le moment.

En déplaçant le 151515 vers le côté droit de l’équation, nous avons:

5x=155x = 155x=15

En divisant les deux côtés de l’équation, on obtient :

5×5=155\frac{5x}{5} = \frac{15}{5}55x=515x=3x = 3x=3

Maintenant nous allons dessiner ceci sur un graphique. Remarquez que dans cette équation, xxx est forcé d’être 333 et ne peut pas être autre chose. Cependant, elle ne dit rien sur yyy, donc yyy peut être ce qu’elle veut. Si nous devions écrire un tableau de valeurs, nous obtenons :

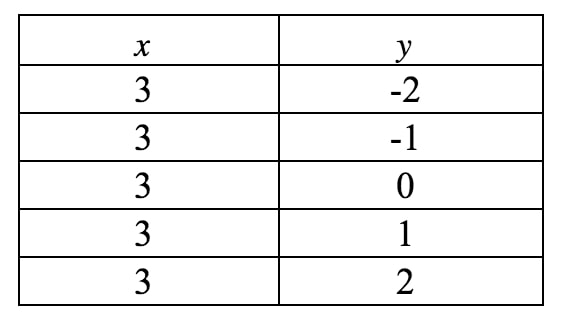
Si nous traçons ces points sur un plan de coordonnées et traçons la ligne, nous avons :

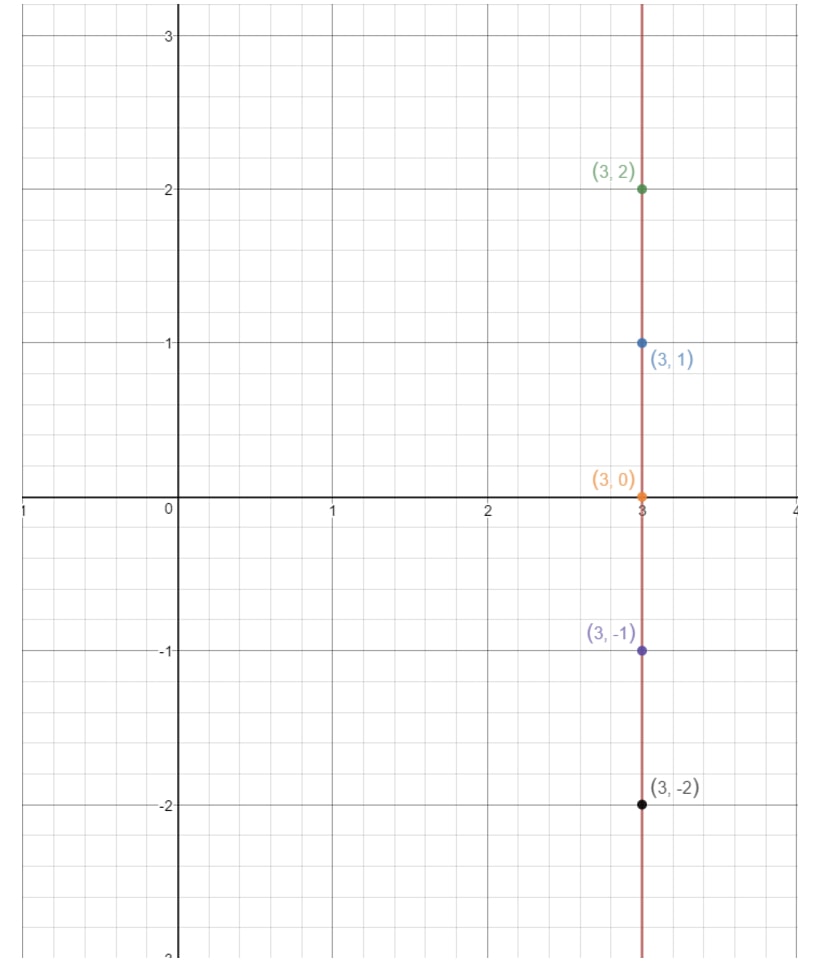
Notez comment la ligne ne touche jamais l’axe des y. Cela signifie que l’équation n’a pas d’ordonnée à l’origine. Maintenant que nous avons couvert tous les cas de recherche de l’ordonnée, examinons les questions qui nous demandent de trouver la pente!

Comment trouver la pente d’une équation ?

Question 5 : Trouver la pente de y=32x+1y = \frac{3}{2}x + 1y=23x+1

Question 6 : Déterminer la pente de l’équation linéaire 6x-6y=06x – 6y = 06x-6y=0

Comme vous pouvez le voir, l’équation n’est pas sous forme d’ordonnée à l’origine, nous devons donc d’abord la convertir sous cette forme. Notre objectif est d’isoler yyy.

En déplaçant 6x6x6x vers le côté droit de l’équation, on obtient :

-6y=-6x-6y = -6x-6y=-6x

En divisant les deux côtés par -6-6-6, on obtient :

-6y-6=-6x-6\frac{-6y}{-6} = \frac{-6x}{-6}-6-6y=-6-6xy=xy = xy=x

Notez que c’est en fait sous la forme pente-interception y=mx+by = mx + by=mx+b. C’est juste que l’ordonnée à l’origine bbb dans ce cas est 000, et xxx est la même chose que 1x1x1x. Nous pouvons donc réécrire l’équation en:

y=1x+0y = 1x + 0y=1x+0

Maintenant en observant, nous voyons que m=1m = 1m=1. Puisque mmm est la pente, alors la pente doit être de 111. Faisons-en une un peu plus difficile

Question 7 : Déterminer la pente de 2y-4=02y – 4 = 02y-4=0

Encore, c’est un peu bizarre car nous n’avons pas de terme xxx. Cependant, notre objectif d’isoler yyy reste le même.

En déplaçant -4-4-4 vers le côté droit de l’équation, nous avons :

2y=42y = 42y=4

Diviser les deux côtés de l’équation par 222 donne :

2y2=42\frac{2y}{2} = \frac{4}{2}22y=24y=2y = 2y=2

Voyez ici que c’est maintenant sous la forme pente intercept, sauf que le terme mxmxmx est caché car m=0m = 0m=0. Nous pouvons donc réécrire notre équation comme suit :

y=0x+2y = 0x + 2y=0x+2

Puisque m=0m = 0m=0, alors nous avons une pente nulle. Si vous vous demandez à quoi ressemble une ligne avec 000 de pente, alors voici un graphique pour que vous puissiez le voir.

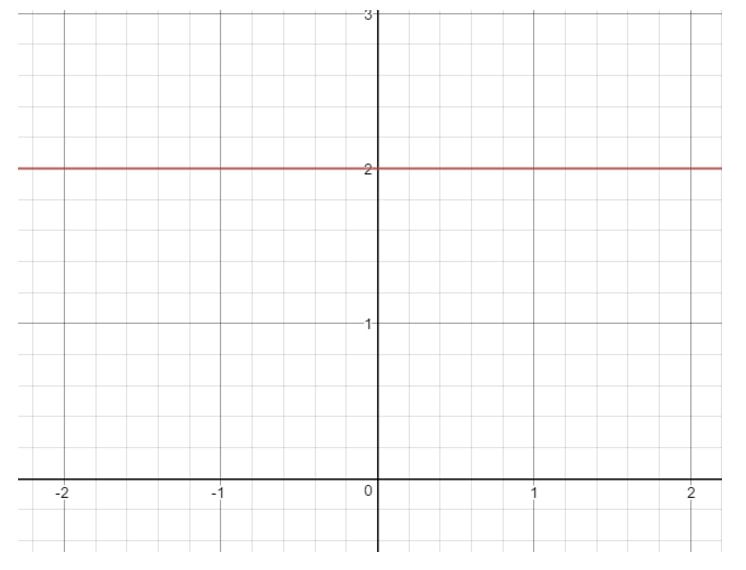
Question 8 : Trouvez (si possible) la pente de l’équation linéaire 16-4x=016 – 4x = 016-4x=0

Dans ce cas, yyy ne peut pas être isolé car il n’y a pas de terme yyy. La seule chose que l’on puisse faire est donc d’isoler xxx.

En déplaçant 161616 à droite de l’équation, on obtient :

-4x=-16-4x = -16-4x=-16

En divisant les deux côtés par -4-4-4, on obtient :

-4x-4=-16-4\frac{-4x}{-4} = \frac{-16}{-4}-4-4x=-4-16x=4x = 4x=4

Ceci n’est toujours pas sous forme d’intercept de pente, donc notre seul espoir d’atteindre la pente est de dessiner un graphique de cette ligne. Encore une fois, nous voyons que xxx est toujours forcé d’être 444, mais que yyy peut être ce qu’il veut car il n’y a pas de terme yyy. Si nous devions écrire un tableau de valeurs, nous obtenons :

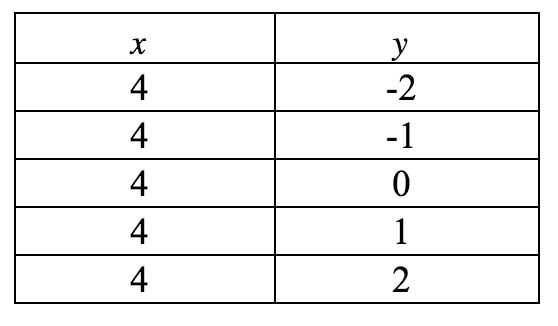
Si nous reportons ces points sur un plan de coordonnées et traçons la droite, nous avons :

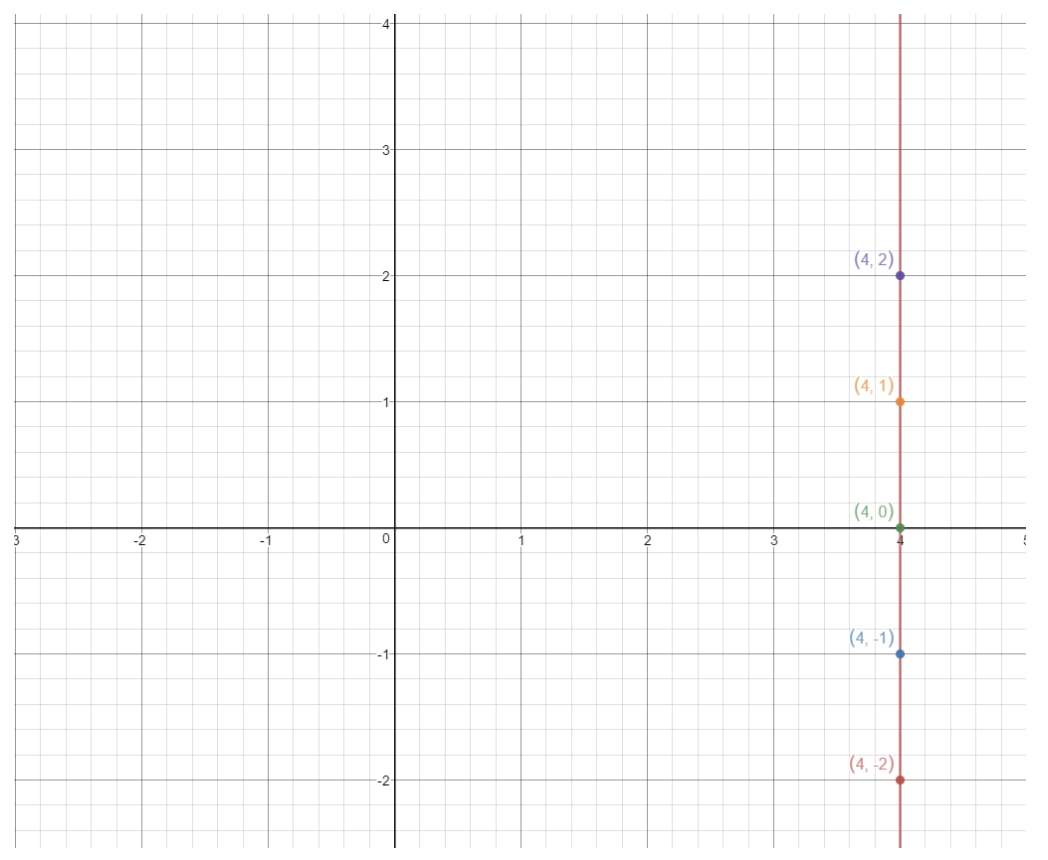
C’est une ligne verticale. Alors, quelle est la pente d’une ligne verticale ? Essayons de le savoir en trouvant la montée et la descente. Voyez comment cette ligne monte toujours à l’infini, mais il n’y a pas de course du tout. Cela signifie donc que la course est de 000. Donc si nous calculons la pente, alors nous obtiendrons :

m=riserun=rise0=undefinedm = \frac{rise}{run} = \frac{rise}{0} = undefinedm=runrise=0rise=undefined

Nous ne pouvons pas diviser par 000, donc nous avons en fait une pente indéfinie.

Qu’est-ce qu’une pente indéfinie ?

Une pente indéfinie est une pente qui monte directement dans le graphique. Comme on le voit dans le graphique ci-dessus, la pente monte infiniment et n’a pas de course. Par conséquent, nous obtenons une pente indéfinie parce que nous ne pouvons pas diviser par 000.

En général, nous obtenons toujours une pente indéfinie chaque fois que nous obtenons une ligne verticale droite !

Regardons d’autres questions uniques !

Détermination d’une équation à partir d’un point

Question 9 : Un point (2, 6) passe par une équation de y=-5x+by = -5x + by=-5x+b. Trouvez « bbb ».

6=-5(2)+b6 = -5(2) + b6=-5(2)+b

En isolant et en résolvant bbb, on obtient :

6=-10+b6 = -10 + b6=-10+bb=16b = 16b=16

Rappellez-vous que bbb est aussi connu comme l’ordonnée à l’origine, donc l’ordonnée à l’origine est aussi 161616 !

Détermination de la pente à partir de deux points

Question 10 : Étant donné deux points (6, 1) et (-10, 9), trouvez la pente de la droite.

Rappellez que pour trouver la pente de la droite, nous utilisons l’équation de la pente

m=y2-y1x2-x1m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}m=x2-x1y2-y1

L’utilisation de cette formule nous donne donc :

m=9-1-10-6=8-16m = \frac{9 – 1}{-10 – 6} = \frac{8}{-16}m=-10-69-1=-168=1-2= \frac{1}{-2}=-21

Et si on est censé trouver l’équation entière d’une ligne à la place ?

Équation d’une droite étant donné deux points

Question 11 : Étant donné deux points (-6, 1) et (2, 6), trouvez l’équation sous forme d’intercept de pente.

Nous essayons essentiellement de trouver l’équation sous la forme y=mx+by = mx + by=mx+b. Pour ce faire, nous devons chercher mmm et bbb.

Rappelons que pour trouver mmm, nous utilisons l’équation de la pente

m=y2-y1x2-x1m = \frac{y_{2}}. – y_{1}}{x_{2} – x_{1}}m=x2-x1y2-y1

L’utilisation de cette formule nous donne donc :

m=6-12-(-6)=58m = \frac{6 – 1}{2 – (-6)} = \frac{5}{8}m=2-(-6)6-1=8558\frac{5}{8}85

Nous avons donc maintenant l’équation

y=58x+by = \frac{5}{8}x + by=85x+b

Nous devons maintenant chercher bbb. Pour résoudre bbb, on choisit l’un ou l’autre des points donnés et on l’intègre dans l’équation. Nous pouvons le faire parce que les deux points se trouvent sur la ligne, et que n’importe quel point de la ligne satisferait l’équation. Utilisons le point (2, 6). Voyez que:

6=58(2)+b6 = \frac{5}{8}(2) + b6=85(2)+b

Isoler bbb donne:

6=108+b6 = \frac{10}{8} + b6=810+bb=6-108b = 6 – \frac{10}{8}b=6-810b=488-108b = \frac{48}{8} – \frac{10}{8}b=848-810b=388b = \frac{38}{8}b=838

En mettant cela sous forme décimale, nous obtenons que b=4.75b = 4.75b=4.75. Par conséquent, notre équation sous forme d’interception de pente est :

y=58x+4.75y = \frac{5}{8}x + 4.75y=85x+4.75

La dernière chose à couvrir dans cette section est de trouver le domaine et l’étendue d’une ligne.

Comment trouver le domaine et l’étendue ?

Pour trouver le domaine d’une ligne, nous nous posons essentiellement cette question : que peut être xxx ? Si xxx peut être ces valeurs, alors nous les ajoutons dans le domaine.

C’est la même chose pour l’étendue. Que peut être yyy ? Si yyy peut être ces valeurs, alors nous les ajoutons dans la gamme. Faisons un exemple.

Question 12 : Trouvez le domaine et l’étendue de l’équation y=2x+1y = 2x + 1y=2x+1.

Notez que si nous dessinons le graphique de cette ligne, alors nous obtiendrons :

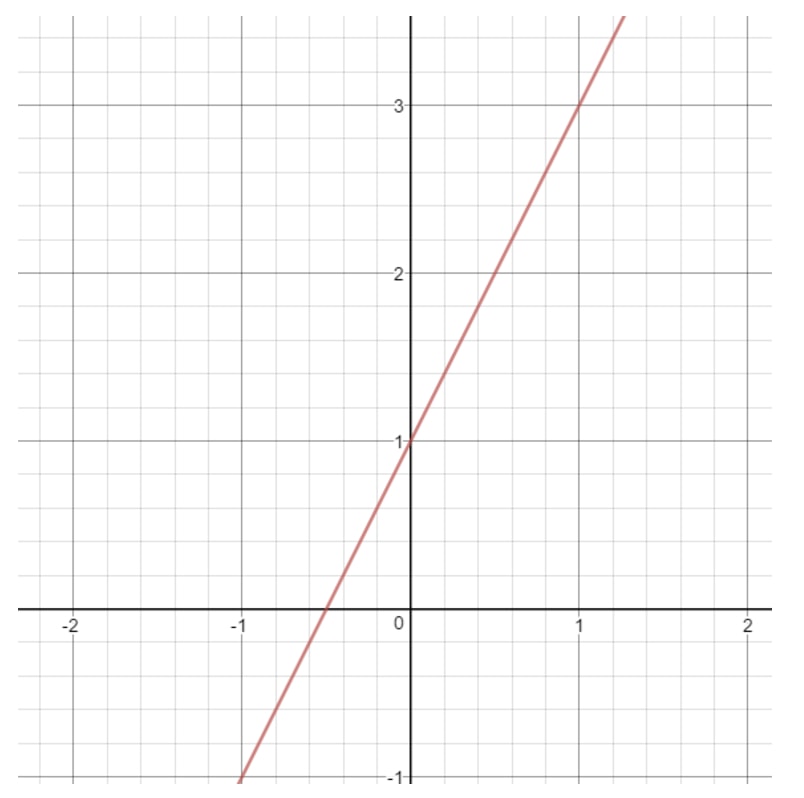
Que peut être xxx dans cette ligne ? Remarquez que xxx peut être n’importe quoi car avec n’importe quelle valeur de xxx, nous pouvons obtenir un point qui est sur la ligne. Il en va de même pour y. Nous pouvons toujours choisir une valeur yyy qui nous donne un point sur une ligne. Donc on dit que

Domaine : {x∈\in∈R}Etendue : {y∈\in∈R}

où R signifie « tous les nombres réels ». Faisons une question plus difficile.

Question 13 : Trouvez le domaine et l’étendue de l’équation y=-2y = -2y=-2.

Maintenant, si nous traçons cette ligne sur un graphique, nous obtiendrons :

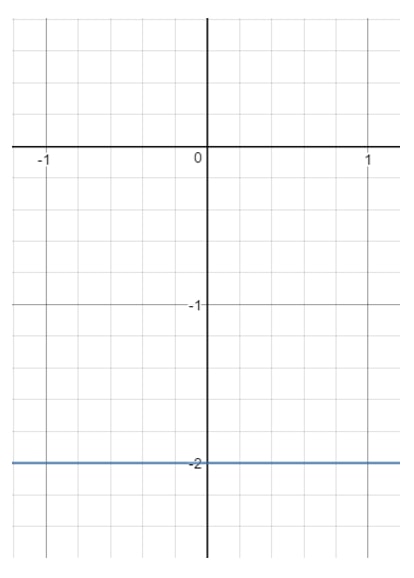
Notez que xxx peut être n’importe quoi car avec n’importe quelle valeur de xxx, nous pouvons obtenir un point qui est sur la ligne tant que y=-2y = -2y=-2. Cependant, regardez yyy. Vous voyez que yyy est forcé à -2-2-2 et ne peut pas être autre chose. Dès que vous choisissez une autre valeur de yyy (comme 111), ce point se trouve en dehors de la ligne. Cela signifie donc :

Domaine : {x ∈\in∈ R}Etendue : {y = -2}

Question 14 : Trouvez le domaine et l’étendue de l’équation x=1x = 1x=1.

Maintenant si nous traçons cette ligne sur un graphique, nous obtiendrons :

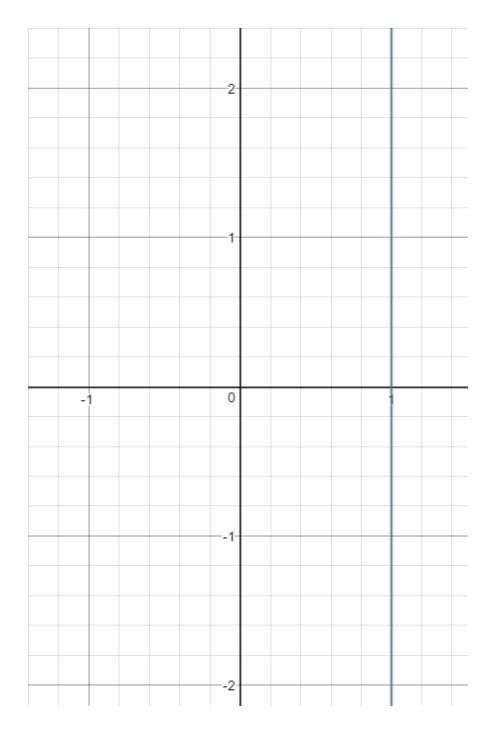
Vous voyez que xxx est forcé à 111 et ne peut pas être autre chose. Au moment où vous choisissez une autre valeur de xxx (comme 222), alors ce point va être hors de la ligne.Cependant, regardez yyy. Remarquez que yyy peut être n’importe quoi car avec n’importe quelle valeur de yyy, on peut obtenir un point qui est sur la ligne tant que x=1x = 1x=1

C’est donc :

Domaine : {x=1}Etendue : {y∈\in∈R}

Si vous avez eu beaucoup de problèmes à dessiner les graphiques pour obtenir le domaine et l’étendue, je vous recommande d’utiliser cette calculatrice.

https://www.desmos.com/calculator/2rnqgoa6a4

Elle vous apprend à tracer le graphique d’une équation linéaire. Tout ce que vous avez à faire est de taper les valeurs de mmm et bbb. Ensuite, il tracera automatiquement la ligne pour vous ! C’est également utile lorsque vous essayez de trouver la forme de l’intercept de la pente.