par Marco Taboga, PhD
La fonction indicatrice d’un événement est une variable aléatoire qui prend la valeur 1 lorsque l’événement se produit et la valeur 0 lorsque l’événement ne se produit pas. Les fonctions indicatrices sont souvent utilisées en théorie des probabilités pour simplifier la notation et prouver des théorèmes.
Définition
Ce qui suit est une définition formelle.
Définition Soit 
un espace échantillon et un événement. La fonction indicatrice (ou variable aléatoire indicatrice) de l’événement , notée , est une variable aléatoire définie comme suit :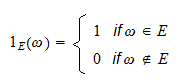
Alors que l’indicateur d’un événement est habituellement désigné par , il est parfois aussi désigné paroù est la lettre grecque Chi.
Exemple On lance un dé et l’un des six nombres de 1 à 6 peut apparaître face visible. L’espace d’échantillonnage estDéfinir l’événement décrit par la phrase « Un nombre pair apparaît face visible ». Une variable aléatoire qui prend la valeur 1 lorsqu’un nombre pair apparaît face visible et la valeur 0 sinon est un indicateur de l’événement . La définition au cas par cas de cet indicateur est
De la définition ci-dessus, on peut facilement voir que est une variable aléatoire discrète avec support et fonction de masse de probabilité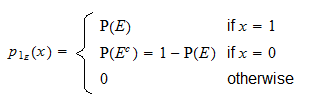
Propriétés
Les fonctions indicatrices jouissent des propriétés suivantes.
Puissances
La ième puissance de est égale à :parce que peut être soit soit et
Valeur attendue
La valeur attendue de est égale à :
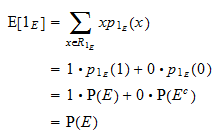
Variance
La variance de est égale à . Grâce à la formule de variance usuelle et à la propriété des puissances ci-dessus, on obtient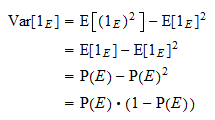
Intersections
Si et sont deux événements, alorsparce que :
-
si
, alors et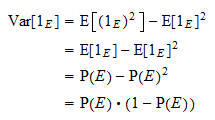
-
si
, alorset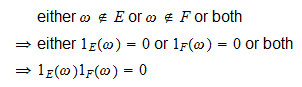
Indicateurs d’événements à probabilité nulle
Soit un événement à probabilité nulle et une variable aléatoire intégrable. Alors,Bien qu’une preuve rigoureuse de ce fait dépasse le cadre de cet exposé introductif, cette propriété devrait être intuitive. La variable aléatoire est égale à zéro pour tous les points de l’échantillon , sauf éventuellement pour les points . La valeur attendue est une moyenne pondérée des valeurs que peut prendre, où chaque valeur est pondérée par sa probabilité respective. Les valeurs non nulles que peut prendre sont pondérées par des probabilités nulles, donc doit être nulle.
Exercices résolus
Vous trouverez ci-dessous quelques exercices avec les solutions expliquées.
Exercice 1
Considérons une variable aléatoire et une autre variable aléatoire définie comme une fonction de .
Exprimez en utilisant les fonctions indicatrices des événements et .
Dénotez par l’indicateur de l’événement et dénotez par l’indicateur de l’événement . On peut écrire comme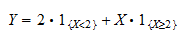
Exercice 2
Soit une variable aléatoire positive, c’est-à-dire une variable aléatoire qui ne peut prendre que des valeurs positives. Soit une constante. Prouvez que où est l’indicateur de l’événement .
Notez d’abord que la somme des indicateurs et est toujours égale à :En conséquence, on peut écrire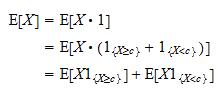
Notez ensuite que est une variable aléatoire positive et que la valeur espérée d’une variable aléatoire positive est positive :Donc,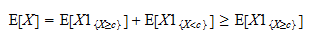
Exercice 3
Soit un événement et désignons sa fonction indicatrice par . Soit le complément de et on désigne sa fonction indicatrice par . Pouvez-vous exprimer comme une fonction de ?
La somme des deux indicateurs est toujours égale à :C’est pourquoi,
Comment citer
Veuillez citer comme:
Taboga, Marco (2017). « Fonctions indicatrices », Lectures sur la théorie des probabilités et la statistique mathématique, troisième édition. Kindle Direct Publishing. Annexe en ligne. https://www.statlect.com/fundamentals-of-probability/indicator-functions.