Lorsque la lumière est réfléchie ou transmise par une structure matérielle, il y a un changement de polarisation. L’ellipsométrie mesure cette réponse qui dépend des propriétés optiques et de l’épaisseur des matériaux individuels. L’ellipsométrie est principalement utilisée pour déterminer les constantes optiques et l’épaisseur des films, mais aussi pour caractériser la composition, la cristallinité, la rugosité, la concentration de dopage et d’autres propriétés du matériau associées à un changement de réponse optique.

Les domaines d’application sont la recherche fondamentale en sciences physiques, les solutions de semi-conducteurs et de stockage de données, les écrans plats, la communication, les biocapteurs et les industries de revêtement optique. L’ellipsométrie a également la flexibilité de mesurer la plupart des types de matériaux : diélectriques, semi-conducteurs, métaux, supraconducteurs, organiques, revêtements biologiques et composites.

Définition de la lumière polarisée

La lumière peut être décrite comme une onde électromagnétique se déplaçant dans l’espace. La façon dont le champ d’une onde électromagnétique se comporte par rapport à l’espace et au temps est appelée polarisation. La lumière est considérée comme non polarisée lorsque son orientation et sa phase sont totalement arbitraires. L’ellipsométrie, en revanche, mesure la lumière polarisée – un champ électrique qui suit une trajectoire spécifique et a une forme distincte en tout point. Une onde électromagnétique qui se propage dans la direction z peut être décrite par ses composantes x et y, car son champ électrique est toujours orthogonal à la direction de propagation. Lorsque deux ondes lumineuses orthogonales sont en phase, la lumière qui en résulte est polarisée linéairement. Son orientation est déterminée par les amplitudes relatives. La lumière est considérée comme polarisée circulairement si les ondes orthogonales sont déphasées de 90° et ont la même amplitude. La polarisation la plus courante est elliptique et combine des ondes orthogonales d’amplitude et de phase arbitraires. C’est de là que l’ellipsométrie tire son nom.

Différents types de polarisation:

Linéaire

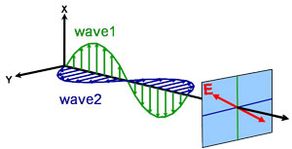
Circulaire

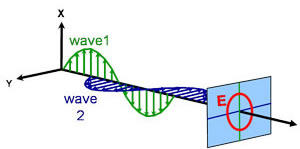
Elliptique

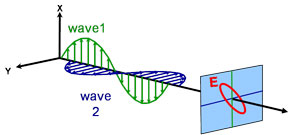
Propriétés optiques

Les propriétés optiques qui déterminent comment la lumière interagit avec un matériau sont décrites par deux valeurs. Elles sont généralement représentées par un nombre complexe. L’indice de réfraction complexe (ñ) se compose de l’indice (n) et d’un coefficient d’extinction (k):

Les propriétés optiques peuvent également être représentées comme une fonction diélectrique complexe:

avec la relation suivante entre les conventions :

L’indice représente la vitesse de phase de la lumière lorsqu’elle se déplace dans un matériau par rapport à la vitesse de la lumière lorsqu’elle se déplace dans le vide, c:

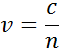
Lorsqu’elle pénètre dans un matériau avec un indice plus élevé, la lumière ralentit. Comme la fréquence des ondes lumineuses ne change pas, la longueur d’onde se raccourcit. La perte d’énergie des ondes dans le matériau est décrite par le coefficient d’extinction qui est lié au coefficient d’absorption de la manière suivante :

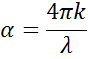
Selon la loi de Beer, la lumière perd de son intensité dans un matériau absorbant. Le coefficient d’extinction démontre à quelle vitesse la lumière disparaît dans un matériau.

La figure 4 montre une onde lumineuse voyageant à travers deux matériaux différents aux propriétés variables avant de retourner dans l’ambiance.

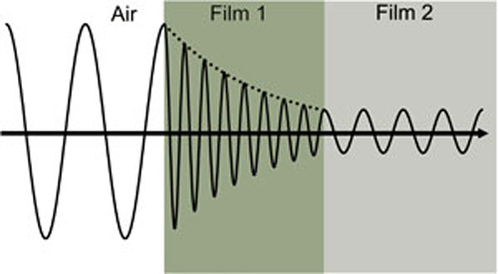
Figure 4 : onde lumineuse voyageant de l’air dans le film absorbant 1 puis dans le film transparent 2. La vitesse de phase et la longueur d’onde changent dans les deux matériaux en fonction de l’indice de réfraction (Film 1 : n=4, Film 2 : n=2).

La longueur d’onde détermine les constantes optiques. La figure 5 montre les constantes optiques du TiO2 de l’UV à l’IR. En raison des différents processus qui tirent l’énergie de l’onde lumineuse, l’absorption (k>0) se produit dans les UV et les IR. L’absorption dans l’IR est généralement causée par une vibration moléculaire ou phononique ou par des porteurs libres. L’absorption dans l’UV est généralement due à des transitions électroniques, où l’énergie lumineuse excite les électrons vers des états élevés. La figure 5 montre que les constantes optiques hypothétiques ou réelles ne sont pas indépendantes, mais mathématiquement liées par les relations de Kramers-Kronig.

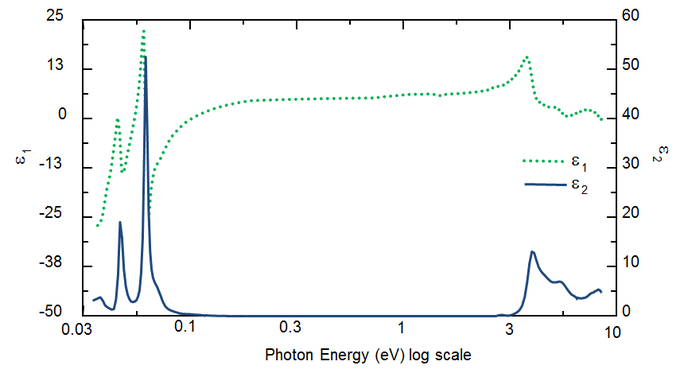
Figure 5 : Fonction diélectrique complexe pour un film de TiO2 avec des longueurs d’onde allant de l’IR (petits eV) à l’UV (hauts eV).

La lumière et l’interaction des matériaux

Chaque fois que la lumière interagit avec un matériau, cela conduit à des conditions limites à l’interface. Pendant ce temps, les équations de Maxwell doivent toujours rester satisfaites. La figure ci-dessous montre comment la lumière incidente se reflète et se réfracte à l’interface. L’angle entre le rayon incident et la normale de l’échantillon (θi) sera égal à l’angle réfléchi (θr). La lumière qui entre dans un matériau est réfractée à un angle θt donné par :

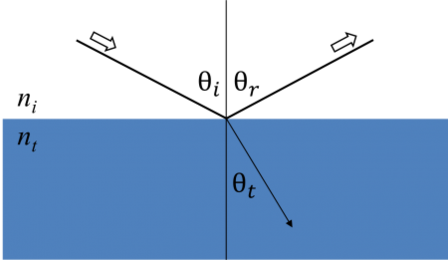
Figure 6 : La lumière se réfléchit et se réfracte selon la loi de Snell.

À chaque interface, une partie de la lumière est réfléchie tandis que le reste transmet à l’angle réfracté. Selon les conditions aux limites, différentes solutions s’appliquent pour les champs électriques parallèles et perpendiculaires à la surface de l’échantillon. La lumière peut ainsi être séparée en composantes orthogonales par rapport au plan d’incidence (polarisation p et s). Les deux composantes peuvent être calculées séparément. C’est ainsi que Fresnel a décrit la quantité de lumière réfléchie et transmise à une interface entre des matériaux :

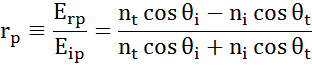
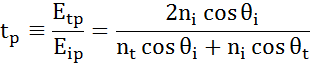
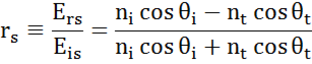
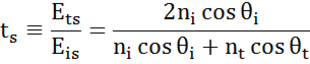
Des interfaces multiples avec des coefficients de réflexion et de transmission de Fresnel appropriés se produisent avec des couches minces et des structures multicouches. Pour définir correctement le faisceau réfléchi ou transmis, la phase relative de chaque composante lumineuse doit être suivie. L’épaisseur de phase du film est ainsi déterminée comme suit :

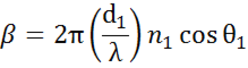
Lorsque plusieurs ondes lumineuses se superposent, il se produit une interférence qui dépend de la phase relative de chaque onde lumineuse individuelle. La figure ci-dessous montre la combinaison des ondes lumineuses dans le faisceau réfléchi et leurs calculs de Fresnel correspondants.

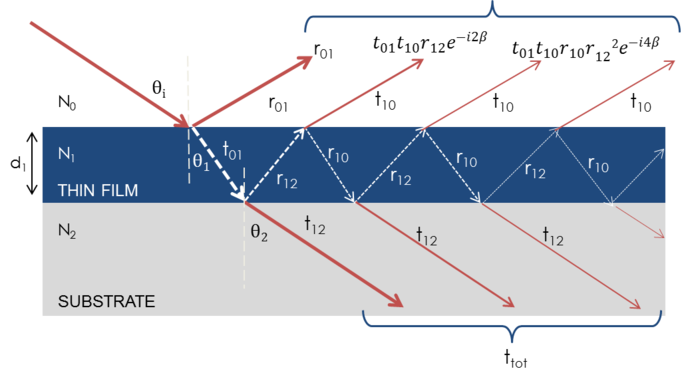
Figure 7 : La lumière se reflète et se réfracte à chaque interface individuelle, ce qui conduit à des faisceaux multiples dans un film mince. L’interférence des faisceaux dépend de la phase et de l’amplitude relatives des champs électriques. La réaction des faisceaux peut être calculée avec les coefficients de réflexion et de transmission de Fresnel.

Mesures

L’ellipsométrie mesure principalement la façon dont les composantes p et s réagissent l’une par rapport à l’autre pendant la réflexion ou la transmission. Un faisceau de référence fait donc toujours partie de l’expérience. Une polarisation connue est réfléchie ou transmise par l’échantillon et la polarisation de sortie est mesurée. Le changement de polarisation est la mesure d’ellipsométrie:

La figure 6 montre une mesure typique d’ellipsométrie d’un échantillon. La lumière incidente linéaire a les deux composantes p- et s-. La lumière réfléchie présente des changements d’amplitude et de phase pour la lumière polarisée p- et s-. Ces changements sont mesurés par ellipsométrie.

Pour recueillir des données d’ellipsométrie, il faut : une source de lumière, un générateur de polarisation, un échantillon, un analyseur de polarisation et un détecteur. Le générateur et l’analyseur de polarisation sont tous deux constitués de pièces optiques qui manipulent la polarisation : compensateurs, polariseurs et modulateurs de phase. Les configurations typiques d’un ellipsomètre comprennent un analyseur rotatif (RAE), un polariseur rotatif (RPE), un compensateur rotatif (RCE) et une modulation de phase (PME). La figure ci-dessous montre une configuration RAE.

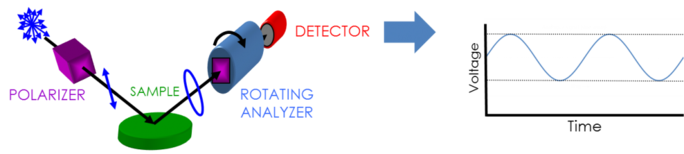
La lumière non polarisée est produite par une source lumineuse puis envoyée à travers un polariseur. Le polariseur est réglé pour ne laisser passer que la lumière ayant une certaine orientation du champ électrique. Comme l’axe du polariseur est aligné entre les plans p- et s-, les deux atteignent la surface de l’échantillon. La lumière, maintenant polarisée linéairement, est réfléchie par la surface de l’échantillon, devenant ainsi polarisée elliptiquement, puis envoyée à travers un polariseur en rotation continue (l' »analyseur »). La quantité de lumière qui peut passer dépend de l’orientation du polariseur par rapport à l’ellipse du champ électrique de l’échantillon. Pour définir la polarisation réfléchie, la lumière est convertie en un signal électronique dans le détecteur. La comparaison de ces données avec la polarisation d’entrée établie fournit des informations sur le changement causé par la réflexion de l’échantillon : la mesure ellipsométrique de Psi et Delta.

Analyse des données

L’ellipsométrie est utilisée pour définir l’épaisseur des films de matériaux ou les constantes optiques en mesurant les changements de polarisation de la lumière. Des « pseudo » constantes optiques issues de la mesure d’ellipsométrie peuvent être dérivées en inversant les données déterminées pour une seule réflexion. Ceci est utile pour les matériaux en vrac.

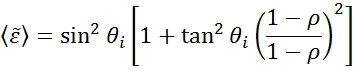
L’équation ci-dessus ne compte avec aucune couche de surface. Néanmoins, il y a normalement un oxyde de surface ou une rugosité dans les matériaux en vrac. Une inversion directe inclura ces données comme faisant partie des constantes optiques globales. Voir la fig. 10 pour une vue d’ensemble d’un processus d’analyse de données typique utilisé dans les mesures d’ellipsométrie. Comme il est impossible d’écrire une équation exacte, une analyse de régression est nécessaire. La réponse est souvent surdéterminée avec seulement quelques inconnues et des centaines de points de données expérimentales. Une analyse de régression permet d’inclure toutes les données mesurées pour déterminer la solution.

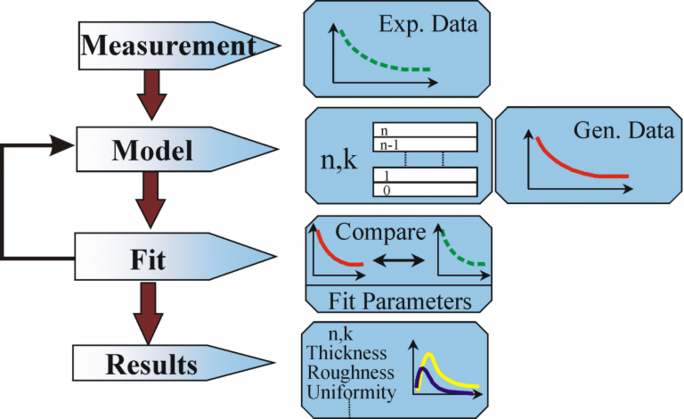
Figure 10 : Organigramme pour l’analyse des données d’ellipsométrie.

La procédure suivante est utilisée pour l’analyse des données : l’échantillon est mesuré et un modèle est fait de l’échantillon. A l’aide de ce modèle, les résultats supposés des équations de Fresnel, qui décrivent l’épaisseur et les constantes optiques de chaque matériau, sont calculés. Une évaluation du calcul préliminaire est faite, si ces valeurs sont inconnues. Les valeurs calculées sont comparées aux données expérimentales. Pour mieux faire correspondre les données expérimentales et les données de calcul, on peut faire varier les données inconnues des matériaux. Cependant, les points de données expérimentales doivent toujours être plus nombreux que les paramètres inconnus. Par exemple, au maximum deux propriétés du matériau peuvent être déterminées avec un ellipsomètre à une seule longueur d’onde, car il produit exactement deux points de données : Ψ, Δ (Psi et Delta). La régression est utilisée pour trouver la meilleure correspondance entre le modèle et l’expérience. La différence entre les courbes de données est quantifiée à l’aide d’un estimateur comme l’erreur quadratique moyenne (EQM). Les propriétés inconnues sont modifiées jusqu’à ce que l’EQM minimale soit atteinte. Cela signifie que l’EQM la plus faible équivaut à la meilleure réponse.

Voir la figure ci-dessous pour la courbe EQM en fonction de l’épaisseur du film pour un film transparent sur silicium. La valeur MSE la plus faible se produit à une épaisseur de 749 nm malgré un certain nombre de minima locaux. L’épaisseur correcte du film est donc également de 749 nm. L’algorithme de régression peut considérer qu’un minimum local est correct. Ainsi, pour déterminer le minimum global correct, il est judicieux de comparer les résultats à l’œil pour le MSE le plus bas.

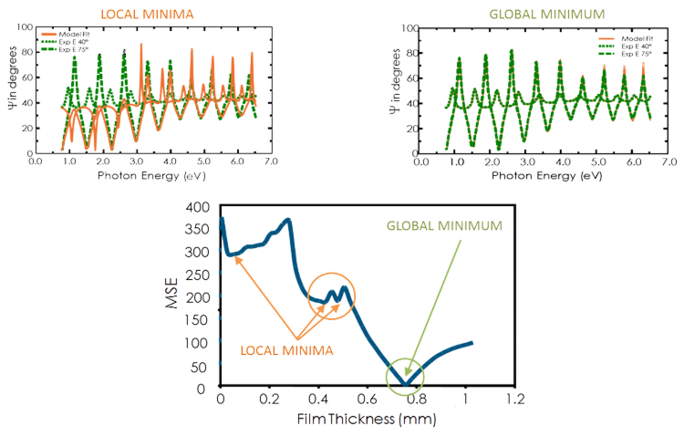
Figure 11, haut-droit : Données expérimentales et courbes correspondantes générées pour le modèle au minimum global. Figure 11, haut-gauche : Une courbe similaire au minimum local près d’une épaisseur de 0,45 µm peut facilement être identifiée comme un résultat incorrect. Figure 11, en bas : La courbe MSE en fonction de l’épaisseur montre le minimum global. Un algorithme de régression peut donner des minima locaux, mais pas le résultat final.

Détermination de l’épaisseur du film

L’épaisseur d’un film est généralement déterminée par l’interférence entre la lumière qui se réfléchit sur la surface et la lumière qui traverse le film. Le fait que cette interférence soit considérée comme constructive ou destructive dépend de la phase relative de la lumière qui se joint à la réflexion de la surface. L’interférence comprend à la fois des informations d’amplitude et de phase. L’information de phase de Δ est très sensible aux films jusqu’à l’épaisseur sous-monocouche. Voir la figure ci-dessous pour une comparaison de l’intensité réfléchie et de l’ellipsométrie pour la même série de couches minces de SiO2 sur Si. La réflectance pour chaque film est presque la même alors qu’il y a de grandes variations dans Δ.

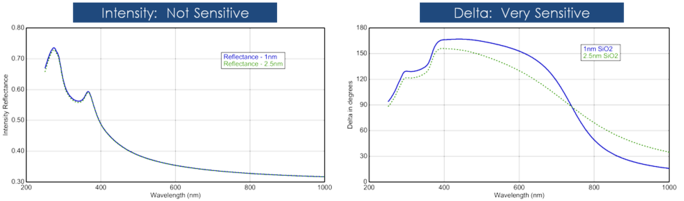
Figure 12, gauche : Intensité réfléchie et delta ellipsométrique (droite) pour deux oxydes minces sur silicium. La mesure de l’intensité ne montre pas que Delta est très sensible aux films d’échelle nanométrique.

L’ellipsométrie est couramment utilisée pour les films de sub-nanomètres à quelques microns d’épaisseur. Avec des films d’une épaisseur supérieure à plusieurs dizaines de microns, les oscillations d’interférence ne peuvent être résolues qu’avec une difficulté croissante, sauf si l’on utilise des longueurs d’onde infrarouges plus grandes. C’est pourquoi pour les films plus épais, d’autres techniques de mesure sont normalement utilisées.

Pour mesurer l’épaisseur, une partie de la lumière doit traverser le film complet et revenir à la surface. Avec les matériaux absorbant la lumière, les mesures d’épaisseur optiques ne peuvent être réalisées que sur des couches minces et semi-opaques, à moins qu’elles ne soient réalisées sur des régions spectrales moins absorbantes. Par exemple, un film organique qui absorbe la lumière UV et IR peut être transparent aux longueurs d’onde mi-visible. Les métaux absorbent fortement à toutes les longueurs d’onde, donc l’épaisseur maximale de la couche qui peut être déterminée fixe autour de 100 nm.

Constantes optiques

Les constantes optiques jouent un rôle important pour les mesures d’épaisseur. L’épaisseur d’un film influence la longueur du trajet de la lumière qui traverse le film, l’indice détermine la vitesse de l’onde lumineuse et l’angle de réfraction. Tous deux contribuent donc au délai entre la lumière qui traverse le film et la réflexion de la surface. Il est nécessaire d’établir n et k ainsi que l’épaisseur pour obtenir des résultats corrects d’une mesure optique.

Comme les constantes optiques d’un matériau varient pour différentes longueurs d’onde, toutes les longueurs d’onde qui sont analysées avec l’ellipsomètre doivent être déterminées individuellement. La réponse d’un matériau à chaque longueur d’onde peut être anticipée en utilisant un tableau de constantes optiques. Pour éviter l’ajustement laborieux de constantes optiques inconnues, longueur d’onde par longueur d’onde, il est préférable d’utiliser toutes les longueurs d’onde simultanément. Les paramètres ajustables d’une relation de dispersion, par exemple, permettent à la forme globale de la constante optique de correspondre aux résultats expérimentaux. Par rapport à l’ajustement des valeurs individuelles de n et k pour chaque longueur d’onde, le nombre de paramètres libres inconnus est considérablement réduit.

Les relations de Cauchy ou de Sellmeier sont fréquemment utilisées pour décrire l’indice des matériaux transparents où la relation de Cauchy est normalement donnée comme:

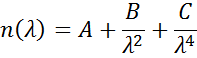
avec les trois termes ajustés pour correspondre à l’indice de réfraction du matériau. La relation de Cauchy n’est pas limitée par la cohérence de Kramers-Kronig (KK) et peut conduire à une dispersion non physique. La relation de Sellmeier, en revanche, impose la cohérence de Kramers-Kronig (KK), qui garantit que la dispersion optique conserve une forme réaliste. La relation de Sellmeier s’écrit généralement comme suit :

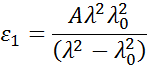
Les matériaux absorbants ont souvent une région de longueur d’onde transparente qui peut être modélisée avec la relation de Cauchy ou de Sellmeier. Alors que la région absorbante, cependant, doit tenir compte des constantes optiques réelles et imaginaires. Pour décrire l’absorption de divers matériaux, de nombreuses relations de dispersion utilisent la théorie de l’oscillateur, y compris Lorentz, Harmonic et Gauss. Elles partagent toutes des attributs similaires, les caractéristiques de l’absorption étant décrites par l’amplitude, l’élargissement et l’énergie centrale (liée à la fréquence de la lumière). La forme de la composante réelle est calculée en utilisant la cohérence de Kramers-Kronig après que le comportement imaginaire ait été décrit par l’oscillateur. Pour inclure une éventuelle absorption supplémentaire au-delà de la région spectrale mesurée, un décalage de la composante réelle est ajouté. L’oscillateur de Lorentz peut être écrit comme:

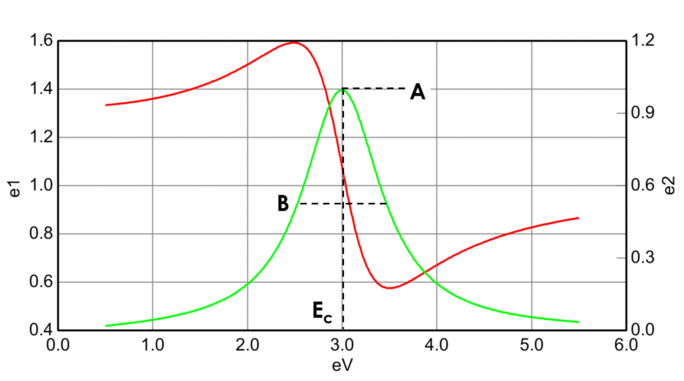
La figure 13 montre également l’amplitude (A), l’élargissement (B), l’énergie centrale (Ec) et le décalage (e1, off set) pour un oscillateur de Lorentz typique. L’énergie E est liée à la fréquence d’une onde, n:

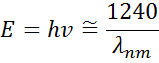
La constante de Planck h et la longueur d’onde λ sont données en nanomètres. D’autres modèles de dispersion, comme Tauc-Lorentz et Cody-Lorentz, incorporent des termes pour décrire l’énergie de la bande interdite.

Lecture complémentaire

L’ellipsométrie est une technique optique établie pour la mesure des films minces et des matériaux en vrac. Elle utilise les changements de polarisation causés par la réflexion/transmission à partir d’une structure matérielle pour déterminer les caractéristiques du matériau comme l’épaisseur et les constantes optiques.

Aspnes D.E. (1985). La détermination précise des propriétés optiques par ellipsométrie. In : Palik E.D. (ed.) Handbook of Optical Constants of Solids, pp. 89-112. Academic Press, Orlando.

Azzam R.M.A. et Bashara N.M. (1987). Ellipsométrie et lumière polarisée, Elsevier Science B.V., Amsterdam, Pays-Bas.

Boccara A.C., Pickering C., et Rivory J. (eds.), (1993). Spectroscopic Ellipsometry, Elsevier Publishing, Amsterdam.

Collins R.W., Aspnes D.E., et Irene E.A. (eds.), (1998). « Actes de la deuxième conférence internationale sur l’ellipsométrie spectroscopique ». In : Thin Solid Films, vols. 313-314.

Fujiwara H., Spectroscopic Ellipsometry, Principles and Applications, John Wiley & Sons, Ltd. 2007

Gottesfeld S., Kim Y.T., et Redondo A. (1995). « Applications récentes de l’ellipsométrie et de la spectroellipsométrie dans les systèmes électrochimiques », In : I. Rubinstein (ed.), Physical Electrochemistry : Principles, Methods, and Applications, Marcel Dekker, New York.

Herman, I.P. (1996). Diagnostics optiques pour le traitement des films minces, pp 425-479. Academic Press, San Diego, Californie.

Johs B. et al (1999).  » Aperçu de l’ellipsométrie spectroscopique à angle variable (VASE), partie II : applications avancées « . Optical Metrology, vol. CR72, pp 29-58. SPIE, Bellingham, Washington.

Johs B. et al (2001). « Développements récents de l’ellipsométrie spectroscopique pour les applications in situ ». In : Duparré A, Singh B (ed.) Optical Metrology Roadmap for the Semiconductor, Optical, and Data Storage Industries II, vol. 4449, pp 41-57. SPIE, Bellingham, Washington.

Roseler A. (1990). Ellipsométrie spectroscopique infrarouge, Akademie-Verlag, Berlin.

Rossow U. et Richter W. (1996). « Ellipsométrie spectroscopique » in : Bauer G et Richter W (eds.) Optical Characterization of Epitaxial Semiconductor Layers, pp. 68-128, Springer-Verlag, Berlin.

Tompkins H.G. (1993). A User’s Guide to Ellipsometry, Academic Press, San Diego, Californie.

Tompkins H.G. et McGahan W.A. (1999). Spectroscopic Ellipsometry and Reflectometry, John Wiley & Sons, Inc, USA.

Tompkins, H.G. et Irene E.A. (eds.), 2005, Handbook of Ellipsometry, William Andrew Publishing, New York.

Tompkins, H. G. et Hilfiker, J. H., Ellipsométrie spectroscopique, application pratique à la caractérisation des couches minces, 2016, Momentum Press Engineering

Woollam J.A. et Snyder P.G. (1992). « Ellipsométrie spectroscopique à angle variable » in : Brundle CR, Evans CA, et Wilson S (eds) Encyclopedia of Materials Characterization : Surfaces, Interfaces, Thin Films, pp. 401-411, Butterworth-Heinemann, Boston.

Woollam J.A. et al (1999).  » Aperçu de l’ellipsométrie spectroscopique à angle variable (VASE), partie I : théorie de base et applications typiques « . Optical Metrology, vol. CR72, pp 3-28. SPIE, Bellingham, Washington.

Woollam J.A. (2000). « Ellipsométrie, spectroscopique à angle variable » in : Webster J.G. (ed.) Wiley Encyclopedia of Electrical and Electronics Engineering, pp. 109-116. John Wiley & Sons, New York.