Combien connaissez-vous les infinis ? Vous avez probablement entendu parler d’un nombre qui est le plus grand nombre possible, ou impossiblement grand.

Pour expliquer les infinis, je dois d’abord définir une certaine terminologie.

Les entiers sont des nombres utilisés pour compter. L’ensemble des nombres entiers est défini comme l’ensemble des nombres sans composante fractionnaire. Quelques exemples sont : -12, 0, 1, 3, 42, 17.

L’infini est le concept d’un objet hors de portée des nombres naturels. Il a été conceptualisé pour la première fois par un mathématicien russe nommé Georg Cantor, qui a non seulement introduit l’infini, mais a également révélé qu’il y avait de multiples infinis qui existaient.

Cantor a fourni une preuve controversée des infinis, qui disait que certains infinis étaient plus grands que d’autres. Au début, cela peut sembler impossible – comment un objet peut-il être plus grand qu’un autre objet infini ?

Cantor a basé sa preuve sur une branche des mathématiques apparemment inutile : la théorie des ensembles. Un ensemble est une collection d’objets – par exemple, nous pouvons avoir un ensemble contenant 1, 2 et 3. Ces objets dans l’ensemble sont appelés des éléments.

En notation mathématique, cela ressemblerait à :

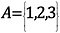
Le nombre d’éléments dans cet ensemble, ou la Cardinalité de l’ensemble, est 3.

Ceci est noté comme :

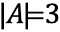
Si nous avons maintenant un autre ensemble, B, contenant des objets, tel que

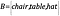
Comment savons-nous que les ensembles ont la même taille ?

Une façon de le voir est de compter le nombre d’éléments dans le deuxième ensemble. Nous pouvons clairement voir que cet ensemble a également 3 éléments, et donc nous savons qu’ils ont la même taille.

Une autre façon de le faire est de comparer notre deuxième ensemble, B, à notre premier ensemble, A par mappage.

Nous pouvons mapper le premier élément de l’ensemble A , 1, au premier élément de l’ensemble B, chaise.

Nous pouvons mettre en correspondance le deuxième élément de l’ensemble A, 2, avec le deuxième élément de l’ensemble B, table.

Nous pouvons mettre en correspondance le troisième élément de l’ensemble A, 3, avec le troisième élément de l’ensemble B, chapeau.

Puisque chaque élément de A est mis en correspondance avec exactement 1 élément de B, les ensembles ont une taille égale.

Regardons maintenant les ensembles infinis. L’ensemble des entiers, qui a été mentionné au début, est un ensemble infini – il y a un nombre infini d’entiers. L’ensemble des nombres entiers est dénoté par le symbole

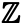
L’ensemble des nombres pairs, que nous pouvons désigner par

est défini comme

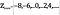
Intuitivement, il peut sembler que

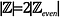
comme il y a 2 entiers pour chaque entier pair : 1 entier impair et 1 entier pair. Vérifions cela.

Essayons de comparer les ensembles en faisant correspondre les éléments de 1 ensemble à l’autre.

Nous pouvons faire correspondre 1 à 2, 2 à 4, 3 à 6, et ainsi de suite.

Si cela continue à travers les ensembles, nous pouvons voir que chaque élément de l’ensemble des nombres entiers se mappe sur exactement 1 élément de l’ensemble des nombres entiers pairs.

Ainsi, bien que cela puisse sembler contre-intuitif, la taille des ensembles est égale.