Radiation électromagnétique
L’énergie qui est transmise, ou rayonnée, à travers l’espace sous la forme d’oscillations périodiques de champs électriques et magnétiques est connue sous le nom de radiation électromagnétique. (Figure \(\PageIndex{2}\)). La figure \(\PageIndex{4}\) illustre certaines formes de rayonnement électromagnétique. Dans le vide, toutes les formes de rayonnement électromagnétique, qu’il s’agisse de micro-ondes, de lumière visible ou de rayons gamma, se déplacent à la vitesse de la lumière (c), qui est la vitesse à laquelle toutes les formes de rayonnement électromagnétique se déplacent dans le vide, une constante physique fondamentale dont la valeur est de 2,99792458 × 108 m/s (soit environ 3,00 ×108 m/s ou 1,86 × 105 mi/s). C’est environ un million de fois plus rapide que la vitesse du son.
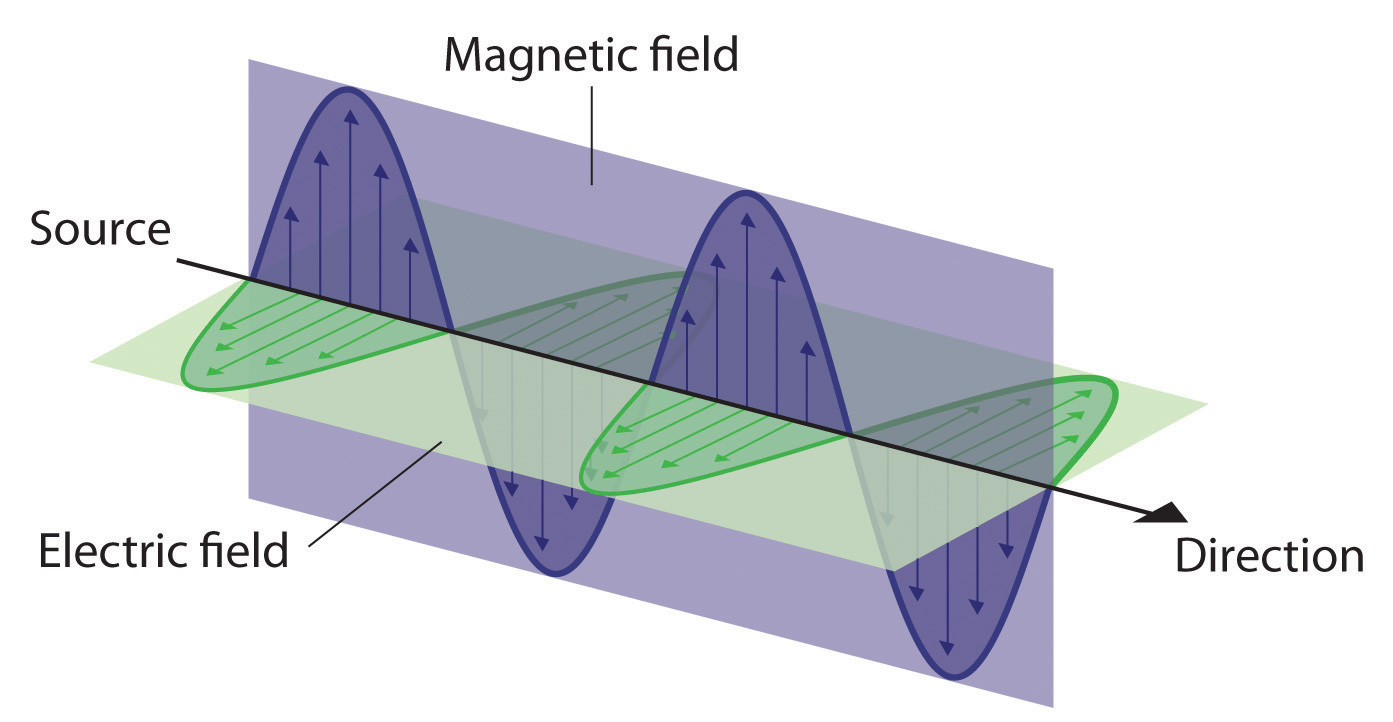
Parce que les différents types de rayonnement électromagnétique ont tous la même vitesse (c), ils ne diffèrent que par la longueur d’onde et la fréquence. Comme le montrent la figure \(\PageIndex{3}\) et le tableau \(\PageIndex{1}\), les longueurs d’onde des rayonnements électromagnétiques connus vont de 101 m pour les ondes radio à 10-12 m pour les rayons gamma, qui sont émis par les réactions nucléaires. En observant l’équation ci-dessous, nous pouvons voir comment la fréquence d’un rayonnement électromagnétique est inversement proportionnelle à sa longueur d’onde :
\
Par exemple, la fréquence des ondes radio est d’environ 108 Hz, alors que la fréquence des rayons gamma est d’environ 1020 Hz. La lumière visible, qui est un rayonnement électromagnétique pouvant être détecté par l’œil humain, a une longueur d’onde comprise entre environ 7 × 10-7 m (700 nm, ou 4,3 × 1014 Hz) et 4 × 10-7 m (400 nm, ou 7,5 × 1014 Hz). Notez que lorsque la fréquence augmente, la longueur d’onde diminue ; c étant une constante reste la même. De même lorsque la fréquence diminue, la longueur d’onde augmente.
Veuillez mémoriser l’équation 5.2.1 et la vitesse de la lumière (avec les unités). En outre, il est important de savoir quel côté du spectre électromagnétique est mortel.
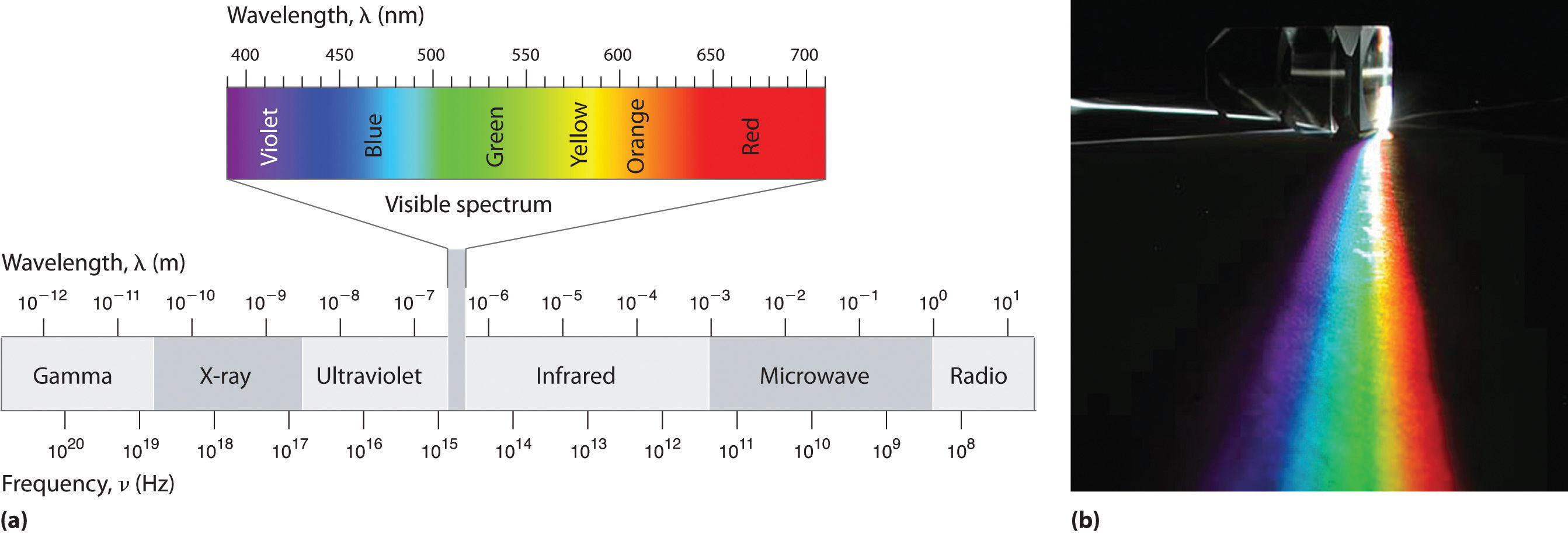
| Unité | Symbole | Longueur d’onde (m) | Type de rayonnement |
|---|---|---|---|
| picomètre | pm | 10-12 | rayon gamma |
| nanomètre | nm | 10-9 | x-.ray |
| micromètre | μm | 10-6 | infrarouge |
| millimètre | mm | 10-3 | infrarouge |
| centimètre | cm | 10-2 | micro-ondes |
| mètre | m | 100 | radio |
La lumière se comporte également comme un paquet d’énergie. Il s’avère que pour la lumière, l’énergie du « paquet » d’énergie est proportionnelle à sa fréquence.
\
Alors que la lumière visible est essentiellement inoffensive pour notre peau, la lumière ultraviolette, avec des longueurs d’onde de ≤ 400 nm, a suffisamment d’énergie pour causer de graves dommages à notre peau sous la forme de coups de soleil. Parce que la couche d’ozone absorbe la lumière solaire avec des longueurs d’onde inférieures à 350 nm, elle nous protège des effets dommageables du rayonnement ultraviolet hautement énergétique.
Dans ce cours, nous ne ferons pas de calculs d’énergie. Vous devriez connaître la relation entre la fréquence et l’énergie. De plus, vous montrez réaliser que le rayonnement de courte longueur d’onde est associé à une énergie élevée.
L’énergie du rayonnement électromagnétique augmente avec l’augmentation de la fréquence et la diminution de la longueur d’onde.
Exemple \(\PageIndex{1}\)
Quelle est la fréquence de la lumière si sa longueur d’onde est de 5,55 × 10-7 m?
Solution
Nous utilisons l’équation qui relie la longueur d’onde et la fréquence de la lumière à sa vitesse. Nous avons
\N
Nous divisons les deux côtés de l’équation par 5,55 × 10-7 m et obtenons
\N
Notez comment les unités m s’annulent, laissant s au dénominateur. Une unité dans un dénominateur est indiquée par une puissance -1-s-1-et se lit comme « par seconde. »
Exercice \(\PageIndex{1}\)
Quelle est la longueur d’onde (en mm) de la lumière si sa fréquence est de 1.55 × 1010 s-1?
Réponse
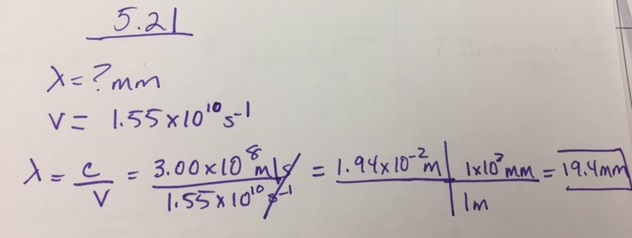
Exemple \(\PageIndex{2}\)
Calculez la fréquence d’une radiation si sa longueur d’onde est de 988 nm. Où cette radiation apparaît-elle dans le spectre électromagnétique ?
Réponse
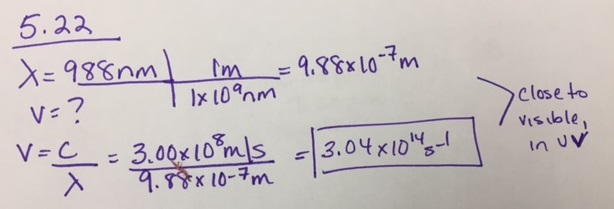
.