Die Varianz ist eine Zahl, die angibt, wie weit eine Menge von Zahlen auseinander liegt.Die Varianz ist identisch mit der quadrierten Standardabweichung und drückt somit „das Gleiche“ aus (aber stärker).

Varianz – Beispiel

Eine Studie lässt 100 Personen eine einfache Geschwindigkeitsaufgabe während 80 Versuchen durchführen. Für jeden Teilnehmer werden also 80 Reaktionszeiten (in Sekunden) aufgezeichnet. Ein Teil dieser Daten ist im Folgenden dargestellt.

In Studien wie dieser ist typischerweise zu beobachten, dass die Personen schneller werden, wenn sie die Geschwindigkeitsaufgabe häufiger durchführen. Das heißt, die durchschnittliche Reaktionszeit nimmt über die Versuche hinweg ab.
Auch variieren die Reaktionszeiten typischerweise weniger zwischen verschiedenen Personen, je öfter sie die Aufgabe durchführen. Technisch gesehen sagen wir, dass die Varianz über die Versuche abnimmt. Die nachstehende Tabelle veranschaulicht dies für die Versuche 1, 4, 7 und 10.

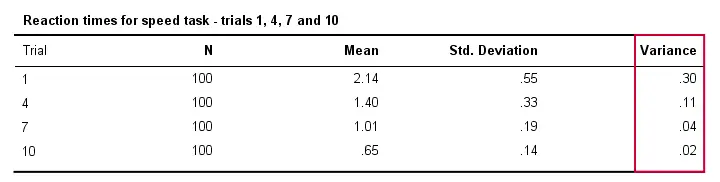
Varianz und Histogramm

Eine gute Möglichkeit zur Visualisierung der Daten aus unserer vorherigen Tabelle ist ein Histogramm für jeden Versuch. So veranschaulicht die folgende Abbildung, dass die Teilnehmer im Laufe der Versuche schneller wurden; von Versuch 1 bis Versuch 10 bewegen sich die Histogrammbalken nach links, in Richtung 0 Sekunden.

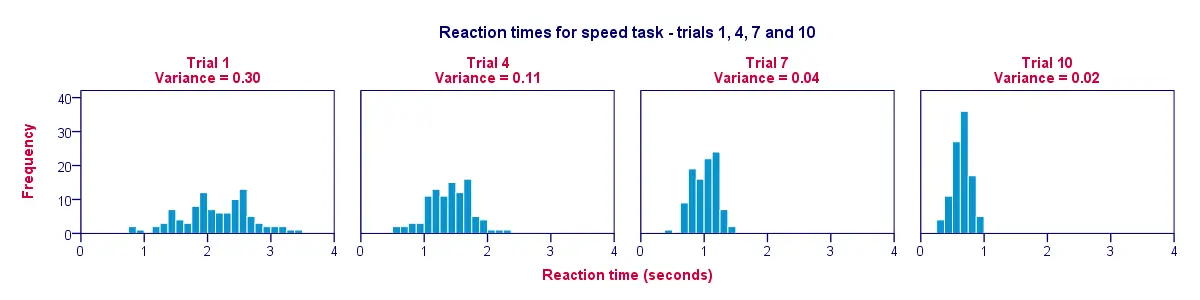
Eine zweite Erkenntnis ist, dass die Histogramme schmaler (und damit höher) werden, wenn wir uns von Versuch 1 bis Versuch 10 bewegen; dies veranschaulicht, dass die Reaktionszeiten zwischen unseren Teilnehmern im Laufe des Experiments immer weniger variieren. Die Varianz nimmt im Laufe der Versuche ab.

Varianz – Populationsformel

Eine grundlegende Formel zur Berechnung der Varianz lautet

$$S^2 = \frac{\sum(X – \overline{X})^2}{n}$$

Wir empfehlen Ihnen, zu versuchen zu verstehen, was diese Formel bewirkt, denn sie hilft sehr beim Verständnis der ANOVA (= Varianzanalyse). Wir werden sie daher an einer Handvoll Daten demonstrieren.

Varianz – GoogleSheets

Der Einfachheit halber beschränken wir unsere Daten auf den ersten Versuch für die ersten 5 Teilnehmer. Diese 5 Reaktionszeiten – und eine manuelle Berechnung ihrer Varianz – befinden sich in diesem GoogleSheet.

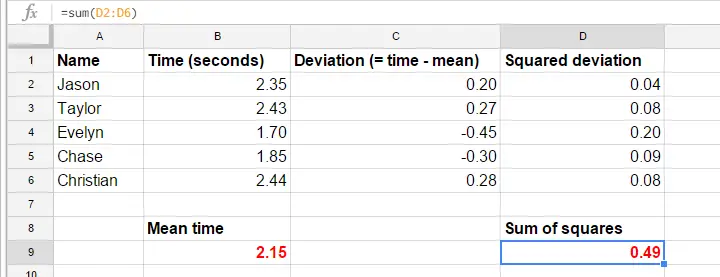
Varianz – Berechnungsschritte

Die Formeln im GoogleSheet zeigen genau, wie man eine Varianz berechnet. Die grundlegenden Schritte sind

1. Berechnen Sie die mittlere Reaktionszeit (2,15);
2. Berechnen Sie die Abweichungswerte (Reaktionszeit minus mittlere Reaktionszeit);
3. Berechnen Sie die quadrierten Abweichungswerte;
4. Addieren Sie die quadrierten Abweichungswerte. Das Ergebnis (0,49) ist die Summe der Quadrate, der Hauptbaustein der ANOVA;
5. dividieren Sie die Summe der Quadrate durch die Anzahl der Beobachtungen (5 Reaktionszeiten).

Alternativ können Sie eine Varianz berechnen, indem Sie =VARP(B2:B6) in eine Zelle eingeben (B2:B6 sind die Zellen, die unsere 5 Reaktionszeiten enthalten). VARP ist die Abkürzung für „Varianzpopulation“. OpenOffice und MS Excel enthalten ähnliche Formeln.

Varianz – Stichprobenformel

Wenn es sich bei unseren Daten um eine einfache Zufallsstichprobe aus einer viel größeren Grundgesamtheit handelt, wird die oben genannte Formel die Varianz der Grundgesamtheit systematisch unterschätzen, ähnlich wie bei der Standardabweichung. In diesem Fall verwenden wir eine etwas andere Formel:

$$S^2 = \frac{\sum(X_i – \overline{X})^2}{n – 1}$$

Welche Formel wir verwenden, hängt also von unseren Daten ab: enthalten sie die gesamte Grundgesamtheit, die wir untersuchen möchten, oder sind sie nur eine Stichprobe aus dieser Grundgesamtheit?
Da unsere 100 Teilnehmer eindeutig eine Stichprobe sind, verwenden wir die Stichprobenformel. In GoogleSheets gibt die Eingabe von =VAR(B2:B6) in eine Zelle die Varianz der Stichprobe zurück.

Varianz in SPSS

Soweit wir wissen, fehlt die Formel für die Varianz der Grundgesamtheit in SPSS völlig, was wir für einen schwerwiegenden Fehler halten. SPSS verwendet stattdessen immer die Stichprobenformel, und zwar sowohl für die Varianz zwischen den Probanden (die in diesem Tutorial behandelt wird) als auch für die Varianz innerhalb der Probanden. Die entsprechende Ausgabe ist unten abgebildet.

Bezüglich dieser Ausgabetabelle ist auch zu beachten, dass die Varianz tatsächlich die quadrierte Standardabweichung ist (abgesehen von der Rundung).

Bezüglich der Varianz, das war’s. Wir hoffen, dass Ihnen dieses Tutorial geholfen hat, zu verstehen, was eine Varianz ist.