Unerwünschte Faltung ist ein inhärentes Problem bei der Übertragung analoger Informationen. Zum Beispiel kann alles Folgende als Faltung modelliert werden: Bildunschärfe bei einer verwackelten Kamera, Echos bei Ferngesprächen, die unbegrenzte Bandbreite analoger Sensoren und Elektronik usw. Entfaltung ist der Prozess der Filterung eines Signals, um eine unerwünschte Faltung zu kompensieren. Ziel der Entfaltung ist es, das Signal so wiederherzustellen, wie es vor der Faltung vorlag. Dazu müssen in der Regel die Merkmale der Faltung (d. h. die Impuls- oder Frequenzantwort) bekannt sein. Dies ist zu unterscheiden von der blinden Dekonvolution, bei der die Eigenschaften der parasitären Faltung nicht bekannt sind. Die blinde Entfaltung ist ein viel schwierigeres Problem, für das es keine allgemeine Lösung gibt, und der Ansatz muss auf die jeweilige Anwendung zugeschnitten sein.
Die Entfaltung ist im Zeitbereich fast unmöglich zu verstehen, im Frequenzbereich jedoch recht einfach. Jede Sinuskurve, aus der das ursprüngliche Signal besteht, kann beim Durchlaufen der unerwünschten Faltung in Amplitude und/oder Phase verändert werden. Um das ursprüngliche Signal zu extrahieren, muss der Entfaltungsfilter diese Amplituden- und Phasenänderungen rückgängig machen.
Wenn zum Beispiel die Faltung die Amplitude einer Sinuskurve um 0,5 mit einer Phasenverschiebung von 30 Grad verändert, muss der Entfaltungsfilter die Sinuskurve um 2,0 mit einer Phasenverschiebung von -30 Grad verstärken.
Das Beispiel, das wir zur Veranschaulichung der Entfaltung verwenden, ist ein Gammastrahlendetektor. Wie in Abb. 17-3 dargestellt, besteht dieses Gerät aus zwei Teilen, einem Szintillator und einem Lichtdetektor. Ein Szintillator ist eine besondere Art von transparentem Material wie Natriumiodid oder Wismutgermanat. Diese Verbindungen wandeln die Energie jeder Gammastrahlung in einen kurzen Ausbruch von sichtbarem Licht um. Dieses Licht
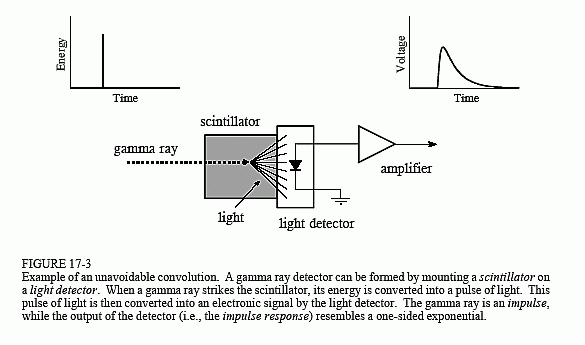
wird dann von einem Lichtdetektor, z. B. einer Photodiode oder Photomultiplier-Röhre, in ein elektronisches Signal umgewandelt. Jeder vom Detektor erzeugte Impuls entspricht einer einseitigen Exponentialkurve mit einer gewissen Abrundung an den Ecken. Diese Form wird durch die Eigenschaften des verwendeten Szintillators bestimmt. Wenn ein Ammastrahl seine Energie in den Szintillator abgibt, werden Atome in der Nähe auf ein höheres Energieniveau angeregt. Diese Atome deexzitieren nach dem Zufallsprinzip und erzeugen dabei jeweils ein einzelnes Photon des sichtbaren Lichts. Das Ergebnis ist ein Lichtimpuls, dessen Amplitude im Laufe einiger hundert Nanosekunden (bei Natriumiodid) abklingt. Da die Ankunft jedes Gamma-Strahls ein Impuls ist, ist der Ausgangsimpuls des Detektors (d.h. das einseitige Exponential) die Impulsantwort des Systems.
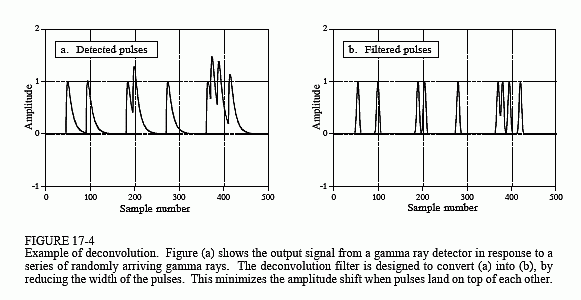
Abbildung 17-4a zeigt die Impulse, die der Detektor als Reaktion auf zufällig eintreffende Gammastrahlen erzeugt. Die Information, die wir aus diesem Ausgangssignal extrahieren möchten, ist die Amplitude jedes Impulses, die proportional zur Energie des Gammastrahls ist, der ihn erzeugt hat. Dies ist eine nützliche Information, denn die Energie kann interessante Informationen darüber liefern, wo die Gammastrahlung gewesen ist. Sie kann zum Beispiel medizinische Informationen über einen Patienten liefern, das Alter einer weit entfernten Galaxie bestimmen, eine Bombe im Gepäck einer Fluggesellschaft aufspüren, usw.
Alles wäre in Ordnung, wenn nur gelegentlich ein Gammastrahl entdeckt würde, aber das ist normalerweise nicht der Fall. Wie in (a) gezeigt, können sich zwei oder mehr Pulse überlappen, wodurch sich die gemessene Amplitude verschiebt. Eine Lösung für dieses Problem ist die Entfaltung des Ausgangssignals des Detektors, wodurch die Pulse schmaler werden, so dass es zu weniger Überlagerungen kommt. Im Idealfall sollte jeder Impuls dem Originalimpuls ähneln. Wie Sie vielleicht vermuten, ist dies nicht möglich, und wir müssen uns mit einem Impuls zufrieden geben, der zwar endlich lang, aber deutlich kürzer als der erkannte Impuls ist. Dieses Ziel ist in Abb. 17-4b dargestellt.
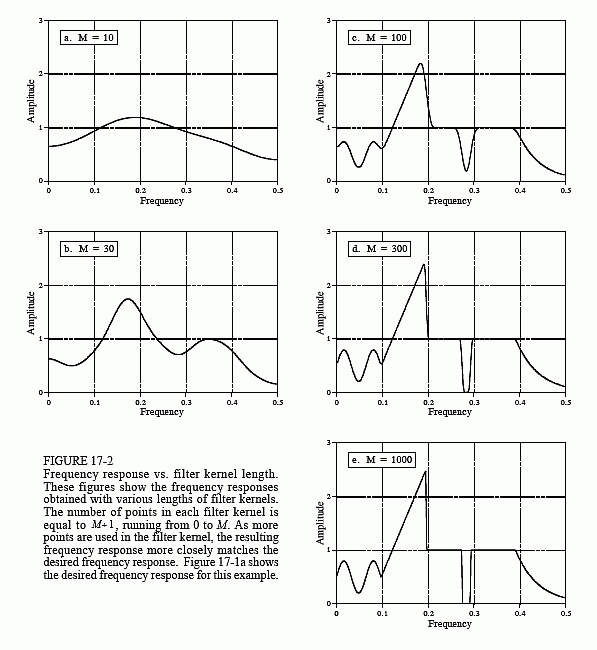
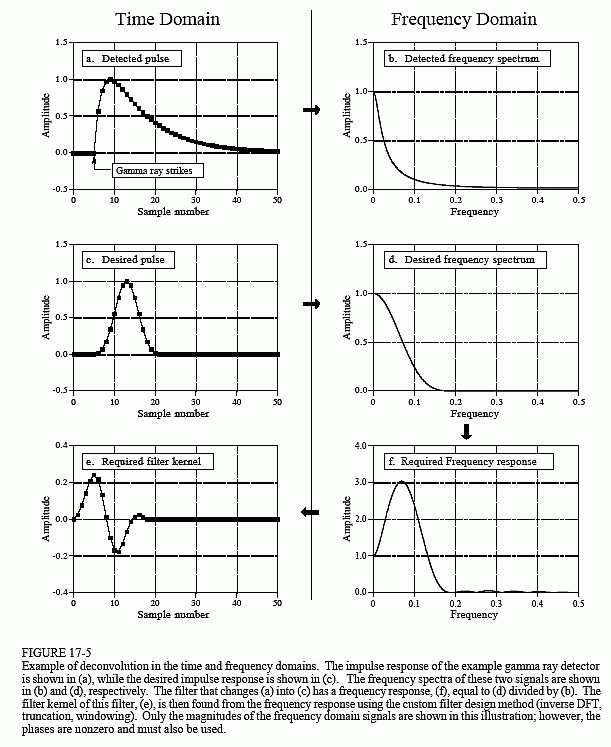
Auch wenn die Informationen des Detektorsignals im Zeitbereich kodiert sind, muss ein Großteil unserer Analyse im Frequenzbereich durchgeführt werden, wo das Problem leichter zu verstehen ist. Abbildung 17-5a ist das vom Detektor erzeugte Signal (das wir kennen). Abbildung (c) ist das Signal, das wir uns wünschen (ebenfalls etwas, das wir kennen). Dieser gewünschte Impuls wurde willkürlich so gewählt, dass er die gleiche Form wie ein Blackman-Fenster hat, mit einer Länge von etwa einem Drittel der Länge des ursprünglichen Impulses. Unser Ziel ist es, einen Filterkern (e) zu finden, der, wenn er mit dem Signal in (a) konvolviert wird, das Signal in (c) erzeugt. In Gleichungsform: wenn a * e = c, und gegeben a und c, finde.
Wenn diese Signale durch Addition oder Multiplikation anstelle der Faltung kombiniert würden, wäre die Lösung einfach: Subtraktion wird verwendet, um „de-addieren“ und Division wird verwendet, um „de-multiplizieren“. Bei der Faltung ist das anders; es gibt keine einfache inverse Operation, die als „Entfaltung“ bezeichnet werden kann. Die Faltung ist zu chaotisch, um sie durch direkte Manipulation der Zeitbereichssignale rückgängig zu machen.
Glücklicherweise ist dieses Problem im Frequenzbereich einfacher. Denken Sie daran, dass die Faltung in einem Bereich der Multiplikation im anderen Bereich entspricht. Nochmals zu den Signalen in Abb. 17-5: Wenn b × f = d ist und b und d gegeben sind, finden Sie f. Dies ist ein leicht zu lösendes Problem: Der Frequenzgang des Filters (f) ist das Frequenzspektrum des gewünschten Impulses (d) geteilt durch das Frequenzspektrum des erfassten Impulses (b). Da der erfasste Impuls asymmetrisch ist, hat er eine Phase ungleich Null. Das bedeutet, dass eine komplexe Division verwendet werden muss (d.h. eine Phase mit einem Betrag & geteilt durch eine andere Phase mit einem Betrag &). Falls Sie es vergessen haben, in Kapitel 9 wird beschrieben, wie man eine komplexe Division eines Spektrums durch ein anderes durchführt. Der erforderliche Filterkern (e) wird dann aus dem Frequenzgang durch die benutzerdefinierte Filtermethode (IDFT, Verschiebung, Abschneiden, &Multiplizieren mit einem Fenster) ermittelt.
Es gibt Grenzen für die Verbesserung, die die Entfaltung bieten kann. Mit anderen Worten: Wenn man zu gierig wird, geht die Sache schief. Gierig zu werden bedeutet in diesem Beispiel, dass man versucht, den gewünschten Impuls übermäßig schmal zu machen. Schauen wir uns an, was dann passiert. Wenn der gewünschte Impuls schmaler wird, muss sein Frequenzspektrum mehr hochfrequente Komponenten enthalten. Da diese Hochfrequenzkomponenten im erkannten Impuls eine sehr geringe Amplitude haben, muss der Filter bei diesen Frequenzen eine sehr hohe Verstärkung aufweisen. (f) zeigt zum Beispiel, dass einige Frequenzen mit dem Faktor drei multipliziert werden müssen, um den gewünschten Impuls in (c) zu erhalten. Wenn der gewünschte Impuls schmaler wird, ist die Verstärkung des Entfaltungsfilters bei hohen Frequenzen noch größer.
Das Problem ist, dass kleine Fehler in dieser Situation sehr unnachgiebig sind. Wenn zum Beispiel eine Frequenz um 30 verstärkt wird, obwohl nur 28 erforderlich ist, wird das entfaltete Signal wahrscheinlich ein Chaos sein. Wenn die Entfaltung auf ein höheres Leistungsniveau gebracht wird, müssen die Eigenschaften der unerwünschten Faltung mit größerer Genauigkeit und Präzision verstanden werden. In realen Anwendungen gibt es immer Unbekannte, die durch Schurken wie elektronisches Rauschen, Temperaturdrift, Schwankungen zwischen Geräten usw. verursacht werden. Diese Unbekannten schränken die Leistungsfähigkeit der Entfaltung ein.
Selbst wenn die unerwünschte Faltung perfekt verstanden wird, gibt es immer noch eine Tatsache, die die Leistungsfähigkeit der Entfaltung einschränkt: Rauschen. So haben die meisten unerwünschten Faltungen die Form eines Tiefpassfilters, der die Amplitude der Hochfrequenzkomponenten des Signals reduziert. Die Entfaltung korrigiert dies durch Verstärkung dieser Frequenzen. Wenn die Amplitude dieser Komponenten jedoch unter das Eigenrauschen des Systems fällt, geht die in diesen Frequenzen enthaltene Information verloren. Keine noch so gute Signalverarbeitung kann sie wiederherstellen. Sie ist für immer verloren. Adios! Auf Wiedersehen! Sayonara! Der Versuch, diese Daten zurückzugewinnen, wird nur das Rauschen verstärken. Im Extremfall kann die Amplitude einiger Frequenzen vollständig auf Null reduziert werden. Dadurch werden nicht nur die Informationen ausgelöscht, sondern es wird auch versucht, dem Entfaltungsfilter bei diesen Frequenzen eine unendliche Verstärkung zu geben. Die Lösung: Entwerfen Sie einen weniger aggressiven Entfaltungsfilter und/oder setzen Sie Grenzen für die zulässige Verstärkung bei einer der Frequenzen.
Wie weit darf man gehen? Wie gierig ist zu gierig? Das hängt ganz von dem Problem ab, das Sie angehen wollen. Wenn sich das Signal gut verhält und wenig Rauschen hat, kann man wahrscheinlich eine signifikante Verbesserung erzielen (man denke an einen Faktor 5-10). Wenn sich das Signal im Laufe der Zeit ändert, nicht besonders gut verstanden wird oder verrauscht ist, werden Sie nicht annähernd so gut abschneiden (denken Sie an einen Faktor von 1-2). Eine erfolgreiche Dekonvolution erfordert eine Menge Tests. Wenn es auf einer bestimmten Ebene funktioniert, versuchen Sie, weiter zu gehen; Sie werden es merken, wenn es zusammenbricht. Keine noch so große theoretische Arbeit wird es Ihnen ermöglichen, diesen iterativen Prozess zu umgehen.
Die Entfaltung kann auch auf im Frequenzbereich kodierte Signale angewendet werden. Ein klassisches Beispiel ist die Restaurierung von alten Aufnahmen des berühmten Opernsängers Enrico Caruso (1873-1921). Diese Aufnahmen wurden mit einer für heutige Verhältnisse sehr primitiven Ausrüstung gemacht. Das größte Problem sind die Resonanzen des langen röhrenförmigen Aufnahmehorns, das zur Aufnahme des Tons verwendet wurde. Immer wenn der Sänger auf eine dieser Resonanzfrequenzen trifft, steigt die Lautstärke der Aufnahme schlagartig an. Die digitale Entfaltung hat die subjektive Qualität dieser Aufnahmen verbessert, indem
die lauten Stellen in der Musik reduziert wurden. Wir beschreiben hier nur die allgemeine Methode; eine detaillierte Beschreibung finden Sie in der Originalarbeit: T. Stockham, T. Cannon, andR. Ingebretsen, „Blind Deconvolution Through Digital Signal Processing“,Proc. IEEE, vol. 63, Apr. 1975, pp. 678-692.
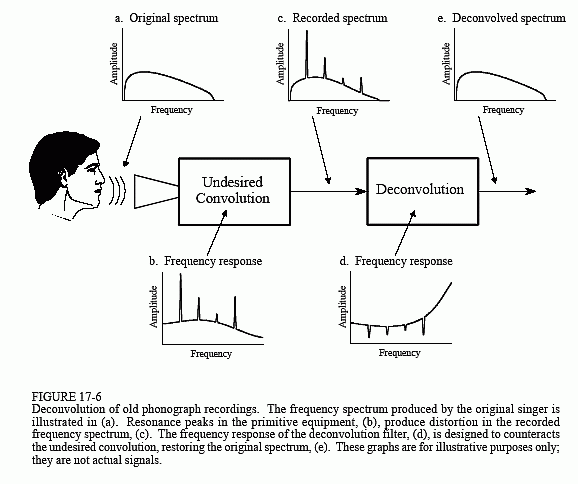
Abbildung 17-6 zeigt den allgemeinen Ansatz. Das Frequenzspektrum des ursprünglichen Audiosignals ist in (a) dargestellt. Abbildung (b) zeigt die Frequenzantwort des Aufnahmegeräts, eine relativ glatte Kurve mit Ausnahme einiger scharfer Resonanzspitzen. Das Spektrum des aufgezeichneten Signals, dargestellt in(c), entspricht dem wahren Spektrum (a), multipliziert mit dem ungleichmäßigen Frequenzgang (b). Das Ziel der Entfaltung ist es, der unerwünschten Entfaltung entgegenzuwirken. Mit anderen Worten: Der Frequenzgang des Entfaltungsfilters, (d), muss der Kehrwert von (b) sein. Das heißt, jede Spitze in (b) wird durch eine entsprechende Senke in (d) aufgehoben. Wäre dieser Filter perfekt konstruiert, hätte das resultierende Signal ein Spektrum (e), das mit dem des Originals identisch wäre.
Der Haken an der Sache ist, dass das ursprüngliche Aufnahmegerät längst ausrangiert wurde und sein Frequenzgang (b) ein Rätsel ist. Mit anderen Worten, es handelt sich um ein Blinddeconvolution-Problem; wenn wir nur (c) haben, wie können wir dann (d) bestimmen?
Blinden Entfaltungsproblemen begegnet man gewöhnlich, indem man eine Schätzung oder Annahme über die unbekannten Parameter vornimmt. In diesem Beispiel wird angenommen, dass das durchschnittliche Spektrum der Originalmusik mit dem durchschnittlichen Spektrum der gleichen Musik übereinstimmt, die von einem heutigen Sänger mit modernen Geräten vorgetragen wird. Das durchschnittliche Spektrum wird mit Hilfe der in Kapitel 9 beschriebenen Techniken ermittelt: Das Signal wird in eine große Anzahl von Segmenten zerlegt, die DFT jedes Segments berechnet, in die Polarform umgewandelt und dann der Mittelwert der Beträge gebildet. Im einfachsten Fall wird der unbekannte Frequenzgang als das durchschnittliche Spektrum der alten Aufnahme geteilt durch das durchschnittliche Spektrum der modernen Aufnahme ermittelt. (Die von Stockham et al. verwendete Methode basiert auf einer ausgefeilteren Technik, der so genannten homomorphen Verarbeitung, die eine bessere Schätzung der Merkmale des Aufzeichnungssystems ermöglicht).