- Was ist die Steigungs-Abschnitt-Form
- Was ist b in y=mx+b?
- Was ist m in der Steigungsschnittpunktform?
- Wie schreibt man eine Gleichung in der Steigungs-Abschnitt-Form?
- Wie findet man den y-Achsenabschnitt?
- Wie findet man die Steigung einer Gleichung?
- Was ist eine undefinierte Steigung?
- Gleichung aus einem Punkt finden
- Bestimmen der Steigung aus zwei Punkten
- Gleichung einer Geraden bei zwei Punkten
- Wie findet man den Bereich und die Reichweite?
Was ist die Steigungs-Abschnitt-Form
Die Steigungs-Abschnitt-Form ist eine der drei Formen, die wir verwenden können, um eine gerade Linie auszudrücken. Die anderen Formen heißen Punkt-Steilheit-Form und Standardform, aber wir werden in diesem Abschnitt hauptsächlich die Steigungs-Abschnitts-Form verwenden. Mit der Steigungs-Abschnitts-Form drücken wir die Gleichung einer Geraden wie folgt aus:
Sie wissen vielleicht, dass xxx und yyy die Koordinaten eines Punktes in einem Diagramm sind, aber was sind mmm und bbb?
Was ist b in y=mx+b?
Der Buchstabe b ist eine Zahl, die angibt, wann die Gerade die y-Achse berührt. Wir bezeichnen dies auch als „y-Achsenabschnitt“. Zeichnen wir zum Beispiel eine Gerade auf der Koordinatenebene.
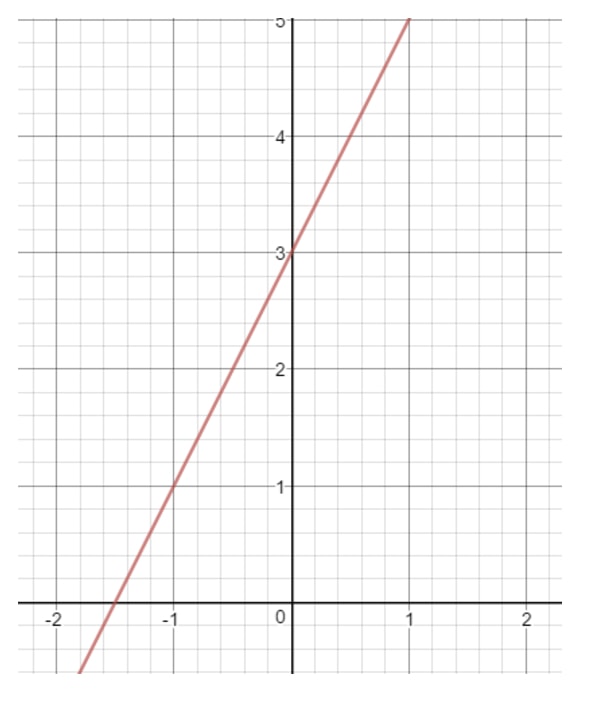
Wenn du die y-Achse genau betrachtest, berührt die Gerade die y-Achse an einer bestimmten Stelle. Wo ist diese Stelle? Das wäre die Zahl 3, denn dort schneiden sich die y-Achse und die Gerade. Daraus können wir schließen, dass b = 3 ist.
Was ist m in der Steigungsschnittpunktform?
Der Buchstabe m ist eine Zahl, die die Steigung der Geraden darstellt. Manche Leute bezeichnen die Steigung als Anstieg über dem Verlauf. Erinnern wir uns daran, dass wir, wenn wir zwei Punkte haben, die Steigung der beiden Punkte mit Hilfe der Steigungsformel
Die gleiche Idee funktioniert hier. Wenn wir zwei beliebige Punkte auf einer Geraden nehmen, dann können wir die Steigung der Geraden mit Hilfe der obigen Formel finden! Nehmen wir zum Beispiel diese Gerade:
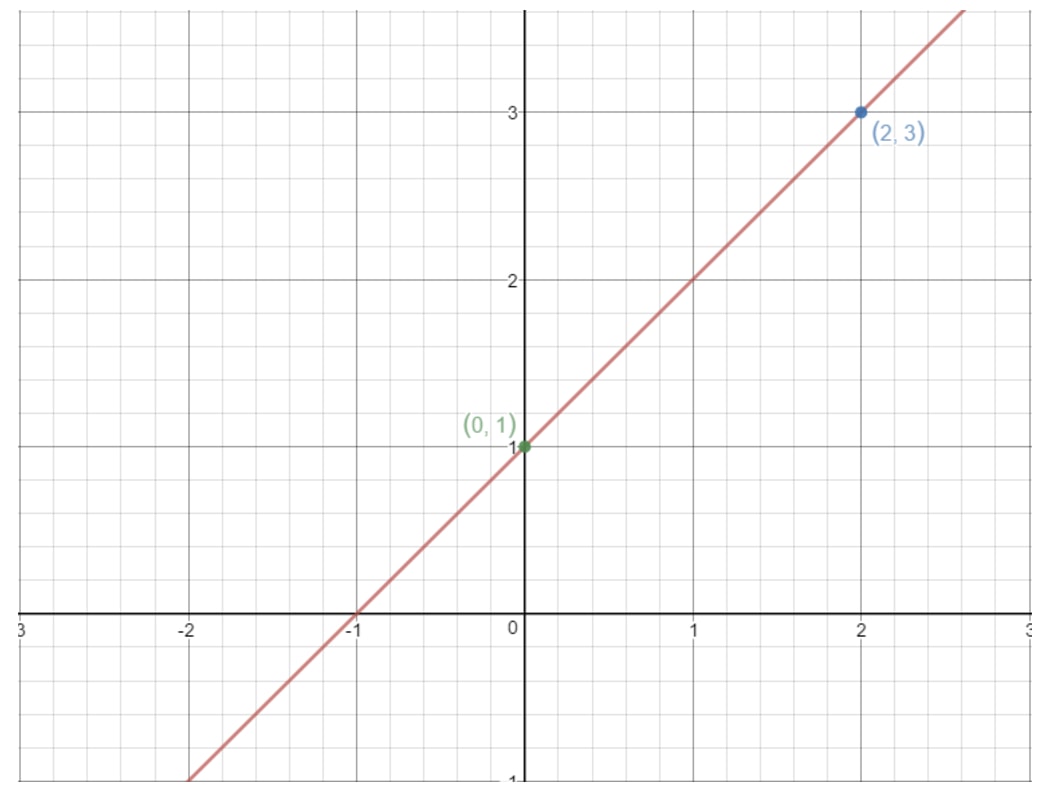
Beachten Sie, dass die Punkte (2, 3) und (0, 1) auf dieser Grafik liegen. Warum verwenden wir also nicht diese beiden Punkte, um die Steigung der Geraden zu bestimmen? Mit der Formel erhalten wir:
Das bedeutet, dass die Steigung dieser Linie 111 ist!
Das Besondere an Steigungen ist, dass wir zwei beliebige Punkte auf der Linie verwenden können, um sie zu finden. Wenn du also zwei verschiedene Punkte auf dieser Linie nimmst, erhältst du immer noch die Steigung 111.
Wie schreibt man eine Gleichung in der Steigungs-Abschnitt-Form?
Du weißt vielleicht, wie die Steigungs-Abschnitt-Form aussieht, aber die Hälfte der Zeit werden dir Gleichungen gegeben, die nicht in dieser Form vorliegen. Es ist also deine Aufgabe, sie in die Steigungs-Abschnitt-Form umzuwandeln. Wie machen wir das? Ziel ist es, den yyy-Term immer zu isolieren. Nehmen wir zum Beispiel an, du hast die Gleichung
Um yyy zu isolieren, verschieben wir 6x+46x + 46x+4 auf die rechte Seite der Gleichung
Nun ist die 222 im Weg von yyy, also werden wir sie los, indem wir beide Seiten der Gleichung durch 222 teilen.
Da yyy isoliert ist, kann man sehen, dass es in der Steigungs-Abschnitt-Form y=mx+by = mx + by=mx+b ist, wobei m=-3m = -3m=-3 und b=-2b = -2b=-2.
Nun, da wir den y-Achsenabschnitt und die Steigung sehr gut kennen, schauen wir uns doch mal konkrete Fragen an, um sie zu finden!
Wie findet man den y-Achsenabschnitt?
Frage 1: Finde den y-Achsenabschnitt anhand der linearen Gleichung y=12x+5y = \frac{1}{2} x + 5y=21x+5.
Beachte hier, dass die Gleichung bereits in der Steigungs-Abschnitt-Form y=mx+by = mx + by=mx+b vorliegt. Wir müssen nur noch herausfinden, was bbb ist. Wir sehen, dass b=5b = 5b=5 ist, also ist der y-Achsenabschnitt 555.
Lassen Sie uns eine etwas schwierigere Frage stellen.
Frage 2: Bestimmen Sie den y-Achsenabschnitt von 2x-4y=82x – 4y = 82x-4y=8
Nun liegt diese lineare Gleichung nicht in der Steigungs-Achsenabschnitt-Form vor, also müssen wir sie zuerst in diese Form umwandeln. Unser Ziel ist es, yyy in dieser Gleichung zu isolieren.
Siehst du, wenn wir 2x2x2x auf die rechte Seite der Gleichung verschieben, erhalten wir:
Nun teilen wir beide Seiten durch -4-4-4, dann erhalten wir:
Wenn man nun die Positionen der beiden Terme vertauscht, erhält man:
Frage 3: Bestimme den y-Achsenabschnitt von 4y-8=04y – 8 = 04y-8=0.
Dies sieht vielleicht etwas seltsam aus, weil es keinen xxx-Term gibt, aber unser Ziel bleibt das gleiche. Wir werden yyy isolieren.
Wenn wir die -8-8-8 auf die rechte Seite der Gleichung verschieben, erhalten wir:
Teilt man beide Seiten der Gleichung durch 444, erhält man
Nun sieht es vielleicht nicht so aus, aber die Gleichung hat die Form eines Steigungsabschnitts. Es ist nur so, dass m=0m = 0m=0, also ist der gesamte mxmxmx-Term verschwunden. Schreibe die Gleichung einfach um in
Aus der Beobachtung kannst du erkennen, dass b=2b = 2b=2 ist und der y-Abschnitt somit 222 ist. Machen wir noch eine Frage.
Frage 4: Bestimme (wenn möglich) den y-Abschnitt von 5x-15=05x – 15 = 05x-15=0.
Diese Frage ist interessant, weil die Gleichung keinen yyy-Term hat. Wie sollen wir sie also in die Form des Steigungsabschnitts bringen? Nun, das Einzige, was wir im Moment tun können, ist, für xxx zu isolieren, also versuchen wir das erst einmal.
Wenn wir die 151515 auf die rechte Seite der Gleichung verschieben, erhalten wir:
Die Division beider Seiten der Gleichung ergibt:
Nun werden wir dies in ein Diagramm zeichnen. Beachten Sie, dass xxx in dieser Gleichung zwingend 333 sein muss und nichts anderes sein kann. Sie sagt jedoch nichts über yyy aus, also kann yyy alles sein, was es will. Wenn wir eine Wertetabelle schreiben, erhalten wir:
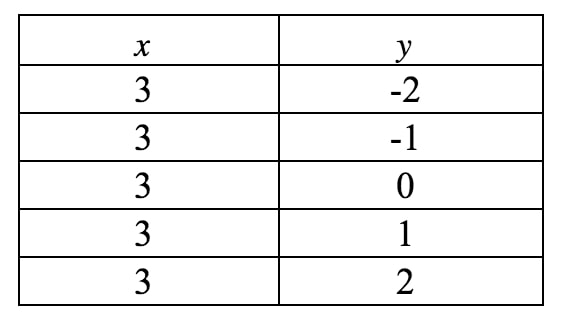
Wenn wir diese Punkte auf eine Koordinatenebene auftragen und die Linie zeichnen, erhalten wir:
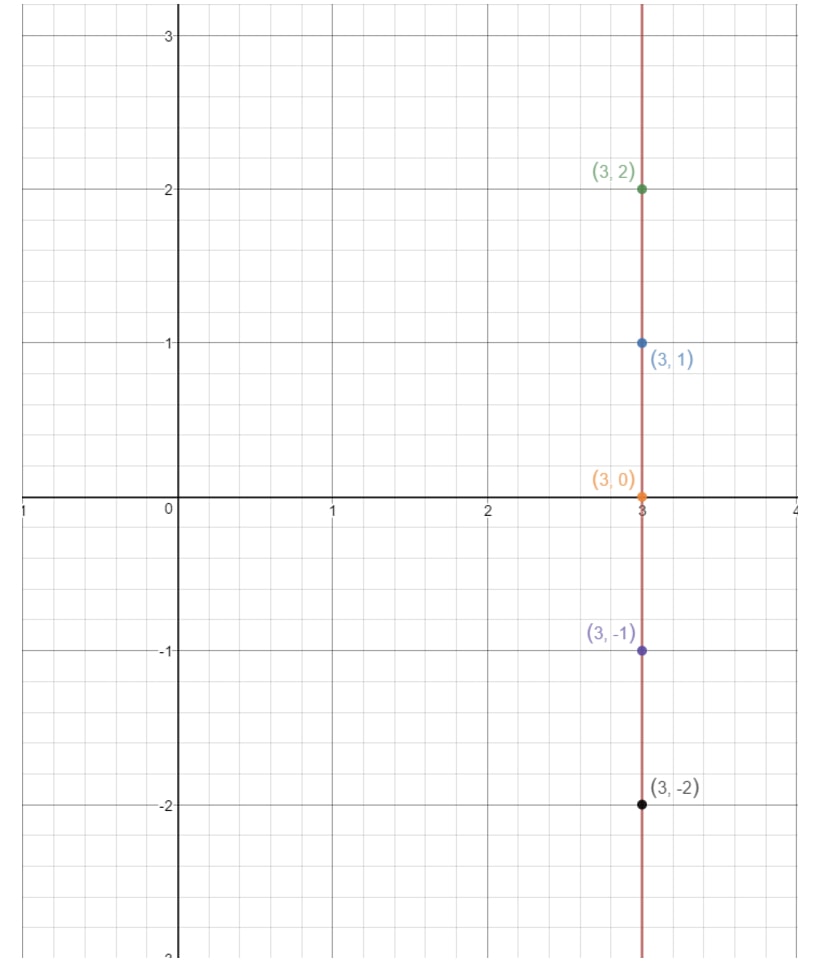
Beachten Sie, dass die Linie die y-Achse nie berührt. Das bedeutet, dass die Gleichung keinen y-Abschnitt hat. Nachdem wir nun alle Fälle, in denen der y-Achsenabschnitt gefunden werden kann, behandelt haben, wollen wir uns nun den Fragen zuwenden, bei denen es darum geht, die Steigung zu finden!
Wie findet man die Steigung einer Gleichung?
Frage 5: Finde die Steigung von y=32x+1y = \frac{3}{2}x + 1y=23x+1
Frage 6: Bestimme die Steigung der linearen Gleichung 6x-6y=06x – 6y = 06x-6y=0
Wie du siehst, liegt die Gleichung nicht in der Steigungs-Abschnitt-Form vor, also müssen wir sie zuerst in diese Form umwandeln. Unser Ziel ist es, yyy zu isolieren.
Das Verschieben von 6x6x6x auf die rechte Seite der Gleichung ergibt:
Dividieren beider Seiten durch -6-6-6 ergibt:
Beachte, dass dies eigentlich in der Steigungs-Abschnitt-Form y=mx+by = mx + by=mx+b ist. Der y-Abschnitt bbb ist in diesem Fall 000, und xxx ist gleich 1x1x1x. Wir können die Gleichung also umschreiben in:
Nun sehen wir durch Beobachtung, dass m=1m = 1m=1. Da mmm die Steigung ist, muss die Steigung 111 sein. Machen wir eine etwas schwierigere Aufgabe
Frage 7: Bestimmen Sie die Steigung von 2y-4=02y – 4 = 02y-4=0
Auch dies ist ein wenig seltsam, weil wir keinen xxx-Term haben. Unser Ziel, yyy zu isolieren, bleibt jedoch dasselbe.
Wenn man -4-4-4 auf die rechte Seite der Gleichung verschiebt, erhält man:
Dividieren beider Seiten der Gleichung durch 222 ergibt:
Sie sehen hier, dass die Gleichung nun in der Steigungs-Abschnitt-Form vorliegt, nur dass der Term mxmxmx ausgeblendet ist, weil m=0m = 0m=0. Wir können unsere Gleichung also umschreiben als:
Da m=0m = 0m=0 ist, haben wir eine Steigung von Null. Wenn du dich fragst, wie eine Linie mit der Steigung 000 aussieht, dann kannst du dir hier einen Graphen ansehen.
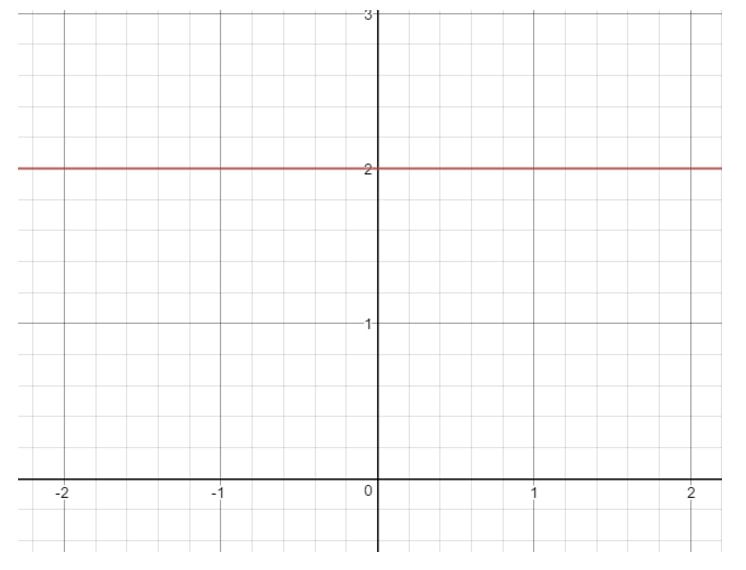
Frage 8: Finde (wenn möglich) die Steigung der linearen Gleichung 16-4x=016 – 4x = 016-4x=0
In diesem Fall kann yyy nicht isoliert werden, weil es keinen yyy-Term gibt. Das Einzige, was wir tun können, ist, xxx zu isolieren.
Das Verschieben von 161616 auf die rechte Seite der Gleichung ergibt:
Dividiert man beide Seiten durch -4-4-4, erhält man:
Dies ist immer noch nicht in Form des Steigungsabschnitts, so dass unsere einzige Hoffnung, die Steigung zu erhalten, darin besteht, einen Graphen dieser Linie zu zeichnen. Auch hier sehen wir, dass xxx immer 444 sein muss, aber yyy kann alles sein, was es will, weil es keinen yyy-Term gibt. Wenn wir eine Wertetabelle schreiben, erhalten wir:
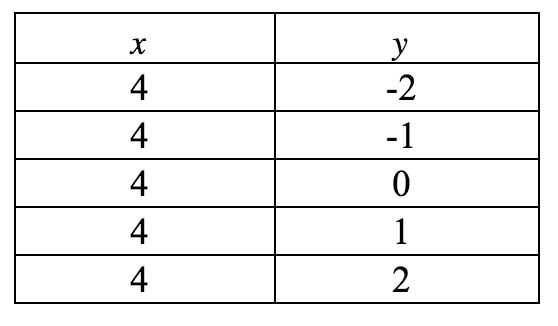
Wenn wir diese Punkte in eine Koordinatenebene einzeichnen und die Linie zeichnen, erhalten wir:
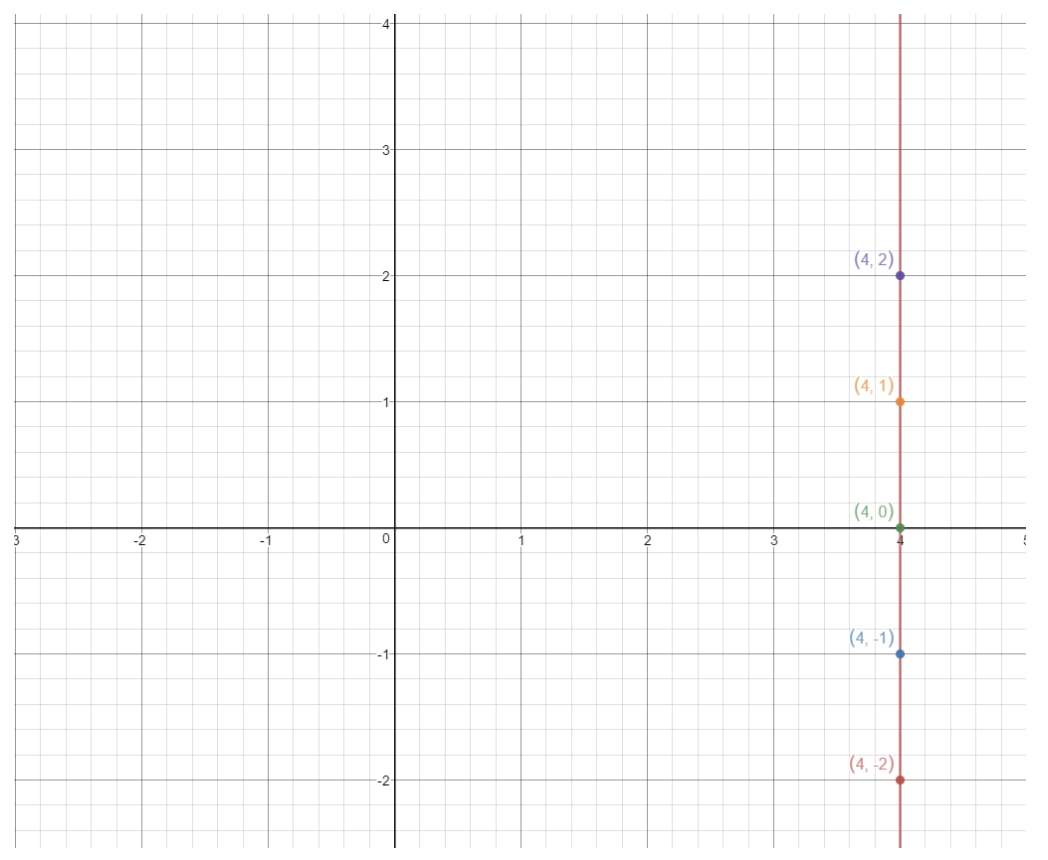
Das ist eine vertikale Linie. Was ist nun die Steigung einer vertikalen Linie? Versuchen wir, das herauszufinden, indem wir die Steigung und den Verlauf bestimmen. Sehen Sie, dass diese Linie immer unendlich ansteigt, aber es gibt überhaupt keinen Anstieg. Das bedeutet also, dass die Steigung 000 ist. Wenn wir also die Steigung berechnen, erhalten wir:
Wir können nicht durch 000 dividieren, also haben wir tatsächlich eine unbestimmte Steigung.
Was ist eine undefinierte Steigung?
Eine undefinierte Steigung ist eine Steigung, die im Diagramm gerade nach oben geht. Wie im obigen Diagramm zu sehen ist, steigt die Steigung unendlich an und hat keinen Verlauf. Als Ergebnis erhalten wir eine undefinierte Steigung, weil wir nicht durch 000 teilen können.
Im Allgemeinen erhalten wir immer eine undefinierte Steigung, wenn wir eine gerade vertikale Linie erhalten!
Lassen Sie uns einige andere einzigartige Fragen betrachten!
Gleichung aus einem Punkt finden
Frage 9: Ein Punkt (2, 6) geht durch eine Gleichung von y=-5x+by = -5x + by=-5x+b. Finde „bbb“.
Das Isolieren und Lösen von bbb ergibt:
Erinnern Sie sich daran, dass bbb auch als y-Achsenabschnitt bekannt ist, also ist der y-Achsenabschnitt auch 161616!
Bestimmen der Steigung aus zwei Punkten
Frage 10: Bestimmen Sie die Steigung der Geraden aus zwei Punkten (6, 1) und (-10, 9).
Erinnern Sie sich daran, dass wir die Steigung der Geraden mit der Steigungsgleichung
Die Anwendung dieser Formel ergibt also:
Was, wenn wir stattdessen die gesamte Gleichung einer Geraden finden sollen?
Gleichung einer Geraden bei zwei Punkten
Frage 11: Finden Sie bei zwei Punkten (-6, 1) und (2, 6) die Gleichung in Form der Steigung und des Achsenabschnitts.
Wir versuchen grundsätzlich, die Gleichung in der Form y=mx+by = mx + by=mx+b zu finden. Um dies zu tun, müssen wir nach mmm und bbb suchen.
Erinnern Sie sich, dass wir, um mmm zu finden, die Steigungsgleichung
Die Anwendung dieser Formel ergibt also:
Also haben wir jetzt die Gleichung
Nun müssen wir nach bbb suchen. Um bbb zu lösen, wählen wir einen der beiden gegebenen Punkte und setzen ihn in die Gleichung ein. Das ist möglich, weil beide Punkte auf der Geraden liegen und jeder Punkt auf der Geraden die Gleichung erfüllen würde. Wir verwenden den Punkt (2, 6). Wir sehen, dass:
Das Isolieren von bbb ergibt:
In dezimaler Form ausgedrückt, ergibt sich b=4,75b = 4,75b=4,75. Daher lautet unsere Gleichung in Form des Steigungsabschnitts:
Das letzte, was wir in diesem Abschnitt behandeln, ist das Finden des Bereichs und der Reichweite einer Linie.
Wie findet man den Bereich und die Reichweite?
Um den Bereich einer Linie zu finden, stellen wir uns im Grunde die folgende Frage: Was kann xxx sein? Wenn xxx diese Werte sein können, dann fügen wir sie zum Bereich hinzu.
Das Gleiche gilt für den Bereich. Was kann yyy sein? Wenn yyy diese Werte sein können, dann fügen wir sie in den Bereich ein. Machen wir ein Beispiel.
Frage 12: Finde die Domäne und den Bereich der Gleichung y=2x+1y = 2x + 1y=2x+1.
Beachte, dass wir, wenn wir den Graphen dieser Linie zeichnen, folgendes erhalten:
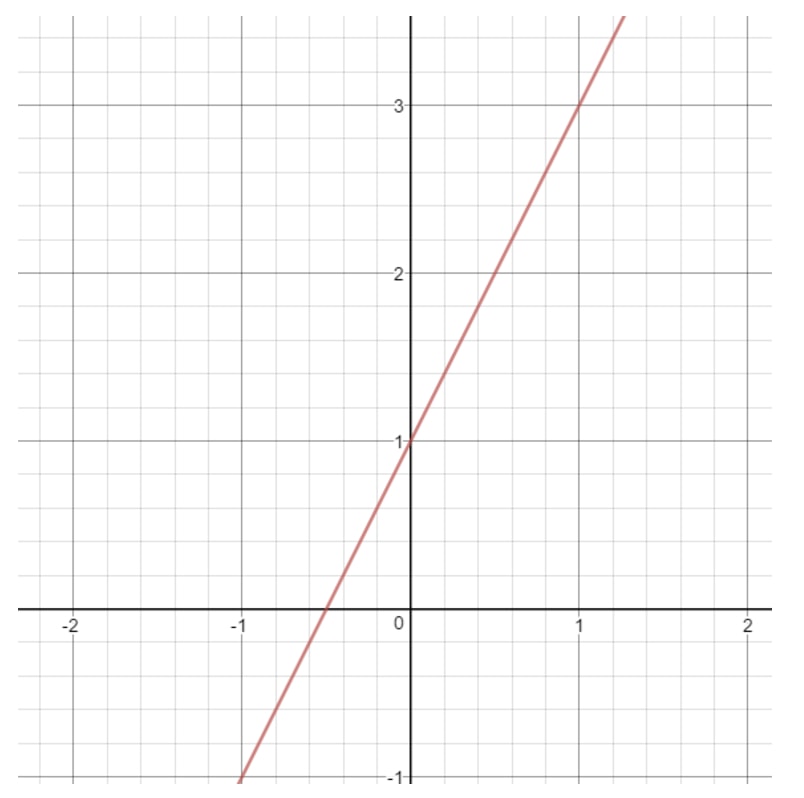
Was kann xxx in dieser Linie sein? Beachten Sie, dass xxx alles sein kann, weil wir mit jedem xxx-Wert einen Punkt auf der Linie erhalten können. Dasselbe gilt für y. Wir können immer einen yyy-Wert wählen, der uns einen Punkt auf einer Linie liefert. Wir sagen also, dass
wobei R „alle reellen Zahlen“ bedeutet. Machen wir eine schwierigere Aufgabe.
Frage 13: Finde den Bereich und den Umfang der Gleichung y=-2y = -2y=-2.
Wenn wir nun diese Linie in ein Diagramm einzeichnen, erhalten wir:
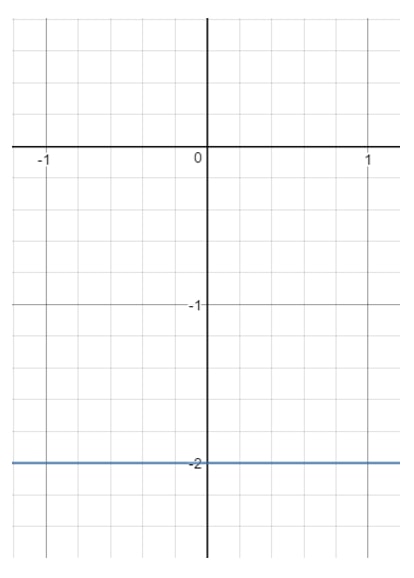
Beachte, dass xxx alles sein kann, denn mit jedem xxx-Wert können wir einen Punkt erhalten, der auf der Linie liegt, solange y=-2y = -2y=-2. Betrachten Sie jedoch yyy. Sie sehen, dass yyy zu -2-2-2 gezwungen ist und nichts anderes sein kann. In dem Moment, in dem Sie einen anderen Wert für yyy wählen (z. B. 111), liegt der Punkt nicht mehr auf der Geraden. Das bedeutet also:
Frage 14: Finde das Gebiet und den Bereich der Gleichung x=1x = 1x=1.
Wenn wir nun diese Linie in einen Graphen zeichnen, erhalten wir:
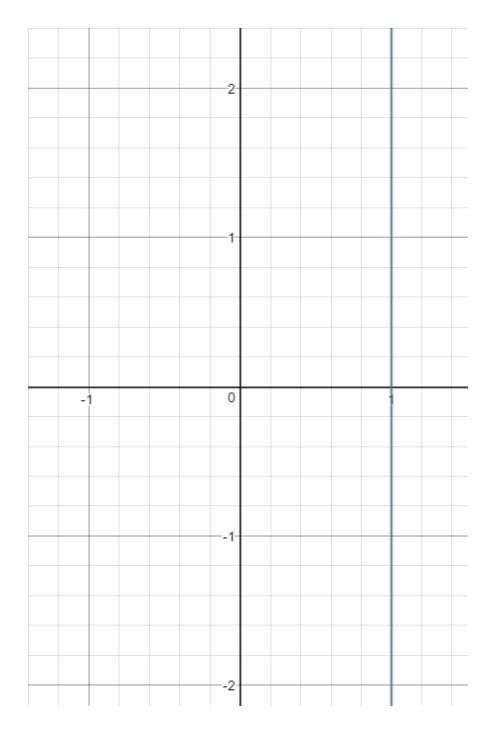
Du siehst, dass xxx auf 111 gezwungen ist und nichts anderes sein kann. In dem Moment, in dem du einen anderen Wert für xxx wählst (z.B. 222), wird dieser Punkt außerhalb der Linie liegen, aber sieh dir yyy an. Beachte, dass yyy alles sein kann, denn mit jedem yyy-Wert können wir einen Punkt erhalten, der auf der Linie liegt, solange x=1x = 1x=1
Das bedeutet also:
Wenn du viele Probleme hattest, die Graphen zu zeichnen, um die Domäne und den Bereich zu erhalten, empfehle ich dir, diesen Rechner zu benutzen.
https://www.desmos.com/calculator/2rnqgoa6a4
Er lehrt dich, wie man eine lineare Gleichung grafisch darstellt. Du brauchst nur die Werte von mmm und bbb einzugeben. Dann wird die Linie automatisch für dich gezeichnet! Das ist auch nützlich, wenn du versuchst, die Steigungs-Abschnitt-Form zu finden.