Wie berechnet man die Spannung in Seilen, an denen ein Objekt aufgehängt ist

In der Abbildung unten sehen wir, dass die Kraft F, die zum Anheben des Objekts benötigt wird, gleich dem Gewicht W des Objekts ist. Diese Idee ist das grundlegende Konzept, das unserer Formel für die Zugkraft zugrunde liegt. Ebenfalls unten abgebildet ist das Freikörperdiagramm des Objekts, das die in der Schnur wirkenden Spannungskräfte T zeigt. Wie Sie sehen können, treten die Spannungskräfte paarweise und in entgegengesetzten Richtungen auf:

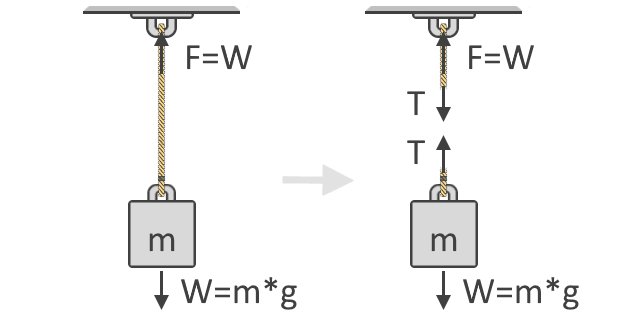
Nach Newtons zweitem Bewegungsgesetz können wir die Summe der Kräfte mit Hilfe des Freikörperdiagramms des Objekts ausdrücken, wie auf der rechten Seite der obigen Abbildung dargestellt. Wir verwenden Freikörper-Diagramme, um die verschiedenen Richtungen und Größen der Kräfte darzustellen, die auf einen Körper wirken. Im Gleichgewicht sollten diese Kräfte alle gleich Null sein. Wenn wir alle nach oben gerichteten Kräfte als positiv und alle nach unten gerichteten als negativ betrachten, lautet unsere Gleichung:

ΣF = 0 = T + (-W)
T = W
wobei das Gewicht W negativ wird, da es nach unten gerichtet ist. Wenn wir W auf die andere Seite der Gleichung übertragen, können wir sehen, dass die Zugkraft im Seil gleich dem Gewicht des Objekts ist, das es trägt, wie oben gezeigt.

Wenn wir mehrere Seile verwenden, um das Objekt zu heben, wird die gesamte Zugkraft auf die Seile aufgeteilt. Die Zugkraft in den einzelnen Seilen hängt von ihrem Winkel zur Richtung der Kraft ab, der sie entgegenwirken. Um dies besser zu verstehen, betrachten wir ein weiteres Freikörper-Diagramm eines an zwei Seilen aufgehängten Objekts, wie unten gezeigt:

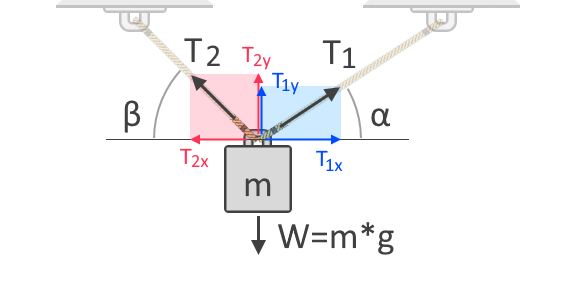
In dem oben gezeigten Freikörper-Diagramm können wir die horizontalen und vertikalen Komponenten der Spannungskräfte, T₁ und T₂, sehen. Kräfte sind Vektoren, d. h. sie haben immer sowohl einen Betrag als auch eine Richtung. Wie alle Vektoren können Kräfte in diesen Komponenten ausgedrückt werden, die den Einfluss der Kraft entlang der horizontalen und vertikalen Achsen angeben. T₁ₓ und T₂ₓ sind die vertikalen Komponenten von T₁ bzw. T₂. Andererseits sind T₁ᵧ und T₂ᵧ die vertikalen Komponenten der gleichen Kräfte. Da die Schwerkraft auf das Objekt in der vertikalen Achse wirkt, müssen wir die vertikalen Komponenten der Spannungskräfte bei unserer Kräftesummierung wie folgt berücksichtigen:

ΣF = 0 = T₁ᵧ + T₂ᵧ + (-W)
W = T₁ᵧ + T₂ᵧ

Da wir auch die Winkel der Zugkräfte kennen, können wir T₁ᵧ und T₂ᵧ mit Hilfe von trigonometrischen Funktionen in T₁ bzw. T₂ ausdrücken:

T₁ᵧ = T₁ * sin(α)
T₂ᵧ = T₂ * sin(β)
W = T₁ * sin(α) + T₂ * sin(β)

Wir können auch sagen, dass sich das Objekt nicht horizontal oder entlang der x-Achse bewegen sollte, damit das System im Gleichgewicht ist. Daher müssen die horizontalen Komponenten von T₁ und T₂ dann gleich Null sein. Außerdem können wir mit Hilfe der Trigonometrie T₁ₓ und T₂ₓ in Form von T₁ bzw. T₂ ausdrücken:

T₁ₓ = T₂ₓ
T₁ * cos(α) = T₂ * cos(β)

Wenn wir beide Seiten durch cos(α) dividieren, erhalten wir eine Gleichung, in der T₁ in Form von T₂ und den Winkeln ausgedrückt wird:

T₁ = T₂ * cos(β) / cos(α)

Wir können diese Gleichung dann verwenden, um T₂ zu lösen, indem wir T₂ * cos(β) / cos(α) als T₁ in unsere Gleichung zur Addition der Kräfte einsetzen, wie unten gezeigt:

W = T₁ * sin(α) + T₂ * sin(β)
W = T₂ * * sin(α) + T₂ * sin(β)
W = T₂ *
T₂ = W /

Wenn wir schließlich diese gesamte Gleichung mit cos(β) / cos(α) multiplizieren, wie wir den Wert von T₁ in Bezug auf T₂ abgeleitet haben, und dann alles vereinfachen, erhalten wir diese Gleichung:

T₁ = W / *
T₁ = W / *
T₁ = W /

Nun muss man nur noch die Winkel der Zugseile zur Horizontalen kennen. Ist ein Winkel zur Senkrechten angegeben, so subtrahieren Sie diesen Winkel einfach von 90°. Auf diese Weise erhält man den Winkel zur Horizontalen. Wenn Sie jedoch andere Winkelwerte erhalten, die größer als 90° oder sogar 180° sein können, sollten Sie unseren Referenzwinkelrechner zu Rate ziehen, um den benötigten Winkel zu ermitteln. Nachdem wir die Werte für die Variablen in unseren Spannkraftformeln bestimmt haben, können wir nun die Spannkräfte berechnen.