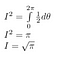Lord Kelvin schrieb über dieses Integral: „Ein Mathematiker ist jemand, für den das so offensichtlich ist, wie für dich, dass zweimal zwei vier ergibt.“
Viel Spaß 😉
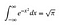
OK, ich gehe also davon aus, dass du ein paar Grundkenntnisse in Integration und Differenzierung hast. Im Folgenden werden die cleveren Tricks, die später kommen, etwas intuitiver. Machen Sie sich keine Sorgen, wenn einiges davon etwas verwirrend ist, versuchen Sie einfach, ein Gefühl dafür zu bekommen, was passiert.
Die Strategie hier wird sein, eine clevere Substitution durchzuführen. Aber wir werden eine Substitution in zwei Variablen durchführen. Du kannst dir das aktuelle Problem als Berechnung der Fläche unter einer Kurve vorstellen
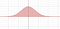
Aber wir werden zeigen, dass das Problem in eine Volumenberechnung umgewandelt werden kann.
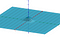
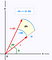
Um das Volumen zu berechnen, verwenden wir eine etwas andere Formel für den Variablenwechsel als bei normalen Integralen. Wir werden Polarkoordinaten verwenden. Dabei werden die x- und y-Koordinaten durch ihren Radius und ihren Winkel ausgedrückt. Geogebra bietet hier eine schöne interaktive Darstellung

Dann verwenden wir die magische Basiswechselformel für Polarkoordinaten.
Bei der Berechnung der Fläche unter der Kurve hatten wir das Element ‚dx‘, das einen kleinen Abstand entlang der x-Achse darstellt. Bei der Berechnung eines Volumens haben wir dx dy, das wie ein kleines Rechteck mit den Seitenlängen dx und dy ist. Mit diesen Basen erstellen wir dann eine Reihe von Kästchen, die das Volumen schätzen. Dies lässt sich am einfachsten mit der nachstehenden Visualisierung veranschaulichen. Das Integral ist der Grenzwert dieser Näherungen.
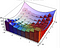
Wenn wir stattdessen das Polarkoordinatensystem verwenden, haben wir ein etwas anderes Flächenelement darunter. Unten ist dA das Flächenelement. Mit kleinen Änderungen des Winkels und des Radius lässt sich dieses Flächenelement immer besser durch ein Rechteck mit den Seitenlängen dr bzw. r*dtheta approximieren. Wenn du dich mit etwas Geometrie auskennst, wird für kleine theta sin(theta) sehr gut durch theta angenähert und du kannst dann das folgende Ergebnis beweisen.
Lösen des Integrals
Zuerst geben wir unserem Integral einen Namen. Wir nennen es I.
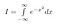
Beachte, dass x nur eine „Dummy-Variable“ ist. Der Bereich existiert unabhängig davon, welchen Variablennamen wir verwenden. Wir können also auch die folgenden zwei Gleichungen schreiben
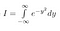
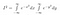
Nun, da I nur eine Konstante ist, deren Wert wir noch nicht kennen, können wir unsere normalen Regeln anwenden, um eine Konstante in ein Integral zu bringen
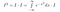
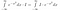
So weit haben wir noch nicht viel Substantielles gemacht. Jetzt denken wir intensiv darüber nach, was das Integral bedeutet. Wir nehmen Integrale von Funktionen. Wenn zwei Funktionen überall den gleichen Wert annehmen, sind sie gleich groß und haben den gleichen Flächeninhalt. In diesem Sinne können wir die folgenden Manipulationen vornehmen, wenn wir I*exp(-x²) als eine Funktion von x betrachten, d.h. als etwas, das Werte von x als Eingabe annimmt und eine Zahl als Ausgabe liefert.
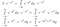
Ok, das war eine Menge zu verkraften. In der ersten Zeile haben wir einfach I in seiner Integralform mit einem anderen Variablennamen neu geschrieben. In der zweiten Zeile, in der wir I*exp(-x²) als Funktion behandelten, stellten wir fest, dass wir exp(-x²) in das dy-Integral einfügen können, was immer noch den gleichen Ausgabewert für jeden Eingabewert von x ergeben würde. Schließlich haben wir die Regeln der Potenzierung angewandt.
Wenn wir dies vollständig ausschreiben, haben wir nun
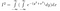
Nun kommt die entscheidende Erkenntnis. Oben haben wir mit Variablennamen herumgespielt und damit, wie man eine Funktion darstellt. Jetzt wechseln wir die Perspektive: Dieser Ausdruck stellt auch das Integral von exp(-(y²+x²)) über die gesamte 2D-Ebene dar, mit dem Flächenelement dA = dx dy. D.h. dx dy ist ein kleines Rechteck in der Ebene, und exp(-(y²+x²)) ist die Höhe über diesem Rechteck.
Als Nächstes verwenden wir die Polarkoordinatenerkenntnisse von vorhin
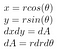
Als sin² + cos² = 1, nachdem wir alles eingesteckt haben, erhalten wir
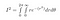
r reicht von 0 bis unendlich und theta reicht von 0 bis 2*pi, da dies die gesamte 2D-Ebene abdeckt: Jeder Punkt hat einen Radius, der kleiner als unendlich ist, und einen Winkel zwischen 0 und 2*pi Radiant.
Wir können das innere Integral mit Hilfe der Kettenregel auswerten
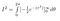
Und, im gelobten Land befinden wir uns nun: