von Marco Taboga, PhD
Die Indikatorfunktion eines Ereignisses ist eine Zufallsvariable, die den Wert 1 annimmt, wenn das Ereignis eintritt und den Wert 0, wenn das Ereignis nicht eintritt. Indikatorfunktionen werden in der Wahrscheinlichkeitstheorie häufig verwendet, um die Notation zu vereinfachen und Theoreme zu beweisen.
Definition
Es folgt eine formale Definition.
Definition Sei 
ein Stichprobenraum und ein Ereignis. Die Indikatorfunktion (oder Indikator-Zufallsvariable) des Ereignisses , bezeichnet mit , ist eine wie folgt definierte Zufallsvariable: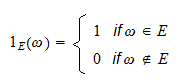
Während der Indikator eines Ereignisses gewöhnlich durch bezeichnet wird, wird er manchmal auch durch bezeichnet, wobei der griechische Buchstabe Chi ist.
Beispiel Wir werfen einen Würfel und eine der sechs Zahlen von 1 bis 6 kann aufgedeckt werden. Der Probenraum istBestimmen Sie das Ereignis , das durch den Satz „Eine gerade Zahl erscheint mit dem Bild nach oben“ beschrieben wird. Eine Zufallsvariable, die den Wert 1 annimmt, wenn eine gerade Zahl mit dem Bild nach oben erscheint, und ansonsten den Wert 0, ist ein Indikator für das Ereignis . Die fallweise Definition dieses Indikators lautet
Aus der obigen Definition lässt sich leicht erkennen, dass eine diskrete Zufallsvariable mit Unterstützung und Wahrscheinlichkeitsmassenfunktion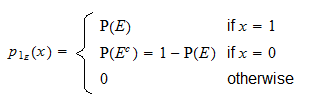
Eigenschaften
Indikatorfunktionen haben die folgenden Eigenschaften.
Potenzen
Die -te Potenz von ist gleich :weil entweder oder sein kann und
Erwartungswert
Der Erwartungswert von ist gleich :
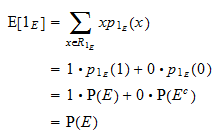
Varianz
Die Varianz von ist gleich . Dank der üblichen Varianzformel und der obigen Potenzeigenschaft erhalten wir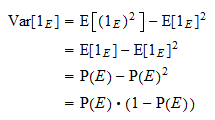
Schnittmengen
Wenn und zwei Ereignisse sind, dannsind:
-
wenn
, dann und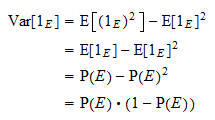
-
wenn
, dannund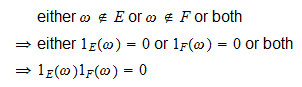
Indikatoren für Ereignisse mit Nullwahrscheinlichkeit
Sei ein Ereignis mit Nullwahrscheinlichkeit und eine ganzzahlige Zufallsvariable. Dann Während ein strenger Beweis dieser Tatsache den Rahmen dieser einführenden Darstellung sprengen würde, sollte diese Eigenschaft intuitiv sein. Die Zufallsvariable ist für alle Stichprobenpunkte gleich Null, außer möglicherweise für die Punkte . Der Erwartungswert ist ein gewichteter Durchschnitt der Werte, die annehmen kann, wobei jeder Wert mit seiner jeweiligen Wahrscheinlichkeit gewichtet wird. Die von Null verschiedenen Werte, die annehmen kann, werden mit Wahrscheinlichkeiten von Null gewichtet, so dass Null sein muss.
Gelöste Aufgaben
Nachfolgend finden Sie einige Aufgaben mit erklärten Lösungen.
Übung 1
Betrachte eine Zufallsvariable und eine weitere Zufallsvariable , die als Funktion von definiert ist.
Drücke mit Hilfe der Indikatorfunktionen der Ereignisse und aus.
Bezeichne mit den Indikator des Ereignisses und bezeichne mit den Indikator des Ereignisses . Wir können schreiben als
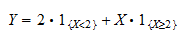
Übung 2
Sei eine positive Zufallsvariable, das heißt eine Zufallsvariable, die nur positive Werte annehmen kann. Sei eine Konstante. Beweisen Sie, dass wobei der Indikator für das Ereignis ist.
Stellen Sie zunächst fest, dass die Summe der Indikatoren und immer gleich ist:Daher können wir schreiben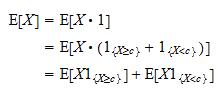
Nun stellen Sie fest, dass eine positive Zufallsvariable ist und dass der Erwartungswert einer positiven Zufallsvariablen positiv ist:Deshalb,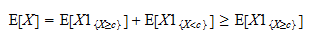
Übung 3
Sei ein Ereignis und bezeichne seine Indikatorfunktion mit . Sei das Komplement von und bezeichne seine Indikatorfunktion mit . Kannst du als Funktion von ausdrücken?
Die Summe der beiden Indikatoren ist immer gleich :Daher,
Zitierweise
Bitte zitieren als:
Taboga, Marco (2017). „Indikatorfunktionen“, Vorlesungen über Wahrscheinlichkeitstheorie und mathematische Statistik, Dritte Auflage. Kindle Direct Publishing. Online Appendix. https://www.statlect.com/fundamentals-of-probability/indicator-functions.