Wie führt man eine Guinier-Anpassung durch?¶
Die Guinier-Annäherung gilt nur, wenn das Exponential \(\exp(-q^2 R_g^2 /3)\)klein ist. Das bedeutet, dass wir für eine gute Guinier-AnnäherungqRg ausreichend klein sein müssen. Der qRg-Wert, bei dem die Guinier-Annäherung für ein bestimmtes Streuprofil zu versagen beginnt, hängt von der Gesamtform des Streuers ab. Die folgende Abbildung zeigt die Guinier-Näherung (schwarz) und die Streuintensität für eine Kugel, einen dünnen Stab und eine dünne Scheibe (alle mit demselben Rg).
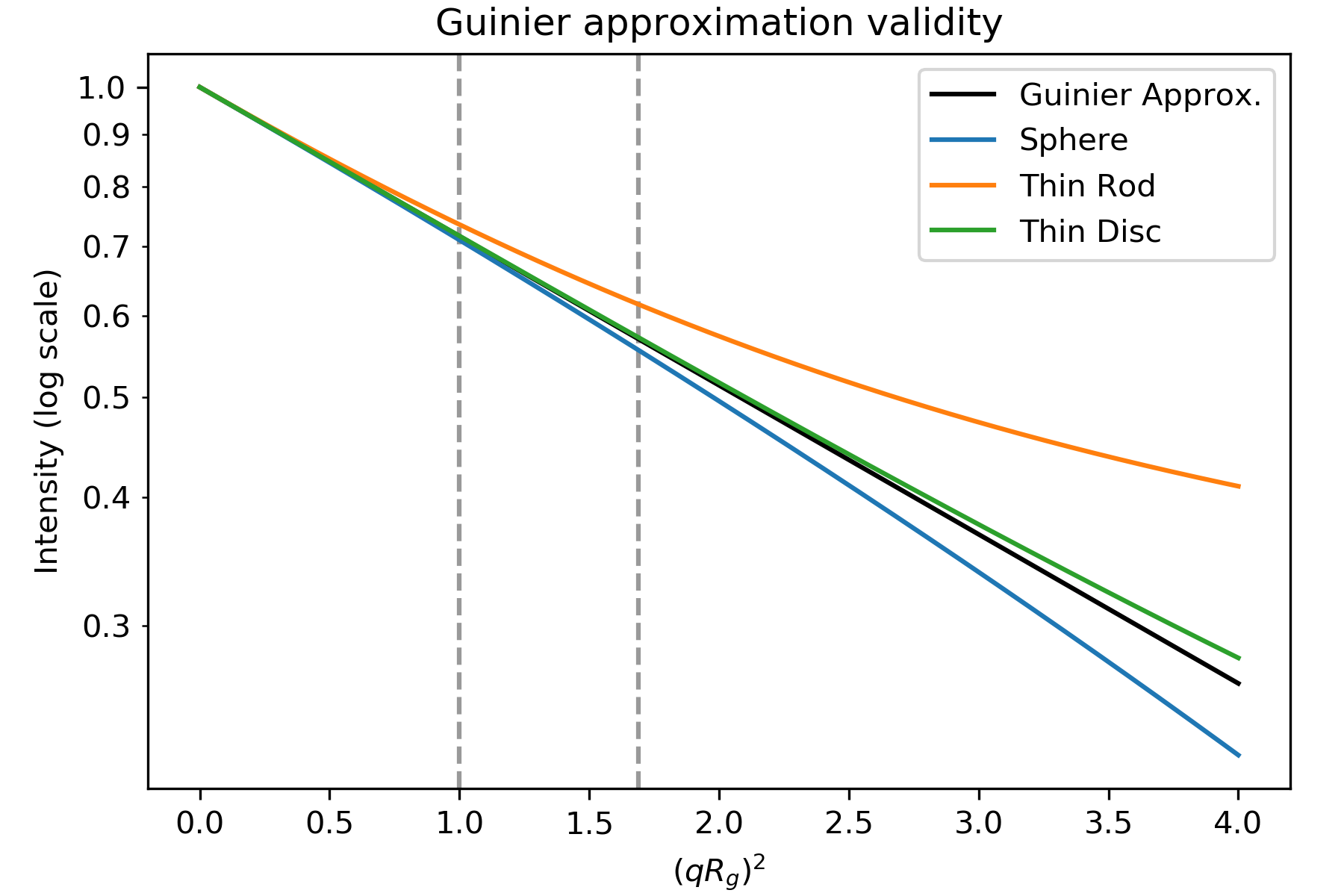
Die Darstellung basiert auf Abbildung 3.3 in . Intensität für die geometrischen Formen aus Tabelle 3.4 in . Gestrichelte Linien liegen bei qRg von 1,0 und 1,3((qRg) 2 von 1,0 und 1,69).
Wie man sieht, stimmt die Streuintensität für den Stab nur bis \(qR_g\sim 1,0\), die Kugel bis \(qR_g\sim 1,3\) und die Scheibe bis \(qR_g\sim 1,7\) mit der Guinier-Näherung überein. Je nach der Gesamtform der Partikel sollten Sie also unterschiedliche Mengen der Daten mit niedrigem q anpassen, um eine gute Guinier-Anpassung zu erhalten. (Hinweis: Die x-Achse des Diagramms ist (qRg) 2, so dass \(qR_g\sim 1,3\) als gestrichelte Linie bei 1,69 erscheint)
In der Praxis passen wir sowohl kugelförmige (kugel- und scheibenförmige) Objekte bis \(qR_g\sim 1,3\) an, während wir stark ausgedehnte (stabförmige) Objekte bis \(qR_g\sim 1,0\) anpassen. Diese Werte wurden so gewählt, dass sie einen Fehler von <10 % aufweisen, der sich aus der Abweichung der tatsächlichen Form von der Guinier-Näherung ergibt. Der Grund, warum wir eine so große Abweichung in Kauf nehmen, ist, dass die Unsicherheit auch dadurch entsteht, dass man weniger Punkte in den Daten anpasst.
Der Bereich der Guinier-Anpassung reicht also idealerweise vom frühesten verfügbaren q-Wert bis zu einem maximalen qRg von 1,0 oder 1,3. Wie bestimmt man aber, da Rg aus dem Guinier-Fit abgeleitet wird, den richtigen maximalen q-Wert für das Ende des Fits? Die Antwort ist, dass die Guinier-Anpassung iterativ durchgeführt wird:
- Bestimmen Sie einen maximalen q-Startwert für die Anpassung.
- Berechnen Sie die Guinier-Anpassung und erhalten Sie Rg.
- Wenn qmaxRg > 1,3 (oder 1,0), verringern Sie das maximale q. WennqmaxRg < 1,3 (oder 1,0), erhöhen Sie das maximale q.
- Wiederholen Sie die Schritte 2 und 3, bis Sie zu einem endgültigen maximalen q konvergieren.
Die meisten Softwareprogramme übernehmen heutzutage diese iterative Suche für Sie und liefern Ihnen bei Daten guter Qualität einen vernünftigen maximalen q-Wert, der möglicherweise nur noch ein wenig manuell verfeinert werden muss.
Der minimale q-Wert einer Guinier-Anpassung wird in der Regel durch den minimalen verfügbaren q-Wert in Ihren Daten bestimmt, der durch das Gerät, mit dem Sie die Messung durchführen, festgelegt wird.
Es ist jedoch wichtig, dass das minimale q klein genug ist, um einen vernünftigen Bereich für die Guinier-Anpassung zu erhalten. In der Regel sollte der Mindestwert für qRg bei 0,65 liegen, bei kugelförmigen Systemen kann jedoch auch ein Wert von 1,0 zulässig sein. Dies bedeutet, dass der erforderliche Mindestwert für q von der Größe des gemessenen Systems abhängt. In einigen Fällen, bei besonders großen Systemen, müssen Sie möglicherweise bewusst nach einem Instrument suchen, das bis zu einem ausreichend niedrigen q-Wert messen kann.
Wenn Ihre Daten bei niedrigem q-Wert Qualitätsprobleme aufweisen, die durch die oben aufgeführten Probleme verursacht werden können, werden Sie möglicherweise feststellen, dass der Ausschluss dieser Daten aus der Anpassung die Qualität der Anpassung verbessern kann. Dies kann zwar akzeptabel sein, doch sollten Sie dabei mit Vorsicht vorgehen und immer den gesamten Datenbereich in den Diagrammen anzeigen.Der akzeptabelste Fall ist, wenn die ersten paar Punkte entweder zu hoch oder zu niedrig sind, der Rest des Bereichs jedoch perfekt passt (siehe unten für Kriterien für eine gute Anpassung). In diesem Fall kann es sein, dass die Punkte, die am nächsten am Strahlenstop liegen, eine schlechte Statistik oder eine stärkere instrumentelle Hintergrundstreuung aufweisen und in der Regel sicher ignoriert werden können.