Zufallsereignisse, die sich in einem kontinuierlichen Stichprobenraum abspielen, können aus mindestens zwei Gründen geometrische Bilder hervorrufen: aufgrund der Art des Problems oder aufgrund der Art der Lösung.

Einige Probleme, wie Buffons Nadel, Vögel auf einem Draht, Bertrands Paradoxon oder das Problem des in drei Teile zerbrochenen Stocks, ergeben sich aufgrund ihrer Natur in einem geometrischen Rahmen. Das letztgenannte Problem lässt auch mehrere Umformulierungen zu, die einen Vergleich der Flächen von geometrischen Figuren erfordern. Im Allgemeinen kann man sich geometrische Wahrscheinlichkeiten als nichtnegative Größen (nicht größer als 1) vorstellen, die Teilbereichen eines gegebenen Gebiets nach bestimmten Regeln zugeordnet werden. Wenn die Funktion μ ein Ausdruck dieser Zuordnung ist, die auf einem Gebiet D definiert ist, dann verlangen wir zum Beispiel

0 ≤ μ(A) ≤ 1, A ⊂ D und
μ(D) = 1

Die Funktion μ ist normalerweise nicht für alle A ⊂ D definiert. Die Teilmengen von D, für die μ definiert ist, sind die Zufallsereignisse, die einen bestimmten Stichprobenraum bilden. Sehr oft wird μ durch das Verhältnis von Flächen definiert, so dass man, wenn σ(A) als „Fläche“ der Menge A definiert ist, μ(A) = σ(A) / σ(D) setzen kann.

Problem 1

Zwei Freunde, die von derselben Station aus mit der U-Bahn zu ihren Arbeitsplätzen fahren, kommen gleichmäßig zufällig zwischen 7 und 7:20 Uhr morgens an der Station an. Sie sind bereit, 5 Minuten aufeinander zu warten, und nehmen dann einen Zug, entweder gemeinsam oder allein. Wie groß ist die Wahrscheinlichkeit, dass sie sich am Bahnhof treffen?

In einem kartesischen Koordinatensystem (s, t) stellt ein Quadrat mit der Seitenlänge 20 (Minuten) alle Möglichkeiten der morgendlichen Ankunft der beiden Freunde an der U-Bahn-Station dar.

Die graue Fläche A wird durch zwei Geraden t = s + 5 und t = s – 5 begrenzt, so dass innerhalb von A |s – t| ≤ 5 ist. Daraus folgt, dass sich die beiden Freunde nur treffen, wenn ihre Ankunftszeiten s und t in den Bereich A fallen. Die Wahrscheinlichkeit dafür ergibt sich aus dem Verhältnis der Fläche von A zur Fläche des Quadrats:

/ 400 = 175/400 = 7/16.

Problem 2

(.)

Drei Punkte A, B, C liegen zufällig auf einem Kreis mit Radius 1. Wie groß ist die Wahrscheinlichkeit, dass ΔABC spitz ist?

Fixieren Sie den Punkt C. Die Positionen der Punkte A und B werden dann durch Bögen α und β definiert, die von C in zwei Richtungen ausgehen. A priori wissen wir, dass 0 < α + β < 2π. Die für unser Problem günstigen Werte von α und β (als subtendierende spitze Winkel) erfüllen 0 < α < π und 0 < β < π. Ihre Summe kann nicht kleiner als π sein, da dies den Winkel C stumpf machen würde, also α + β > π. Die Situation ist im folgenden Diagramm dargestellt, in dem das Quadrat die Seite 2π hat.

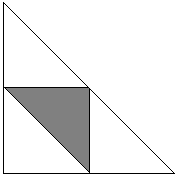
Die Region D ist der Schnittpunkt von drei Halbebenen: 0 < α, 0 < β und α + β < 2π. Dies ist das große Dreieck im obigen Diagramm. Die günstigen Ereignisse gehören zu dem schattierten Dreieck, das den Schnittpunkt der Halbebenen α < π, β < π und α + β > π bildet. Das Verhältnis der Flächen der beiden ist offensichtlich 1/4.

Wenn das zufällige Dreieck nicht spitz ist, kann es als stumpf angesehen werden, denn die Wahrscheinlichkeit, dass zwei der drei Punkte A, B, C einen Durchmesser bilden, ist 0. (Damit BC ein Durchmesser ist, müsste α + β = π sein, was eine Gerade ist, mit Null als einziger möglicher Zuordnung des Flächeninhalts.) Wir können also sagen, dass die Wahrscheinlichkeit, dass ΔABC stumpf ist, 3/4 beträgt. Bei einem stumpfen Dreieck kann der Kreis in zwei Hälften geteilt werden, wobei das Dreieck vollständig in einer der Hälften liegt. Daraus folgt, dass 3/4 die Antwort auf die folgende Frage ist:

Drei Punkte A, B, C sind zufällig auf einem Kreis mit Radius 1 angeordnet. Wie groß ist die Wahrscheinlichkeit, dass alle drei auf einem Halbkreis liegen?

1. E. J. Barbeau, Murray S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges by (MAA, 1995, Problem 244.)
2. D. A. Klain, G.-C. Rota Introduction to Geometric Probability, Cambridge University Press, 1997
3. A. A. Sveshnikov, Problems in Probability Theory, Mathematical Statistics and Theory of Random Functions, Dover, 1978
4. A. M. Yaglom, I. M. Yaglom, Challenging Mathematical Problems With Elementary Solutions, Dover, 1987

Geometrische Wahrscheinlichkeit

• Geometrische Wahrscheinlichkeiten
• Are Most Triangles Obtuse?
  • Acht Auswahlen in sechs Sektoren
  • Drei zufällige Punkte auf einem Kreis
• Geometrische Wahrscheinlichkeit
  • In drei Teile zerbrochener Stock (trilineare Koordinaten)
  • In drei Teile zerbrochener Stock. Lösung in kartesischen Koordinaten
• Bertrand’s Paradox
• Vögel auf einem Draht (Problem und interaktive Simulation)
  • Vögel auf einem Draht: Lösung von Nathan Bowler
  • Birds on a Wire. Lösung von Mark Huber
  • Birds on a Wire: eine probabilistische Simulation. Lösung von Moshe Eliner
  • Birds on a Wire. Lösung von Stuart Anderson
  • Birds on a Wire. Lösung von Bogdan Lataianu
• Buffon’s Noodle Simulation
• Durchschnittliche Regentropfen – eine Übung in geometrischer Wahrscheinlichkeit
  • Durchschnittliche Regentropfen, Teil 2
• Rechteck auf einem Schachbrett: Eine Einführung
• Stäbchen markieren und brechen
• Zufällige Punkte auf einem Segment
• Halbkreisabdeckung
• Halbkugelabdeckung
• Überlappende Zufallsintervalle
• Zufallsintervalle mit einer Dominante
• Punkte auf einem quadratischen Gitter
• Flache Wahrscheinlichkeiten auf einer Kugel
• Wahrscheinlichkeit im Dreieck

|Kontakt||Titelseite||Inhalt||oben|

Copyright © 1996-2018 Alexander Bogomolny