Statistik-Definitionen > Friedman-Test
Was ist der Friedman-Test?
Der Friedman-Test ist ein nicht-parametrischer Test zum Auffinden von Unterschieden bei Behandlungen über mehrere Versuche hinweg. Nichtparametrisch bedeutet, dass der Test nicht davon ausgeht, dass die Daten aus einer bestimmten Verteilung (wie der Normalverteilung) stammen. Grundsätzlich wird er anstelle des ANOVA-Tests verwendet, wenn Sie die Verteilung Ihrer Daten nicht kennen.
Der Test von Friedman ist eine Erweiterung des Vorzeichentests, der bei mehreren Behandlungen verwendet wird. Wenn es nur zwei Behandlungen gibt, sind die beiden Tests identisch.
Ausführung des Tests
Ihre Daten sollten die folgenden Anforderungen erfüllen:
- Die Daten sollten ordinal (z.B. Likert-Skala) oder kontinuierlich sein,
- Die Daten stammen aus einer einzigen Gruppe, die bei mindestens drei verschiedenen Gelegenheiten gemessen wurde,
- die Stichprobe wurde mit einer Zufallsstichprobenmethode erstellt,
- die Blöcke sind voneinander unabhängig (d. h.
- Die Blöcke sind voneinander unabhängig (d. h. alle Paare sind unabhängig – eines beeinflusst das andere nicht),
- Die Beobachtungen sind innerhalb der Blöcke ohne Gleichheit geordnet.
Die Nullhypothese für den Test ist, dass die Behandlungen alle identische Auswirkungen haben oder dass sich die Stichproben in irgendeiner Weise unterscheiden. Zum Beispiel haben sie unterschiedliche Zentren, Streuungen oder Formen. Die Alternativhypothese ist, dass die Behandlungen unterschiedliche Wirkungen haben.
Bereiten Sie Ihre Daten für den Test vor.
Schritt 1: Sortieren Sie Ihre Daten in Blöcken (Spalten in einem Tabellenblatt).Für dieses Beispiel haben wir 12 Patienten, die drei verschiedene Behandlungen erhalten.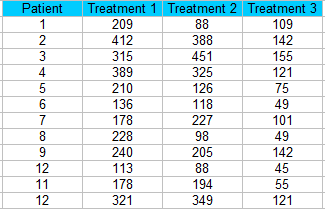
Schritt 2: Ordnen Sie jede Spalte separat. Die kleinste Punktzahl sollte den Rang 1 erhalten. Ich rangiere hier zeilenübergreifend, so dass jeder Patient für jede Behandlung eine 1, 2 oder 3 erhält.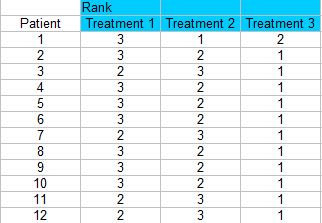
Schritt 3: Summieren Sie die Ränge (finden Sie eine Summe für jede Spalte).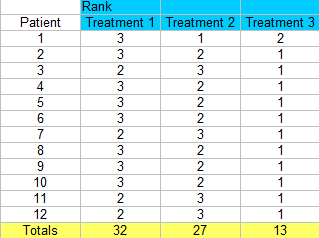
Den Test durchführen
Hinweis: Dieser Test wird normalerweise nicht von Hand durchgeführt, da die Berechnungen zeit- und arbeitsintensiv sind. Fast alle gängigen statistischen Softwarepakete können diesen Test durchführen. Ich füge jedoch die manuellen Schritte hier als Referenz ein.
Schritt 4: Berechnen Sie die Teststatistik. Sie benötigen:
- n: die Anzahl der Probanden (12)
- k: die Anzahl der Behandlungen (3)
- R: Die Gesamtzahl der Ränge für jede der drei Spalten (32, 27, 13).
Setzen Sie diese in die folgende Formel ein und lösen Sie sie: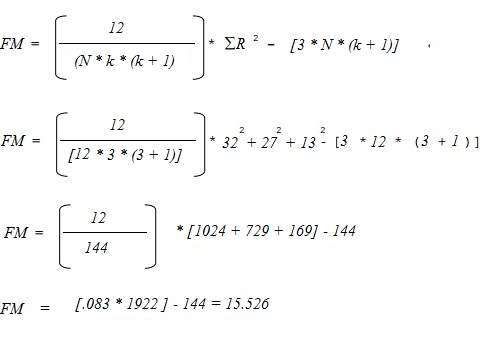
Schritt 5: Finden Sie den kritischen FM-Wert aus der Tabelle der kritischen Werte für Friedman (siehe Tabelle unten).
Verwenden Sie die Tabelle k=3 (da wir so viele Behandlungen haben) und ein Alpha-Niveau von 5%. Sie können ein höheres oder niedrigeres Alphaniveau wählen, aber 5% ist ziemlich üblich – verwenden Sie also die 5%-Tabelle, wenn Sie Ihr Alphaniveau nicht kennen.
Wenn wir n-12 in dieser Tabelle nachschlagen, finden wir einen kritischen FM-Wert von 6,17.
Schritt 6: Vergleichen Sie die berechnete FM-Teststatistik (Schritt 4) mit dem kritischen FM-Wert (Schritt 5). Verwirf die Nullhypothese, wenn der berechnete F-Wert größer ist als der kritische FM-Wert:
- Berechnete FM-Teststatistik = 15,526.
- FM-Kritischer Wert aus Tabelle = 6,17.
Die berechnete FM-Statistik ist größer, so dass Sie die Nullhypothese ablehnen würden.
Friedman’s ANOVA nach Rängen Kritischer Wert Tabelle
Drei Tabellen nach „k“.
Wenn Ihr k über 5 oder Ihr n über 13 ist, verwenden Sie die Tabelle der kritischen Werte des Chi-Quadrats in Schritt 5, um den kritischen Wert zu erhalten.
k=3
| N | α <.10 | α ≤.05 | α <.01 |
| 3 | 6.00 | 6.00 | – |
| 4 | 6.00 | 6.50 | 8.00 |
| 5 | 5.20 | 6.40 | 8.40 |
| 6 | 5.33 | 7.00 | 9.00 |
| 7 | 5.43 | 7.14 | 8.86 |
| 8 | 5.25 | 6.25 | 9.00 |
| 9 | 5.56 | 6.22 | 8.67 |
| 10 | 5.00 | 6.20 | 9.60 |
| 11 | 4.91 | 6.54 | 8.91 |
| 12 | 5.17 | 6.17 | 8.67 |
| 13 | 4.77 | 6.00 | 9.39 |
| ∞ | 4.61 | 5.99 | 9.21 |
k=4
| N | α <.10 | α ≤.05 | α <.01 |
| 2 | 6.00 | 6.00 | – |
| 3 | 6.60 | 7.40 | 8.60 |
| 4 | 6.30 | 7.80 | 9.60 |
| 5 | 6.36 | 7.80 | 9.96 |
| 6 | 6.40 | 7.60 | 10.00 |
| 7 | 6.26 | 7.80 | 10.37 |
| 8 | 6.30 | 7.50 | 10.35 |
| ∞ | 6.25 | 7.82 | 11.34 |
k=4
| N | α <.10 | α ≤.05 | α <.01 |
| 3 | 7.47 | 8.53 | 10.13 | 4 | 7.60 | 8.80 | 11.00 | 5 | 7.68 | 8.96 | 11.52 | ∞ | 7.78 | 9.49 | 13.28 |
Referenz:
Friedman’s Two-way Analysis of Variance by Ranks – Analysis of k-Within-Group Data with a
Quantitative Response Variable. Abgerufen am 17.7.2016 von: http://psych.unl.edu/psycrs/handcomp/hcfried.PDF
Stephanie Glen. „Friedman’s Test / Two Way Analysis of Variance by Ranks“ From StatisticsHowTo.com: Elementare Statistik für den Rest von uns! https://www.statisticshowto.com/friedmans-test/
——————————————————————————
Brauchen Sie Hilfe bei einer Hausaufgabe oder einer Prüfungsfrage? Mit Chegg Study können Sie Schritt-für-Schritt-Lösungen für Ihre Fragen von einem Experten auf dem Gebiet erhalten. Die ersten 30 Minuten mit einem Chegg-Lehrer sind kostenlos!