Wie viel weißt du über Unendlichkeiten? Wahrscheinlich hast du schon einmal von einer Zahl gehört, die die größtmögliche oder unmöglich große Zahl ist.

Um Unendlichkeiten zu erklären, muss ich zunächst einige Begriffe definieren.

Ganzzahlen sind Zahlen, die zum Zählen verwendet werden. Die Menge der ganzen Zahlen ist definiert als alle Zahlen ohne Bruchteile. Einige Beispiele sind: -12, 0, 1, 3, 42, 17.

Unendlichkeit ist das Konzept eines Objekts jenseits der Reichweite der natürlichen Zahlen. Es wurde erstmals von einem russischen Mathematiker namens Georg Cantor konzipiert, der nicht nur die Unendlichkeit einführte, sondern auch zeigte, dass es mehrere Unendlichkeiten gibt.

Cantor lieferte einen umstrittenen Beweis für Unendlichkeiten, der besagt, dass einige Unendlichkeiten größer sind als andere. Auf den ersten Blick mag dies unmöglich erscheinen – wie kann ein Objekt größer sein als ein anderes Objekt, das unendlich ist?

Cantor stützte seinen Beweis auf einen Zweig der Mathematik, der scheinbar nutzlos ist: Die Mengenlehre. Eine Menge ist eine Sammlung von Objekten – zum Beispiel können wir eine Menge haben, die 1, 2 und 3 enthält. Diese Objekte in der Menge werden Elemente genannt.

In mathematischer Notation würde dies wie folgt aussehen:

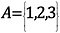
Die Anzahl der Elemente in dieser Menge, oder die Kardinalität der Menge, ist 3.

Dies wird bezeichnet als:

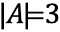
Wenn wir nun eine weitere Menge B haben, die Objekte enthält, so dass

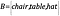
Woher wissen wir, dass die Mengen die gleiche Größe haben?

Eine Möglichkeit, dies festzustellen, besteht darin, die Anzahl der Elemente in der zweiten Menge zu zählen. Wir können deutlich sehen, dass diese Menge auch 3 Elemente hat, und so wissen wir, dass sie die gleiche Größe haben.

Eine andere Möglichkeit, dies zu tun, ist, unsere zweite Menge, B, mit unserer ersten Menge, A, zu vergleichen, indem wir sie abbilden.

Wir können das erste Element von Menge A, 1, dem ersten Element von Menge B, Stuhl, zuordnen.

Das zweite Element aus der Menge A, 2, können wir auf das zweite Element der Menge B, Tisch, abbilden.

Das dritte Element aus der Menge A, 3, können wir auf das dritte Element der Menge B, Hut, abbilden.

Da jedes Element aus A auf genau ein Element aus B abgebildet wird, sind die Mengen gleich groß.

Werfen wir nun einen Blick auf unendliche Mengen. Die Menge der ganzen Zahlen, die eingangs erwähnt wurde, ist eine unendliche Menge – es gibt unendlich viele ganze Zahlen. Die Menge der ganzen Zahlen wird mit dem Symbol

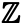
die Menge der geraden Zahlen bezeichnet, die wir als

bezeichnen können, ist definiert als

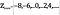
Intuitiv, kann es so aussehen

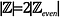
weil es für jede gerade ganze Zahl 2 ganze Zahlen gibt: 1 ungerade ganze Zahl und 1 gerade ganze Zahl. Überprüfen wir das.

Versuchen wir, die Mengen zu vergleichen, indem wir Elemente von einer Menge auf die andere abbilden.

Wir können 1 auf 2 abbilden, 2 auf 4, 3 auf 6, und so weiter.

Wenn wir dies für alle Mengen tun, können wir sehen, dass jedes Element aus der ganzzahligen Menge auf genau 1 Element aus der geraden ganzzahligen Menge abgebildet wird.

Auch wenn es kontraintuitiv erscheinen mag, ist die Größe der Mengen gleich.