Das Ising-Modell ist ein besonderes Beispiel für ein thermodynamisches System, und es ist das Modellsystem zum Verständnis von Phasenübergängen. Wissen Sie, wie viele Biologen so viel Zeit mit mickrigen Fruchtfliegen verbringen? Nun, Physiker verbringen sehr viel Zeit mit dem Ising-Modell. Wie uns Prof. Raghu hilfreich mitteilt, ist es die Drosophila der Phasenübergänge.

Persönlich bin ich nicht der größte Fan seiner Analogie, weil ich Fruchtfliegen eklig finde. Hoffentlich ist das Ising-Modell nicht zu eklig.

Motivation

Warum sollten wir so viel Zeit damit verbringen, über das Ising-Modell zu sprechen?

• Es ist überraschend nützlich, um uns dabei zu helfen, über alle Arten von Verhaltensweisen im Zusammenhang mit Phasenübergängen nachzudenken. Zum Beispiel:

  • das Ising-Modell zeigt Symmetriebrechungen in der Tieftemperaturphase (über die wir gerade gesprochen haben)

  • es hat einen speziellen „kritischen Punkt“ bei einer genau definierten Temperatur (auf den wir im Phasendiagramm von Wasser angespielt haben)

  • andere interessante Eigenschaften.

• Es ist eines der wenigen exakt lösbaren Modelle, bei denen wir tatsächlich thermodynamische Größen berechnen und interpretieren können.

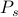  • Im Allgemeinen ist die Berechnung thermodynamischer Größen schwierig, weil man viele Terme zusammenzählen muss. Erinnere dich an unseren ersten Thermokurs, dass man sich ein Gleichgewichtssystem als ein Ensemble vieler Zustände vorstellen kann, von denen jeder mit seiner eigenen Wahrscheinlichkeit gewichtet ist. In diesem Rahmen entsprechen die beobachteten thermodynamischen Größen den Durchschnittswerten des Ensembles. Wenn man den Ensemble-Durchschnitt einer Beobachtungsgröße 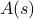finden will, muss man die Summe 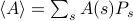finden, wobei die Summe über alle möglichen Zustände läuft. Das Problem dabei ist, wie Sie sich erinnern, dass die Anzahl der Zustände eines thermodynamischen Systems exponentiell mit der Anzahl der Teilchen skaliert! Selbst für ein mittelgroßes System gibt es einfach zu viele Zustände, als dass ein Computer den Durchschnitt explizit berechnen könnte – ganz zu schweigen von einem thermodynamischen System, bei dem 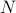in der Größenordnung von 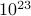liegt.

  • Wir müssen also “schlau sein“, um die Verteilungsfunktion zu berechnen, und wir sollten für exakt lösbare Systeme dankbar sein!

• Das Ising-Modell ist einfach, kann aber auf eine erstaunliche Anzahl verschiedener Systeme angewandt werden.

  • Das ist unser erster Vorgeschmack auf die Universalität – ein Merkmal kritischer Phänomene, bei denen dieselbe Theorie auf alle möglichen verschiedenen Phasenübergänge anwendbar ist, sei es in Flüssigkeiten und Gasen oder Magneten oder Supraleitern oder was auch immer. Physiker lieben diese Art von allgemeinem Verhalten, weil es auf eine Art tiefere Ordnung in unserer chaotischen Welt hindeutet.

Definition des Ising-Modells

Das Ising-Modell ist ein mathematisches Modell, das nicht einem tatsächlichen physikalischen System entspricht. Es ist ein riesiges (quadratisches) Gitter von Stellen, wobei jede Stelle einen von zwei Zuständen annehmen kann. Wir kennzeichnen jede Seite mit einem Index und nennen die beiden Zustände und . Um zu sagen, dass sich die -te Stelle im Zustand befindet, schreiben wir .

Nun ist diese Definition erbärmlich abstrakt und unphysikalisch, so dass es für uns Physiker äußerst hilfreich ist, ein tatsächliches System vor Augen zu haben, so dass wir uns auf etwas Explizites beziehen und eine physikalische Intuition aufbauen können. Hier sind ein paar physikalische Systeme, die das Ising-Modell darstellen könnte:

• Ein Magnet. Jede Seite repräsentiert einen bestimmten „Spin“ im Material (ein ungepaartes Elektron??) und ist , wenn der Spin nach unten zeigt, oder , wenn der Spin nach oben zeigt. Jeder der Spins verhält sich wie ein Mini-Magnet mit seinem eigenen Mini-Magnetmoment; wenn alle Spins ausgerichtet sind, verhält sich das gesamte Gitter der Spins wie ein großer Magnet mit einem makroskopischen Netto-Magnetmoment.

• Eine Legierung, zum Beispiel Messing. Jede der Stellen ist ein Atom im Gitter; steht für ein Kupferatom an dieser Stelle; steht für Zink.

• Ein “Gittergas“. Jede der Stellen ist der mögliche Standort eines Teilchens; bedeutet, dass die Stelle leer ist, und bedeutet, dass die Stelle von einem Teilchen besetzt ist.

• Bakterielle Wirbelgitter???

Fürs Erste betrachten wir das Ising-Modell als ein Modell für einen Magneten. Es handelt sich dabei um ein stark vereinfachtes Spielzeugmodell eines Magneten, aber die Magnetanalogie kann uns dennoch dabei helfen, unsere geschätzte physikalische Intuition zu lenken.

Zusammenstellung der Hamiltonfunktion

Eine natürliche Frage, die man sich bei diesem Micky-Maus-Modell eines Magneten stellen kann, ist, welche Energie es hat. Um genauer zu sein, wollen wir eine Funktion aufschreiben, die die Energie jeder einzelnen möglichen Konfiguration (auch Mikrozustand genannt) der Spins im Magneten darstellt. Wie wir wissen, wird diese Energiefunktion Hamiltonian genannt.

Im Ising-Modell enthält der Hamiltonian zwei Arten von Wechselwirkungen:

• den externen Feldterm. Wie wir uns aus der Quantenmechanik erinnern, kann ein äußeres Magnetfeld die Energien des Spin-down- und des Spin-up-Zustands aufspalten, so dass der eine Zustand eine höhere Energie hat und der andere eine niedrigere.

  • Die Größe von stellt dar, wie stark das Feld ist, und gibt an, wie viel höher die Energie des einen Spins ist als die des anderen.

  • Das Vorzeichen von gibt an, ob der Spin-up oder der Spin-down bevorzugt wird.

  • Da jeder einzelne Spin das äußere Feld spürt, müssen wir über alle Stellen summieren, um den Gesamtbeitrag zur Energie zu finden.

• Der Wechselwirkungsterm zwischen benachbarten Spins – vielleicht wollen sie sich zueinander ausrichten und in dieselbe Richtung zeigen, vielleicht wollen sie sich gegeneinander ausrichten und in unterschiedliche Richtungen zeigen. Physikalisch gesehen können wir uns vorstellen, dass diese Wechselwirkung entsteht, weil jeder Spin im Magneten ein eigener kleiner magnetischer Dipol ist, der sein eigenes Magnetfeld aufbaut, und seine Nachbarn dieses Magnetfeld spüren können.

  • Die Größe von gibt an, wie stark benachbarte Spins aneinander gekoppelt sind – wie sehr sie sich (anti-)ausrichten wollen. Physikalisch gesehen könnte die Stärke der Spin-Spin-Kopplung z.B. vom Abstand zwischen den Spins im Magentgitter abhängen.

  • Das Vorzeichen von gibt an, ob sich die Nachbarn eher ausrichten oder nicht ausrichten. (Der Fachausdruck dafür ist ferromagnetisch bzw. antiferromagnetisch). Ob ein Material das eine oder das andere (oder keines von beiden) ist, hängt von den genauen quantenmechanischen Details der Wechselwirkung zwischen den Spins ab.

  • Da die Spin-Spin-Wechselwirkung zwischen zwei Spins auftritt, müssen wir über die Paare von Stellen summieren, um die gesamte Wechselwirkung zur Energie zu finden.

Mehr über den Wechselwirkungsterm

Eine natürliche Frage über den Spin-Spin-Wechselwirkungsterm ist, welche Spins mit welchen Spins gekoppelt sind?

Wenn wir uns wieder dem physikalischen Bild des Magneten zuwenden und auf einen bestimmten Spin zoomen, würden wir erwarten, dass die Stärke der Spin-Spin-Wechselwirkung für nahe Spins stärker und für weit entfernte Spins schwächer ist. Die genaue Entfernungsabhängigkeit der Spin-Spin-Wechselwirkung ist bei realen Magneten wahrscheinlich ziemlich kompliziert.

Für das Ising-Modell nehmen wir die einfachste mögliche Annahme für die Art dieser Spin-Spin-Wechselwirkung an:

Ein paar Anmerkungen:

• In einem quadratischen Gitter mit Dimensionen hat jede Stelle 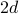nächste Nachbarn: links und rechts in einer Dimension, oben und unten, sobald man die zweite Dimension hinzufügt, usw…

• Wir nehmen an, dass die Wechselwirkung isotrop ist – alle Nachbarn werden unabhängig von der Richtung gleich behandelt.

• Wir sprechen oft über Wechselwirkungen zwischen nächsten Nachbarn als die Energie einer Bindung, die zwei Gitterplätze miteinander verbindet.

• Wenn wir über benachbarte Paare von Stellen summieren, schreiben wir symbolisch kleine spitze Klammern um die Indizes, um „nächster Nachbar“ zu repräsentieren.

Eine nette Konsequenz der Wechselwirkungen zwischen nächsten Nachbarn ist, dass wir, wenn wir die Gesamtenergie einer bestimmten Konfiguration von Spins finden, nicht über alle möglichen Paare von Stellen summieren, sondern nur über Paare von Stellen, die einander benachbart sind.

Nachdem wir nun all diese Dinge besprochen haben, sind wir bereit, den eigentlichen Ausdruck für den Hamiltonian aufzuschreiben. (Ich wollte die Physik erklären und interpretieren, bevor ich den Hamiltonian aufschreibe, damit die Symbole einen Sinn ergeben.)

Hamiltonian des Ising-Modells

Der Hamiltonian des Ising-Modells kann geschrieben werden als

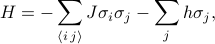
wobei die Spin-Spin-Wechselwirkung darstellt, das äußere Feld repräsentiert und die 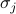die einzelnen Spins auf jedem der Gitterplätze sind. Die erste Summe bezieht sich auf alle Paare benachbarter Gitterplätze (auch bekannt als Bindungen); sie stellt die Wechselwirkungen zwischen den Spins dar. Die zweite Summe bezieht sich auf alle Gitterplätze selbst; sie stellt das externe Feld dar, das versucht, alle Spins in eine Richtung auszurichten.

Weiter zur Thermodynamik des Ising-Modells.