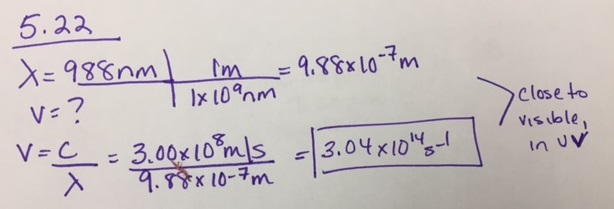Elektromagnetische Strahlung
Energie, die in Form von periodischen Schwingungen elektrischer und magnetischer Felder durch den Raum übertragen bzw. abgestrahlt wird, bezeichnet man als elektromagnetische Strahlung. (Abbildung \(\PageIndex{2}\)). Einige Formen der elektromagnetischen Strahlung sind in Abbildung \(\PageIndex{4}\)) dargestellt. In einem Vakuum bewegen sich alle Formen elektromagnetischer Strahlung – ob Mikrowellen, sichtbares Licht oder Gammastrahlen – mit Lichtgeschwindigkeit (c), einer physikalischen Grundkonstante mit einem Wert von 2,99792458 × 108 m/s (das sind etwa 3,00 ×108 m/s oder 1,86 × 105 mi/s). Dies ist etwa eine Million Mal schneller als die Schallgeschwindigkeit.
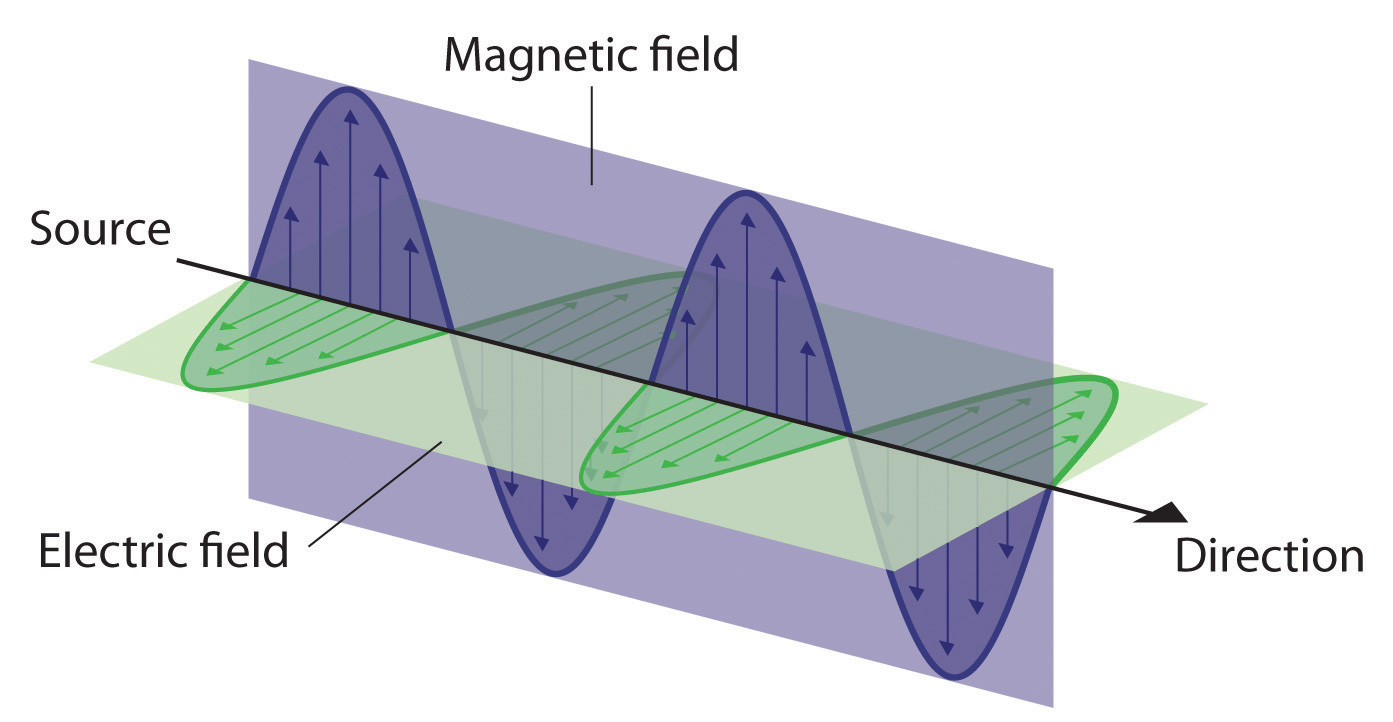
Da die verschiedenen Arten der elektromagnetischen Strahlung alle die gleiche Geschwindigkeit (c) haben, unterscheiden sie sich nur in Wellenlänge und Frequenz. Wie in Abbildung \(\PageIndex{3}\) und Tabelle \(\PageIndex{1}\) dargestellt, reichen die Wellenlängen der bekannten elektromagnetischen Strahlung von 101 m für Radiowellen bis zu 10-12 m für Gammastrahlen, die von Kernreaktionen ausgesendet werden. Die nachstehende Gleichung zeigt, dass die Frequenz der elektromagnetischen Strahlung umgekehrt proportional zu ihrer Wellenlänge ist:
\
Die Frequenz der Radiowellen beträgt beispielsweise etwa 108 Hz, während die Frequenz der Gammastrahlen etwa 1020 Hz beträgt. Sichtbares Licht, also elektromagnetische Strahlung, die vom menschlichen Auge wahrgenommen werden kann, hat Wellenlängen zwischen etwa 7 × 10-7 m (700 nm oder 4,3 × 1014 Hz) und 4 × 10-7 m (400 nm oder 7,5 × 1014 Hz). Es ist zu beachten, dass mit steigender Frequenz die Wellenlänge abnimmt; c ist eine Konstante und bleibt gleich. Ähnlich verhält es sich, wenn die Frequenz abnimmt, nimmt die Wellenlänge zu.
Gleichung 5.2.1 und die Lichtgeschwindigkeit (mit Einheiten) einprägen. Außerdem ist es wichtig zu wissen, welche Seite des elektromagnetischen Spektrums tödlich ist.
| Einheit | Symbol | Wellenlänge (m) | Art der Strahlung |
|---|---|---|---|
| Pikometer | pm | 10-12 | Gamma-Strahl |
| Nanometer | nm | 10-9 | x-ray |
| micrometer | μm | 10-6 | infrared |
| millimeter | mm | 10-3 | infrared |
| Zentimeter | cm | 10-2 | Mikrowelle |
| Meter | m | 100 | Funk |
Licht verhält sich ebenfalls wie ein Energiepaket. Es stellt sich heraus, dass bei Licht die Energie des „Energiepakets“ proportional zu seiner Frequenz ist.
\
\
Während sichtbares Licht für unsere Haut im Wesentlichen harmlos ist, hat ultraviolettes Licht mit Wellenlängen von ≤ 400 nm genug Energie, um unsere Haut in Form von Sonnenbrand schwer zu schädigen. Da die Ozonschicht Sonnenlicht mit einer Wellenlänge von weniger als 350 nm absorbiert, schützt sie uns vor den schädlichen Auswirkungen der hochenergetischen ultravioletten Strahlung.
In diesem Kurs werden wir keine Energieberechnungen durchführen. Du solltest die Beziehung zwischen Frequenz und Energie kennen. Sie werden auch erkennen, dass kurzwellige Strahlung mit einer hohen Energie verbunden ist.
Die Energie elektromagnetischer Strahlung steigt mit zunehmender Frequenz und abnehmender Wellenlänge.
Beispiel \(\PageIndex{1}\)
Wie hoch ist die Frequenz des Lichts, wenn seine Wellenlänge 5,55 × 10-7 m beträgt?
Lösung
Wir verwenden die Gleichung, die die Wellenlänge und die Frequenz des Lichts mit seiner Geschwindigkeit in Beziehung setzt. Wir haben
\
Wir teilen beide Seiten der Gleichung durch 5,55 × 10-7 m und erhalten
\
Beachte, wie sich die Einheiten m aufheben und s im Nenner übrig bleibt. Eine Einheit im Nenner wird durch eine -1-Potenz – s-1 – angezeigt und als „pro Sekunde“ gelesen.
Übung \(\PageIndex{1}\)
Wie groß ist die Wellenlänge (in mm) des Lichts, wenn seine Frequenz 1 ist.55 × 1010 s-1?
Antwort
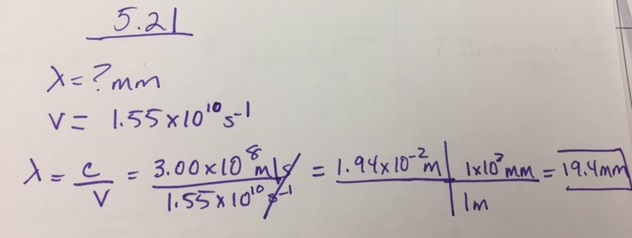
Beispiel \(\PageIndex{2}\)
Berechnen Sie die Frequenz einer Strahlung, wenn ihre Wellenlänge 988 nm beträgt. Wo erscheint diese Strahlung im elektromagnetischen Spektrum?
Antwort