Variansen er et tal, der angiver, hvor langt et sæt tal ligger fra hinanden.Variansen er identisk med den kvadrerede standardafvigelse og udtrykker derfor “det samme” (men i højere grad).
Varians – Eksempel
En undersøgelse lader 100 personer udføre en simpel hastighedsopgave i løbet af 80 forsøg. For hver deltager registreres der således 80 reaktionstider (i sekunder). En del af disse data er vist nedenfor.

I undersøgelser som disse ser vi typisk, at folk bliver hurtigere, efterhånden som de udfører hastighedsopgaven oftere. Det vil sige, at den gennemsnitlige reaktionstid har tendens til at falde i løbet af forsøg.
Også vil reaktionstiderne typisk variere mindre mellem forskellige personer i det omfang, de udfører opgaven oftere. Teknisk set siger vi, at variansen aftager over forsøg. Nedenstående tabel illustrerer dette for forsøg 1,4,7 og 10.
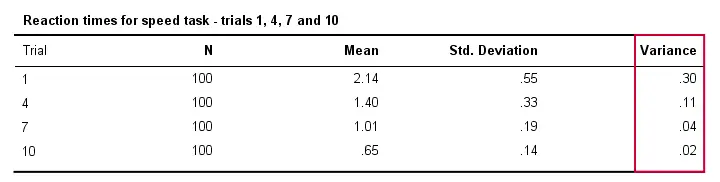
Varians og histogram
En god måde at visualisere dataene fra vores tidligere tabel på er et histogram for hvert forsøg. På den måde illustrerer figuren nedenfor, at deltagerne blev hurtigere over forsøg; fra forsøg 1 til forsøg 10 bevæger histogramstængerne sig mod venstre, mod 0 sekunder.
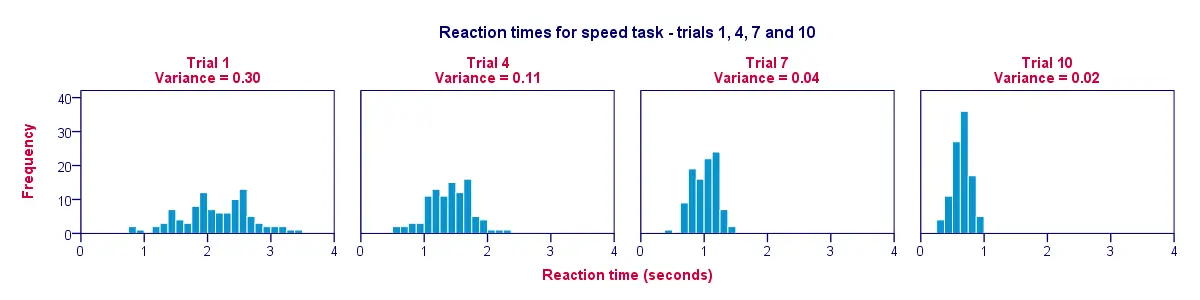
Et andet resultat er, at histogrammerne bliver smallere (og dermed højere), når vi bevæger os fra forsøg 1 til forsøg 10; dette illustrerer, at reaktionstiderne varierer mindre og mindre mellem vores deltagere, efterhånden som forsøget skrider frem. Variansen falder over forsøgene.
Varians – populationsformel
En grundlæggende formel til beregning af variansen er
$$$$S^2 = \frac{\sum(X – \overline{X})^2}{n}$$$
Vi anbefaler, at du prøver at forstå, hvad denne formel gør, da det hjælper meget på forståelsen af ANOVA (= variansanalyse). Vi vil derfor demonstrere den på blot en håndfuld data.
Varians – GoogleSheets
For enkelhedens skyld vil vi skære vores data ned til det første forsøg for de første 5 deltagere. Disse 5 reaktionstider -og en manuel beregning af deres varians- findes i dette GoogleSheet.
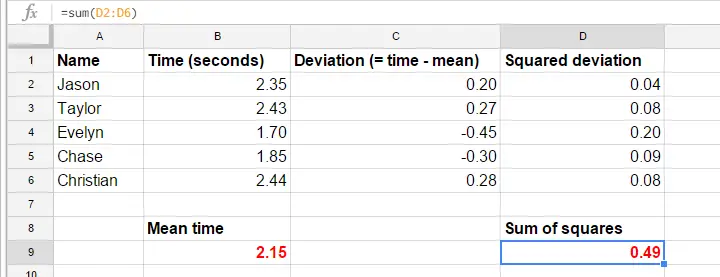
Varians – Beregningsskridt
Formlerne i GoogleSheet viser præcist, hvordan man beregner en varians. De grundlæggende trin er
- beregn den gennemsnitlige reaktionstid (2,15);
- beregn afvigelsespoint (reaktionstid minus den gennemsnitlige reaktionstid);
- beregn kvadrerede afvigelsespoint;
- tilføj kvadrerede afvigelsespoint. Resultatet (0,49) er en sum af kvadrater, den vigtigste byggesten i ANOVA;
- divider summen af kvadrater med antallet af observationer (5 reaktionstider).
Alternativt kan du beregne en varians ved at indtaste =VARP(B2:B6) i en celle (B2:B6 er de celler, der indeholder vores 5 reaktionstider). VARP er en forkortelse for “varianspopulation”. OpenOffice og MS Excel indeholder lignende formler.
Varians – prøveformel
Som for standardafvigelsen vil ovennævnte formel systematisk undervurdere variansen i populationen, hvis vores data er en simpel tilfældig prøve fra en meget større population, hvis vores data er en simpel tilfældig prøve fra en meget større population. I dette tilfælde vil vi bruge en lidt anden formel:
$$$$S^2 = \frac{\sum(X_i – \overline{X})^2}{n – 1}$$$
Hvilken formel vi skal bruge afhænger således af vores data: indeholder de hele den population, som vi gerne vil undersøge, eller er de blot en stikprøve fra denne population?
Da vores 100 deltagere tydeligvis er en stikprøve, vil vi bruge stikprøveformlen. I GoogleSheets giver indtastning af =VAR(B2:B6) i en eller anden celle stikprøvevariansen.
Varians i SPSS
Så vidt vi ved, er formlen for populationsvariansen helt fraværende i SPSS, og det betragter vi som en alvorlig mangel. I stedet bruger SPSS altid stikprøveformlen. dette gælder både for variansen mellem forsøgspersoner (som behandles i denne vejledning) og for variansen inden for forsøgspersoner. Relevant output er vist nedenfor.

Med hensyn til denne outputtabel skal du også bemærke, at variansen faktisk er den kvadrerede standardafvigelse (bortset fra afrunding).
Med hensyn til variansen, er det sådan set det hele. Vi håber, at du fandt denne vejledning nyttig til at forstå, hvad en varians er.