Uønsket konvolution er et iboende problem i forbindelse med overførsel af analog information. F.eks. kan alt følgende modelleres som en konvolution: billedforvrængning i et rystet kamera, ekko i langdistancetelefonopkald, den uendelige båndbredde i analoge sensorer og elektronik osv. Dekonvolution er processen med at filtrere et signal for at kompensere for en uønsket konvolution. Målet med dekonvolution er at genskabe signalet, som det var, før konvolutionen fandt sted. Dette kræver normalt, at egenskaberne ved konvolutionen (dvs. impuls- eller frekvensresponsen) er kendt. Dette kan skelnes fra blind dekonvolution, hvor egenskaberne ved den parasitære konvolution ikke er kendt. Blind dekonvolution er et langt vanskeligere problem, som ikke har nogen generel løsning, og fremgangsmåden skal skræddersys til den særlige anvendelse.

Dekonvolution er næsten umulig at forstå i tidsdomænet, men er ret ligetil i frekvensdomænet. Hver sinusoid, som det oprindelige signal består af, kan ændres i amplitude og/eller fase, når den passerer gennem den uønskede konvolution. For at udtrække det oprindelige signal skal dekonvolutionsfilteret ophæve disse amplitude- og faseændringer. Hvis f.eks.

f.eks. konvolutionen ændrer en sinusoidens amplitude med 0,5 med en faseforskydning på 30 grader, skal dekonvolutionsfilteret forstærke sinusoidens amplitude med 2,0 med en faseændring på -30 grader.

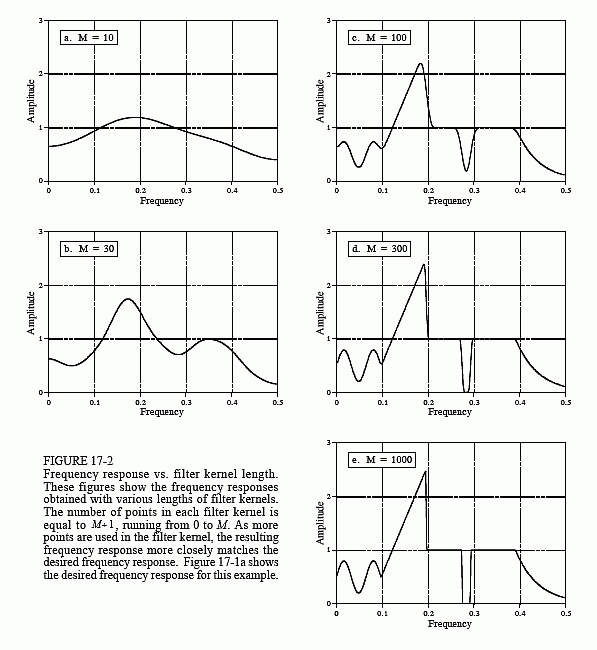
Det eksempel, vi vil bruge til at illustrere dekonvolutionen, er en gammastråledetektor. Som illustreret i fig. 17-3 består denne anordning af to dele, en scintillatorog en lysdetektor. En scintillator er en særlig type gennemsigtigt materiale, f.eks. natriumjodid eller bismuth germanat. Disse forbindelser omdanner energien i hver gammastråle til et kort udbrud af synligt lys. Dette lys

omdannes derefter til et elektronisk signal af en lysdetektor, f.eks. en fotodiode eller et fotomultiplikatorrør. Hver impuls, der produceres af detektoren, ligner en ensidig eksponentiel, med en vis afrunding af hjørnerne. Denne form bestemmes af egenskaberne ved den anvendte scintillator. Når en gammastråle afgiver sin energi til scintillatoren, bliver de nærliggende atomer exciteret til et højere energiniveau. Disse atomer deexciteres tilfældigt og producerer hver en enkelt foton synligt lys. Nettoresultatet er en lyspuls, hvis amplitude aftager i løbet af nogle få hundrede nanosekunder (for natriumjodid). Da ankomsten af hver gammastråle er en impuls, er udgangspulsen fra detektoren (dvs. den ensidige eksponentiel) systemets impulssvar.

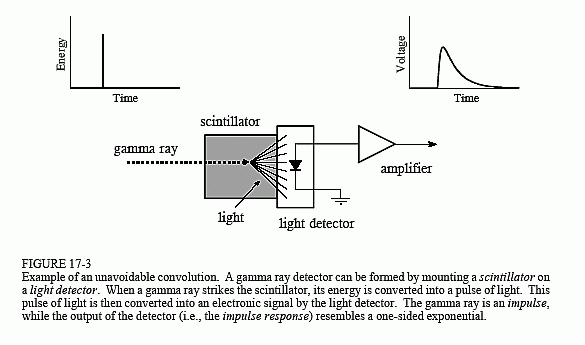
Figur 17-4a viser de impulser, der genereres af detektoren som reaktion på tilfældigt ankommende gammastråler. Den information, som vi gerne vil uddrage af dette udgangssignal, er amplituden af hver enkelt impuls, som er proportional med energien af den gammastråle, der genererede den. Det er en nyttig information, fordi energien kan fortælle interessante ting om, hvor gammastrålen har været. Det kan f.eks. give medicinske oplysninger om en patient, fortælle alderen af en fjern galakse, afsløre en bombe i flybagage osv.

Alt ville være fint, hvis der kun lejlighedsvis blev opdaget en gammastråle, men det er normalt ikke tilfældet. Som vist i (a) kan to eller flere impulser overlappe hinanden,hvilket forskyder den målte amplitude. En løsning på dette problem er at dekonvolvere detektorens udgangssignal og gøre impulserne smallere, således at der sker mindre overlapning. Ideelt set vil vi gerne have, at hver enkelt impuls ligner den oprindelige impuls. Som du måske kan ane, er dette ikke muligt, og vi må nøjes med en impuls, der er endelig i længde, men betydeligt kortere end den detekterede impuls. Dette mål er illustreret i fig. 17-4b.

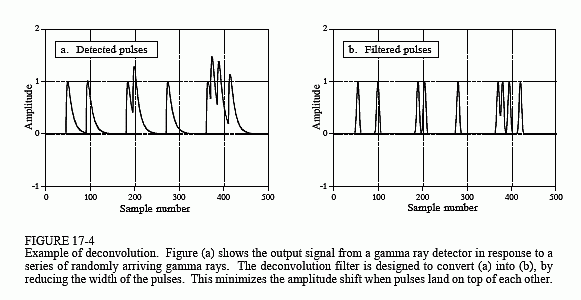
Selv om detektorsignalet har sin information kodet i tidsdomænet, må en stor del af vores analyse foretages i frekvensdomænet, hvor problemet er lettere at forstå. Figur 17-5a er det signal, der produceres af detektoren(noget, vi kender). Figur (c) er det signal, som vi ønsker at få (også noget, vi ved). Denne ønskede puls blev vilkårligt valgt til at have samme form som et Blackman-vindue med en længde på ca. en tredjedel af den oprindelige puls. Vores mål er at finde en filterkerne (e), som ved konvolvering med signalet i (a) giver signalet i (c). I ligningsform: hvis a * e = c, og givet a og c, find.

Hvis disse signaler blev kombineret ved addition eller multiplikation i stedet for konvolution, ville løsningen være let: subtraktion bruges til at “de-addere”, og division bruges til at “de-multiplikere”. Konvolution er anderledes; der findes ikke en simpel omvendt operation, som kan kaldes “dekonvolution”. Konvolution er for rodet til at kunne ophæves ved direkte at manipulere tidsdomænesignalerne.

Det er heldigvis nemmere at løse dette problem i frekvensdomænet. Husk, at konvolution i det ene domæne svarer til multiplikation i det andet domæne. Igen med henvisning til signalerne i fig. 17-5: hvis b × f = d, og givet b og d, find f. Dette er et let problem at løse: filterets frekvensrespons, (f), er frekvensspektret af den ønskede puls, (d), divideret med frekvensspektret af den registrerede puls, (b). Da den detekterede puls er asymmetrisk, vil den have en fase, der ikke er nul. Det betyder, at der skal anvendes en kompleks division (dvs. en fase af størrelsen & divideret med en anden fase af størrelsen &). Hvis du skulle have glemt det, er det i kapitel 9 defineret, hvordan man udfører en kompleks division af et spektrum med et andet. Den nødvendige filterkerne, (e), findes derefter ud fra frekvensresponsen ved hjælp af den brugerdefinerede filtermetode (IDFT, shift, truncate, &multiplikere med et vindue).

Der er grænser for den forbedring, som dekonvolution kan give. Med andre ord, hvis du bliver grådig, vil tingene falde fra hinanden. At blive grådig i dette eksempel betyder, at man forsøger at gøre den ønskede puls overdrevent smal. Lad os se på, hvad der sker. Hvis den ønskede puls gøres smallere, må dens frekvensspektrum indeholde flere højfrekvente komponenter. Da disse højfrekvente komponenter har en meget lav amplitude i den registrerede puls, skal filteret have en meget høj forstærkning ved disse frekvenser. F.eks. viser (f), at nogle frekvenser skal multipliceres med en faktor tre for at opnå den ønskede puls (c). Hvis den ønskede puls gøres smallere, vil forstærkningen af dekonvolutionsfilteret være endnu større ved høje frekvenser.

Problemet er, at små fejl er meget uforsvarlige i denne situation. Hvis f.eks. en frekvens forstærkes med 30, når der kun er behov for 28, vil det dekonvolutionerede signal sandsynligvis blive et rod. Når dekonvolutionen presses til større præstationsniveauer, skal egenskaberne ved den uønskede konvolution forstås med større nøjagtighed og præcision. Der er altid ubekendte faktorer i virkelige anvendelser i den virkelige verden, som skyldes f.eks. elektronisk støj, temperaturdrift, variationer mellem enheder osv. Disse ubekendte faktorer sætter en grænse for, hvor godt dekonvolutionen vil fungere.

Selv om den uønskede konvolution er perfekt forstået, er der stadig et forhold, der begrænser dekonvolutionens ydeevne: støj. De fleste uønskede konvolutioner har f.eks. form af et lavpasfilter, der reducerer amplituden af de højfrekvente komponenter i signalet. Dekonvolution korrigerer dette ved at forstærke disse frekvenser. Hvis amplituden af disse komponenter imidlertid falder under systemets iboende støj, går den information, der er indeholdt i disse frekvenser, tabt. Ingen signalbehandling kan hente den tilbage. Den er væk for altid. Adios! Farvel! Sayonara! Forsøg på at genvinde disse data vil kun forstærke støjen. I ekstreme tilfælde kan amplituden af nogle frekvenser blive helt reduceret til nul. Dette vil ikke blot udslette oplysningerne, men også forsøge at få dekonvolutionsfilteret til at have uendelig forstærkning ved disse frekvenser. Løsningen er at konstruere et mindre aggressivt dekonvolutionsfilter og/eller at sætte grænser for, hvor meget forstærkning der er tilladt ved nogen af frekvenserne.

Hvor langt kan man gå? Hvor grådigt er for grådigt? Det afhænger helt og holdent af det problem, som man forsøger at løse. Hvis signalet er velopført og har lavt støjniveau, kan der sandsynligvis foretages en betydelig forbedring (tænk på en faktor 5-10). Hvis signalet ændrer sig over tid, ikke er særlig godt forstået eller er støjende, vil du ikke opnå nær så gode resultater (tænk på en faktor 1-2). En vellykket dekonvolution kræver en hel del afprøvning. Hvis det virker på et vist niveau, så prøv at gå længere; du vil vide, når det falder fra hinanden. Intet teoretisk arbejde vil give dig mulighed for at omgå denneiterative proces.

Dekonvolution kan også anvendes på signaler, der er kodet i frekvensdomænet. Et klassisk eksempel er restaureringen af gamle optagelser af den berømte operasanger Enrico Caruso (1873-1921). Disse optagelser blev foretaget med et efter moderne standarder meget primitivt udstyr. Det største problem er resonanserne i det lange rørformede optagehorn, der blev brugt til at opsamle lyden. Når sangeren tilfældigvis rammer en af disse resonansfrekvenser, stiger lydstyrken i optagelsen brat. Digital dekonvolution har forbedret den subjektive kvalitet af disse optagelser ved at

reducere de høje pletter i musikken. Vi vil kun beskrive den generelle metode; for en detaljeret beskrivelse henvises til den originale artikel: T. Stockham, T. Cannon ogR. Ingebretsen, “Blind Deconvolution Through Digital Signal Processing”,Proc. IEEE, vol. 63, Apr. 1975, pp. 678-692.

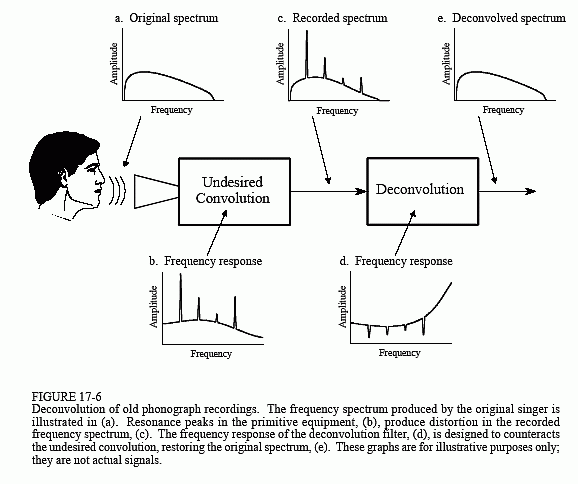
Figur 17-6 viser den generelle fremgangsmåde. Frekvensspektret af det oprindelige lydsignal er illustreret i (a). Figur (b) viser kontrolapparatets frekvensrespons, en relativt jævn kurve bortset fra flere skarpe resonanstoppe. Spektret af det optagede signal, vist i (c), er lig med det sande spektrum, (a), ganget med den ujævne frekvensrespons, (b). Målet med dekonvolutionen er at modvirke den uønskede konvolution. Med andre ord skal frekvensresponsen for dekonvolutionsfilteret,(d), være det omvendte af (b). Det vil sige, at hver top i (b) ophæves af et tilsvarende fald i (d). Hvis dette filter var perfekt udformet, ville det resulterende signal have et spektrum, (e), der var identisk med det originale.

Her er problemet: det originale optageudstyr er for længst blevet kasseret, og dets frekvensrespons, (b), er et mysterium. Med andre ord er der tale om et problem med blinddekonvolution; hvis vi kun har (c), hvordan kan vi så bestemme (d)?

Blinde dekonvolutionsproblemer angribes normalt ved at foretage et skøn eller en formodning om de ukendte parametre. For at behandle dette eksempel antages det gennemsnitlige spektrum af den originale musik at svare til det gennemsnitlige spektrum af den samme musik udført af en nutidig sanger ved hjælp af moderne udstyr. Gennemsnitsspektret findes ved hjælp af teknikkerne i kapitel 9: signalet opdeles i et stort antal segmenter, DFT’en for hvert segment tages, konverteres til polær form og derpå beregnes gennemsnittet af størrelserne sammen. I det enkleste tilfælde er den ukendte frekvensgang lig med det gennemsnitlige spektrum af den gamle optagelse divideret med det gennemsnitlige spektrum af den moderne optagelse. (Den metode, der anvendes af Stockham et al., er baseret på en mere sofistikeret teknik kaldet homomorphic processing, som giver et bedre skøn over optagelsessystemets karakteristika).