Sådan beregner man spændingen i reb, der hænger en genstand op

Vi kan se i illustrationen nedenfor, at den kraft, F, der er nødvendig for at løfte genstanden, er lig med genstandens vægt, W. Denne idé er det grundlæggende begreb, der ligger til grund for vores spændingskraftformel. Nedenfor er også vist objektets frikropsdiagram, som viser de spændingskræfter, T, der virker i snoren. Som du kan se, kommer spændingskræfterne parvis og i modsatte retninger:

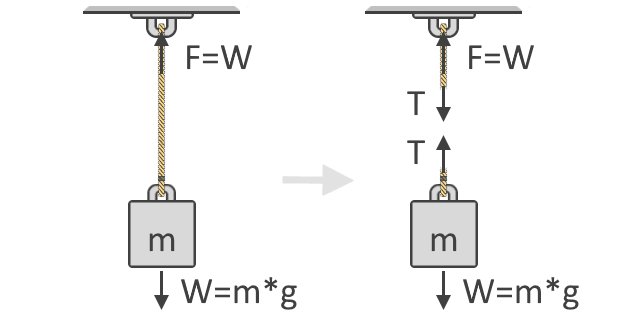
I overensstemmelse med Newtons anden bevægelseslov kan vi så udtrykke summen af kræfter ved hjælp af genstandens fritekropsdiagram, som vist i højre side af illustrationen ovenfor. Vi bruger fritekropsdiagrammer til at vise de forskellige retninger og størrelser af de kræfter, der virker på et legeme. I ligevægt skal disse kræfter alle være lig med nul. Hvis man betragter alle opadrettede kræfter som positive og nedadrettede som negative, er vores ligning:

ΣF = 0 = T + (-W)
T = W
hvor vægten, W, bliver negativ, da den er rettet nedad. Ved at overføre W til den anden side af ligningen kan vi nu se, at spændingskraften i rebet er lig med vægten af den genstand, det bærer, som også vist ovenfor.

Hvis vi bruger flere reb til at løfte genstanden, bliver den samlede spændingskraft delt op på rebene. Spændingskraften i hvert reb afhænger af deres vinkler i forhold til retningen af den kraft, som det modvirker. For yderligere at forstå dette, lad os betragte et andet fritekropsdiagram af en genstand ophængt i to reb, som vist nedenfor:

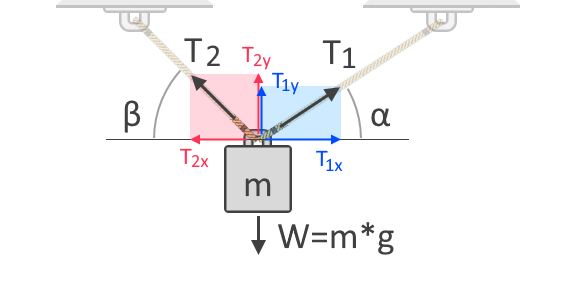
I det ovenfor viste fritekropsdiagram kan vi se de vandrette og lodrette komponenter af spændingskræfterne, T₁ og T₂. Kræfter er vektorer, hvilket betyder, at de altid har både størrelser og retninger. Ligesom alle vektorer kan kræfter udtrykkes i disse komponenter, hvilket giver kraftens indflydelse langs den vandrette og lodrette akse. T₁ₓ og T₂ₓ er de lodrette komponenter af henholdsvis T₁ og T₂. På den anden side er T₁ᵧ og T₂ᵧ henholdsvis de vertikale komponenter af de samme kræfter. Da tyngdekraften virker på genstanden i den lodrette akse, er vi nødt til at tage hensyn til spændingskræfternes lodrette komponenter i vores summering af kræfter på følgende måde:

ΣF = 0 = T₁ᵧ + T₂ᵧ + (-W)
W = T₁ᵧ + T₂ᵧ

Da vi også kender spændingskræfternes vinkler, kan vi ved hjælp af trigonometriske funktioner udtrykke T₁ᵧ og T₂ᵧ i udtryk for henholdsvis T₁ og T₂:

T₁ᵧ = T₁ * sin(α)
T₂ᵧ = T₂ * sin(β)
W = T₁ * sin(α) + T₂ * sin(β)

Vi kan også sige, at for at systemet er i ligevægt, må genstanden ikke bevæge sig vandret eller langs x-aksen. Derfor skal de horisontale komponenter af T₁ og T₂ så være lig med nul. Ved hjælp af trigonometri kan vi også udtrykke T₁ₓ og T₂ₓ i termer af henholdsvis T₁ og T₂:

T₁ₓ = T₂ₓ
T₁ * cos(α) = T₂ * cos(β)

Hvis vi dividerer begge sider med cos(α), får vi en ligning, hvor T₁ udtrykkes i termer af T₂ og vinklerne:

T₁ = T₂ * cos(β) / cos(α)

Vi kan derefter bruge denne ligning til at løse T₂ ved at indsætte T₂ * cos(β) / cos(α) som T₁ i vores ligning for summen af kræfter, som vist nedenfor:

W = T₁ * sin(α) + T₂ * sin(β)
W = T₂ * * sin(α) + T₂ * sin(β)
W = T₂ *
T₂ = W /

Endeligt, hvis vi multiplicerer hele denne ligning med cos(β) / cos(α), som vi afledte i værdien af T₁ i form af T₂, og derefter forenkler det hele, får vi denne ligning:

T₁ = W / *
T₁ = W / *
T₁ = W /

Nu skal man blot kende spændetrådenes vinkler i forhold til vandret. Hvis der er angivet en vinkel fra lodret, skal du blot trække denne vinkel fra 90°. Derved får du vinklen fra vandret. Hvis du imidlertid får andre værdier af vinkler, der kan være større end 90° eller endog 180°, kan du måske tjekke vores referencevinkelberegner for at hjælpe dig med at bestemme den vinkel, du har brug for. Efter at have bestemt værdierne for variablerne i vores spændingskraftformler kan vi nu løse for spændingskræfterne.